Table of Contents

अध्याय 9
किरण प्रकाशिकी एवं प्रकाशिक यंत्र
9.1 भूमिका
प्रकृति ने मानव नेत्र (दृष्टि पटल) को वैद्युतचुंबकीय स्पेक्ट्रम के एक छोटे परिसर में वैद्युत चुंबकीय तरंगों को सुग्राहिता सहित संसूचित कर सकने योग्य बनाया है| इस वैद्युतचुंबकीय स्पेक्ट्रम से संबंधित विकिरणों (तरंगदैर्घ्य लगभग 400 nm से 750 nm) को प्रकाश कहते हैं| मुख्य रूप से प्रकाश एवं दृष्टि की संवेदना के कारण ही हम अपने चारों ओर के संसार को समझते एवं उसकी व्याख्या करते हैं|
अपने सामान्य अनुभव से हम प्रकाश के विषय में अपनी अंतर्दृष्टि द्वारा दो बातों का उल्लेख कर सकते हैं| पहली, यह अत्यधिक तीव्र चाल से गमन करता है तथा, दूसरी, यह सरल रेखा में गमन करता है| इस तथ्य को पूर्ण रूप से समझने में लोगों को कुछ समय लगा कि प्रकाश की चाल (c) परिमित है तथा इसे मापा जा सकता है| वर्तमान में, इसका निर्वात में मान्य मान
c = 2.99792458 × 108 m s–1 है| अनेक प्रयोजनों के लिए, इसका मान c = 3 × 108 m s–1 पर्याप्त है| निर्वात में प्रकाश की चाल प्रकृति में प्राप्य उच्चतम चाल है|
हमारी अंतर्दर्शी धारणा कि प्रकाश सरल रेखा में गमन करता है, (जो कुछ हमने अध्याय 8 में सीखा था) का खंडन करती प्रतीत होती है क्योंकि वहाँ हमने प्रकाश को वैद्युतचुंबकीय तरंग माना था जिसकी तरंगदैर्घ्य स्पेक्ट्रम के दृश्य भाग में होती है| इन दोनों तथ्यों में सामंजस्य कैसे स्थापित किया जाए? इसका उत्तर यह है कि दैनिक जीवन की सामान्य वस्तुओं के साइज़ (व्यापक रूप में कुछ सेंटीमीटर की कोटि अथवा इससे अधिक) की तुलना में प्रकाश की तरंगदैर्घ्य काफ़ी कम होती है| जैसा कि आप अध्याय 10 में सीखेंगे, इस स्थिति में, प्रकाश तरंग को एक बिंदु से दूसरे बिंदु तक किसी सरल रेखा के अनुदिश गमन करते हुए माना जा सकता है| इस पथ को प्रकाश किरण कहते हैं तथा इसी प्रकार की किरणों के समूह से प्रकाश-पुंज बनता है|
इस अध्याय में, हम प्रकाश के किरण रूप का उपयोग करते हुए, प्रकाश के परावर्तन, अपवर्तन तथा विक्षेपण की परिघटनाओं के बारे में विचार करेंगे| परावर्तन तथा अपवर्तन के मूल नियमों का उपयोग करते हुए हम समतल तथा गोलीय परावर्ती एवं अपवर्ती पृष्ठों द्वारा प्रतिबिंबों की रचना का अध्ययन करेंगे| तत्पश्चात हम मानव नेत्र सहित कुछ महत्वपूर्ण प्रकाशिक यंत्रों की रचना एवं कार्य विधि का वर्णन करेंगे|
प्रकाश का कणिका मॉडल
न्यूटन का प्रकाश से संबंधित गहन प्रायोगिक कार्य एवं सैद्धांतिक अध्ययन प्रायः उनके गणित, यांत्रिकी तथा गुरुत्वाकर्षण से संबंधित मौलिक योगदानों को धुँधला कर देता है| उन्होंने प्रकाशिकी के क्षेत्र में पथ प्रदर्शक योगदान दिया| दकार्ते द्वारा प्रस्तुत कणिका मॉडल को उन्होंने और अधिक विकसित किया| इसमें यह माना गया कि प्रकाश ऊर्जा छोटे-छोटे कणों में संकेंद्रित होती है, जिसको उन्होंने कणिकाएँ कहा| न्यूटन ने प्रतिपादित किया कि प्रकाश ऊर्जा इन कणिकाओं में संकेंद्रित होती है| उन्होंने यह भी कल्पना की कि प्रकाश की कणिकाएँ द्रव्यमानरहित प्रत्यास्थ कण हैं| अपने यांत्रिकी के ज्ञान के आधार पर उन्होंने परावर्तन तथा अपवर्तन का सरल मॉडल प्रस्तुत किया| यह एक सामान्य प्रेक्षण है कि जब कोई गेंद किसी चिकने समतल पृष्ठ से टकराकर वापस लौटती है तो वह परावर्तन के नियमों का पालन करती है| जब यह टक्कर प्रत्यास्थ होती है तो वेग का परिमाण अपरिवर्तित रहता है| क्योंकि पृष्ठ चिकना है, पृष्ठ के समांतर कोई बल कार्य नहीं करता, अतः संवेग का इस दिशा में घटक भी अपरिवर्तित रहता है| केवल पृष्ठ के लंबवत घटक, अर्थात संवेग का अभिलंबवत घटक ही परावर्तन में उत्क्रमित हो जाता है| न्यूटन ने तर्क किया कि दर्पणों जैसे चिकने पृष्ठ कणिकाओं को इसी प्रकार परावर्तित करते हैं|
अपवर्तन की परिघटना की व्याख्या करने के लिए, न्यूटन ने अभिगृहीत प्रस्तुत किया कि कणिकाओं की चाल जल अथवा काँच में, वायु की अपेक्षा अधिक होती है| तथापि, बाद में यह ज्ञात हुआ कि प्रकाश की चाल जल अथवा काँच में वायु की अपेक्षा कम होती है|
प्रकाशिकी के क्षेत्र में, प्रयोगकर्ता के रूप में न्यूटन, सिद्धांतवादी न्यूटन की तुलना में कहीं अधिक दक्ष थे| उन्होंने कई एेसी परिघटनाओं का प्रेक्षण किया जिनको कणिकाओं के पदों में स्पष्ट कर पाना कठिन है| उदाहरण के लिए, जल के पृष्ठ पर तेल की पतली फ़िल्म के कारण विभिन्न वर्णों का प्रेक्षण| प्रकाश के आंशिक परावर्तन का गुण एेसा ही एक अन्य उदाहरण है| जब भी कोई तरण ताल (Swimming pool) के जल में देखता है, तब वह अपने चेहरे का प्रतिबिंब तो उसमें देखता ही है लेकिन साथ में ताल की पेंदी भी देखता है| न्यूटन ने तर्क किया कि जल के पृष्ठ पर आपतित कणिकाओं में से कुछ का परावर्तन होता है तथा कुछ पारगमित हो जाती हैं| परंतु दो प्रकार की कणिकाओं में भेद किस गुणधर्म के आधार पर किया जाए| न्यूटन को कुछ अप्रागुक्त, सांयोगिक परिघटनाओं की परिकल्पना करनी पड़ी जिनके द्वारा यह निश्चित किया जा सकता था कि कोई कणिका परावर्तित होगी अथवा नहीं| तथापि, अन्य परिघटनाओं की व्याख्या करने के लिए यह मानना पड़ा कि कणिकाएँ एेसे व्यवहार करती हैं जैसे कि वे सर्वसम हों| एेसी दुविधा प्रकाश के तरंग रूप में नहीं होती| कोई भी आने वाली तरंग वायु तथा जल की परिसीमा पर दो दुर्बल तरंगों में बँट सकती है|
9.2 गोलीय दर्पणों द्वारा प्रकाश का परावर्तन
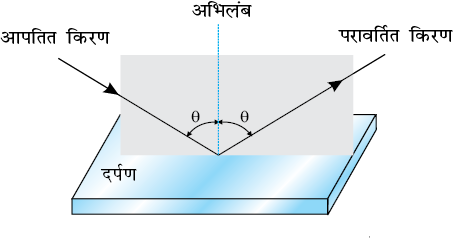
हम परावर्तन के नियमों से परिचित हैं| परावर्तन कोण (अर्थात, परावर्तित किरण तथा परावर्तक पृष्ठ अथवा दर्पण के आपतन बिंदु पर अभिलंब के बीच का कोण), आपतन कोण (आपतित किरण तथा दर्पण के आपतन बिंदु अभिलंब के बीच का कोण) के बराबर होता है| इसके अतिरिक्त, आपतित किरण, परावर्तित किरण तथा परावर्तक पृष्ठ के आपतन बिंदु पर अभिलंब एक ही समतल में होते हैं (चित्र 9.1)| ये नियम किसी भी परावर्तक पृष्ठ, चाहे वह समतल हो या वक्रित हो, के प्रत्येक बिंदु के लिए वैध हैं| तथापि, हम अपने विवेचन को वक्रित पृष्ठों की विशेष स्थिति, अर्थात गोलीय पृष्ठों तक ही सीमित रखेंगे| इस स्थिति में अभिलंब खींचने का तात्पर्य, पृष्ठ के आपतन बिंदु पर खींचे गए स्पर्शी पर लंब खींचना है| इसका अर्थ यह हुआ कि अभिलंब वक्रता त्रिज्या के अनुदिश अर्थात आपतन बिंदु को दर्पण के वक्रता केंद्र से मिलाने वाली रेखा पर है|
चित्र 9.1 आपतित किरण, परावर्तित किरण तथा परावर्तक पृष्ठ के आपतन बिंदु पर अभिलंब एक ही तल में होते हैं|
हम पहले ही अध्ययन कर चुके हैं कि गोलीय दर्पण का ज्यामितीय केंद्र इसका ध्रुव कहलाता है, जबकि गोलीय लेंस के ज्यामितीय केंद्र को प्रकाशिक केंद्र कहते हैं| गोलीय दर्पण के ध्रुव तथा वक्रता केंद्र को मिलाने वाली सरल रेखा मुख्य अक्ष कहलाती है| गोलीय लेंसों में जैसा कि आप बाद में देखेंगे, प्रकाशिक केंद्र को मुख्य फोकस से मिलाने वाली रेखा मुख्य अक्ष कहलाती है|
9.2.1 चिह्न परिपाटी
गोलीय दर्पणों द्वारा परावर्तन तथा गोलीय लेंसों द्वारा अपवर्तन के लिए प्रासंगिक सूत्र व्युत्पन्न करने के लिए, सर्वप्रथम हमें दूरियाँ मापने के लिए कोई चिह्न परिपाटी अपनानी होगी| इस पुस्तक में हम कार्तीय चिह्न परिपाटी (cartesian sign convention) का पालन करेंगे| इस परिपाटी के अनुसार वस्तु को दर्पण/लेंस के बायीं ओर रखते हैं तथा सभी दूरियाँ दर्पण के ध्रुव अथवा लेंस के प्रकाशिक केंद्र से मापी जाती हैं| आपतित प्रकाश की दिशा में मापी गई दूरियाँ धनात्मक मानी जाती हैं तथा जो दूरियाँ आपतित प्रकाश की दिशा के विपरीत दिशा में मापी जाती हैं वे ऋणात्मक मानी जाती हैं (चित्र 9.2)| x-अक्ष के सापेक्ष तथा दर्पण/लेंस के मुख्य अक्ष (x-अक्ष) के अभिलंबवत, उपरिमुखी मापित ऊँचाइयाँ धनात्मक मानी जाती हैं (चित्र 9.2)| अधोमुखी मापित ऊँचाइयों को ऋणात्मक लिया जाता है|

सामान्य मान्य परिपाटी के साथ हमें गोलीय दर्पणों के लिए एकल सूत्र तथा गोलीय लेंसों के लिए एकल सूत्र मिल जाते हैं तथा इन सूत्रों द्वारा हम विभिन्न स्थितियों का निपटान कर सकते हैं|
9.2.2 गोलीय दर्पणों की फोकस दूरी
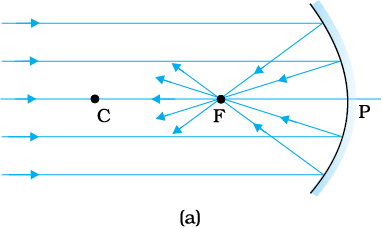
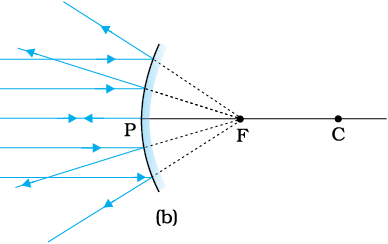
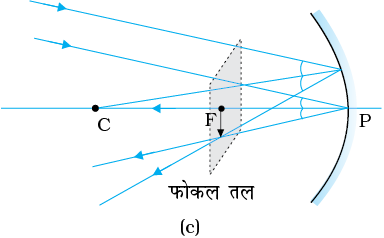
चित्र 9.3 में दर्शाया गया है कि जब कोई समांतर प्रकाश-पुंज किसी (a) अवतल दर्पण तथा (b) उत्तल दर्पण, पर आपतित होता है तो क्या होता है| हम यहाँ यह मानते हैं कि किरणें उपाक्षीय (paraxial) हैं, अर्थात वे दर्पण के ध्रुव P के निकट के बिंदुओं पर आपतित हैं तथा मुख्य अक्ष से छोटे कोण बनाती हैं| परावर्तित किरणें अवतल दर्पण के मुख्य अक्ष पर बिंदु F पर अभिसरित होती हैं [चित्र 9.3 (a)]| उत्तल दर्पण के लिए, परावर्तित किरणें इसके मुख्य अक्ष पर बिंदु F से अपसरित होती प्रतीत होती हैं [चित्र 9.3 (b)]| बिंदु F दर्पण का मुख्य फ़ोकस कहलाता है| यदि समांतर उपाक्षीय प्रकाश-पुंज अक्ष से कोई कोण बनाते हुए दर्पण पर आपतित होता है तो परावर्तित किरणें मुख्य अक्ष के बिंदु F से गुज़रने वाले तथा मुख्य अक्ष के अभिलंबवत तल के किसी बिंदु पर अभिसरित (अथवा उस बिंदु से अपसरित होती प्रतीत) होंगी| इस तल को दर्पण का फ़ोकस समतल कहते हैं [चित्र 9.3 (c)]|
दर्पण के फ़ोकस F तथा ध्रुव P के बीच की दूरी दर्पण की फ़ोकस दूरी कहलाती है तथा इसे f द्वारा निर्दिष्ट किया जाता है| अब हम यह दर्शाते हैं कि f = R/2, यहाँ R दर्पण की वक्रता त्रिज्या है| किसी आपतित प्रकाश किरण के परावर्तन की ज्यामिति चित्र 9.4 में दर्शायी गई है|
मान लीजिए C दर्पण का वक्रता केंद्र है| मुख्य अक्ष के समांतर एक प्रकाश किरण पर विचार कीजिए जो दर्पण से M पर टकराती है| तब CM बिंदु M पर दर्पण पर अभिलंब होगा| मान लीजिए θ आपतन कोण है तथा MD बिंदु M से मुख्य अक्ष पर लंब है| तब,
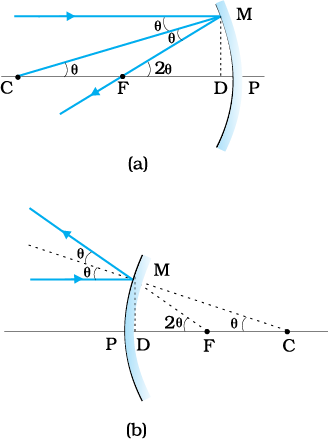
चित्र 9.4 (a) अवतल गोलीय दर्पण, तथा (b) उत्तल गोलीय दर्पण, पर किसी आपतित किरण के परावर्तन की ज्यामिति|
∠MCP = θ तथा ∠MFP = 2θ
अब, tanθ = तथा tan 2θ =
तथा tan 2θ =  (9.1)
(9.1)
θ के लघु मानों के लिए, जो कि उपाक्षीय किरणों के लिए सत्य है,
tanθ ≈ θ, tan 2θ ≈ 2θ
इसलिए समीकरण (9.1) से प्राप्त होता है
 = 2
= 2 
अथवा, FD = 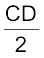 (9.2)
(9.2)
अथवा, θ के लघु मान के लिए, बिंदु D बिंदु P के बहुत निकट है| इसलिए, FD = f तथा CD = R | अतः समीकरण (9.2) से प्राप्त होता है
f = R/2 (9.3)
9.2.3 दर्पण समीकरण
यदि किसी बिंदु से आरंभ होकर प्रकाश किरणें परावर्तन तथा/अथवा अपवर्तन के पश्चात किसी अन्य बिंदु पर मिलती हैं तो वह बिंदु पहले बिंदु का प्रतिबिंब कहलाता है| यदि किरणें वास्तव में इस बिंदु पर अभिसरित होती हैं तो प्रतिबिंब वास्तविक होता है| इसके विपरीत, यदि किरणें वास्तव में नहीं मिलतीं, परंतु पीछे की ओर बढ़ाए जाने पर उस बिंदु से अपसरित होती प्रतीत होती हैं तो वह प्रतिबिंब आभासी होता है| इस प्रकार किसी वस्तु का परावर्तन तथा/अथवा अपवर्तन द्वारा स्थापित प्रतिबिंब उस वस्तु का बिंदु-दर-बिंदु तदनुरूप होता है|
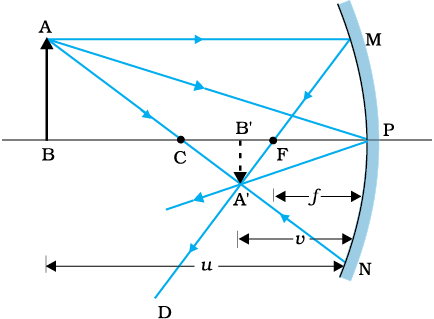
चित्र 9.5 किसी अवतल दर्पण द्वारा प्रतिबिंब रचना का किरण आरेख
सिद्धांत रूप में, हम वस्तु के किसी बिंदु से निकलने वाली कोई दो किरणें ले सकते हैं, उनके पथ अनुरेखित करते हैं, उनका प्रतिच्छेद बिंदु ज्ञात करते हैं और इस प्रकार, किसी गोलीय दर्पण द्वारा परावर्तन के कारण बना किसी बिंदु का प्रतिबिंब प्राप्त करते हैं| तथापि, व्यवहार में निम्नलिखित किरणों में से कोई सी दो किरणें लेना सुविधाजनक होता हैः
(i) किसी बिंदु से आने वाली वह किरण जो मुख्य अक्ष के समांतर है| परावर्तित किरण दर्पण के फ़ोकस से गुज़रती है|
(ii) वह किरण जो किसी अवतल दर्पण के वक्रता केंद्र से गुज़रती है अथवा उत्तल दर्पण के वक्रता केंद्र से जाती प्रतीत होती है| परावर्तित किरण केवल अपना पथ पुनः अनुरेखित करती है|
(iii) वह किरण जो किसी अवतल दर्पण के मुख्य फ़ोकस से गुज़रती है अथवा उत्तल दर्पण के मुख्य फ़ोकस से गुज़रती (की ओर दिष्ट) प्रतीत होती है| परावर्तित किरण मुख्य अक्ष के समांतर गमन करती है|
(iv) कोई किरण जो ध्रुव पर किसी भी कोण पर आपतित होती है| परावर्तित किरण, परावर्तन के नियमों का पालन करती है|
चित्र 9.5 बिंब के बिंदु A से निकलने वाली तीन किरणों को ध्यान में रखकर किरण-आरेख दर्शाता है| इसमें अवतल दर्पण द्वारा बनाया गया बिंब AB का प्रतिबिंब A′B′ (इस स्थिति में वास्तविक) दर्शाया गया है| इसका यह अर्थ नहीं है कि बिंदु A से केवल तीन किरणें ही निकलती हैं| किसी भी स्रोत से सभी दिशाओं में अनंत किरणें निकलती हैं| अतः यदि बिंदु A से निकलने वाली प्रत्येक किरण, अवतल दर्पण द्वारा परावर्तन के पश्चात बिंदु A′ से होकर गुज़रती है तो बिंदु A′ बिंदु A का वास्तविक प्रतिबिंब है|
अब हम दर्पण समीकरण अथवा बिंब दूरी (u), प्रतिबिंब दूरी (v) तथा फ़ोकस दूरी (f ) के बीच संबंध व्युत्पन्न करेंगे|
चित्र 9.5 से, दोनों समकोण त्रिभुज A′B′F तथा MPF समरूप हैं| (उपाक्षीय किरणों के लिए, MP को सरल रेखा CP के लंबवत माना जा सकता है|) अतः
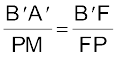
अथवा 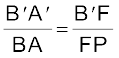 (Q PM = AB) (9.4)
(Q PM = AB) (9.4)
क्योंकि ∠ APB = ∠ A′PB′, समकोण त्रिभुज A′B′P तथा ABP भी समरूप हैं| अतः
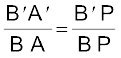 (9.5)
(9.5)
समीकरण (9.4) तथा (9.5) की तुलना करने पर हमें प्राप्त होगा
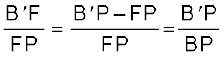 (9.6)
(9.6)
समीकरण (9.6) में दूरियों के परिमाण सम्मिलित हैं| अब हम चिह्न परिपाटी को लागू करते हैं| हम नोट करते हैं कि प्रकाश बिंब से दर्पण MPn की ओर गमन करता है| इस प्रकार इस दिशा को धनात्मक लिया जाता है| ध्रुव P से बिंब AB, प्रतिबिंब A′B′ तथा फ़ोकस F तक पहुँचने के लिए हमें आपतित प्रकाश की दिशा के विपरीत दिशा में गमन करना पड़ता है| इसलिए, इन तीनों के चिह्न ऋणात्मक होंगे| अतः
B′ P = –v, FP = –f, BP = –u
समीकरण (9.6) में इनका उपयोग करने पर प्राप्त होता है
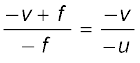
अथवा 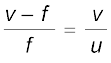
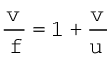
इसे v से भाग देने पर हमें प्राप्त होगा
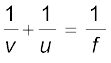 (9.7)
(9.7)
यह संबंध दर्पण समीकरण कहलाता है|
वस्तु के साइज़ के सापेक्ष प्रतिबिंब का साइज़ भी एक महत्वपूर्ण विचारणीय राशि है| हम किसी दर्पण के रैखिक आवर्धन (m) को प्रतिबिंब के साइज़ (h′) तथा बिंब के साइज़ (h) के अनुपात के रूप में परिभाषित करते हैं| अतः
m = 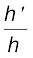 (9.8)
(9.8)
h तथा h′ को मान्य चिह्न परिपाटी के अनुसार धनात्मक अथवा ऋणात्मक लिया जाएगा| त्रिभुजों A′B′P तथा ABP, में हमें मिलता है,
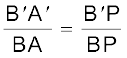
चिह्न परिपाटी लगाने पर, यह हो जाएगा

इस प्रकार
m = 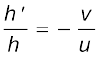 (9.9)
(9.9)
यहाँ पर हमने दर्पण समीकरण [समीकरण (9.7)] तथा आवर्धन सूत्र [समीकरण (9.9)] अवतल दर्पण द्वारा बने वास्तविक तथा उलटे प्रतिबिंब के लिए व्युत्पन्न किए हैं| परंतु वास्तव में उचित चिह्न परिपाटी का उपयोग करने पर, ये संबंध गोलीय दर्पणों (अवतल तथा उत्तल) द्वारा परावर्तन के सभी उदाहरणों (चाहे प्रतिबिंब वास्तविक बने या आभासी) पर लागू होते हैं| चित्र 9.6 में अवतल तथा उत्तल दर्पण द्वारा आभासी प्रतिबिबों की रचना के किरण-आरेख दर्शाए गए हैं| आप स्वयं यह सत्यापित कर सकते हैं कि समीकरण (9.7) तथा (9.9) इन उदाहरणों के लिए भी मान्य हैं|
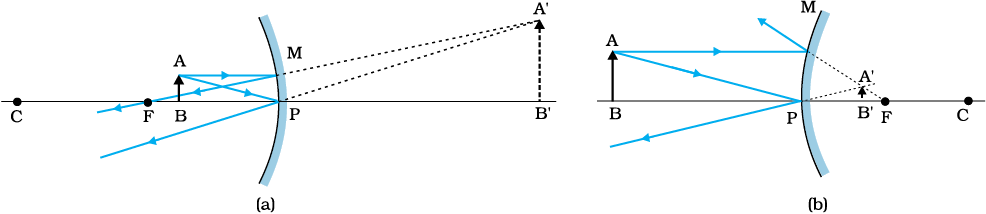
चित्र 9.6(a) अवतल दर्पण द्वारा प्रतिबिंब की रचना जबकि बिंब बिंदु P तथा F के बीच स्थित है, तथा (b) उत्तल दर्पण द्वारा प्रतिबिंब की रचना|
उदाहरण 9.1 मान लीजिए चित्र 9.5 में दर्शाए अवतल दर्पण के परावर्तक पृष्ठ के नीचे का आधा भाग किसी अपारदर्शी (अपरावर्ती) पदार्थ से ढक दिया गया है| दर्पण के सामने स्थित किसी बिंब के दर्पण द्वारा बने प्रतिबिंब पर इसका क्या प्रभाव पड़ेगा?
हल
आप सोच सकते हैं कि प्रतिबिंब में बिंब का आधा भाग दिखाई देगा| परंतु यह मानते हुए कि परावर्तन के नियम दर्पण के शेष भाग पर भी लागू होते हैं, अतः दर्पण द्वारा बिंब का पूर्ण प्रतिबिंब बनेगा| तथापि, क्योंकि परावर्ती पृष्ठ का क्षेत्रफल कम हो गया है| इसलिए प्रतिबिंब की तीव्रता कम हो जाएगी (इस उदाहरण में आधी)|
उदाहरण 9.2 किसी अवतल दर्पण के मुख्य अक्ष पर एक मोबाइल फोन रखा है| उचित किरण आरेख द्वारा प्रतिबिंब की रचना दर्शाइए| व्याख्या कीजिए कि आवर्धन एकसमान क्यों नहीं है| क्या प्रतिबिंब की विकृति दर्पण के सापेक्ष फोन की स्थिति पर निर्भर करती है?
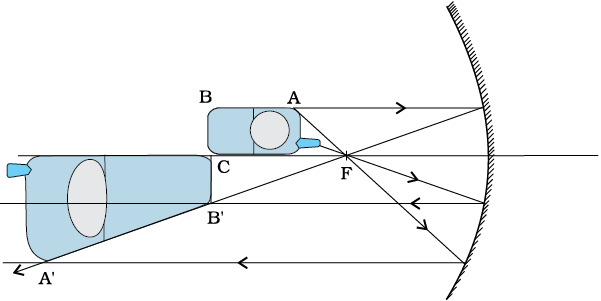
चित्र 9.7
हल
चित्र 9.7 में फ़ोन के प्रतिबिंब की रचना का प्रकाश-किरण आरेख दर्शाया गया है| मुख्य अक्ष के लंबवत समतल में स्थित भाग का प्रतिबिंब उसी समतल में होगा| यह उसी साइज़ का होगा, अर्थात B′C = BC| आप स्वयं ही पूर्ण रूप से समझ सकते हैं कि प्रतिबिंब में विकृति क्यों है?
उदाहरण 9.3 कोई वस्तु 15 cm वक्रता त्रिज्या के अवतल दर्पण से (i) 10 cm तथा (ii) 5 cm दूरी पर रखी है| प्रत्येक स्थिति में प्रतिबिंब की स्थिति, प्रकृति तथा आवर्धन परिकलित कीजिए|
हल
फोकस दूरी f = –15/2 cm = –7.5 cm
(i) बिंब दूरी u = –10 cm | तब समीकरण (9.7) से प्राप्त होगा
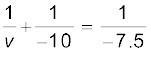
अथवा 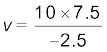 = – 30 cm
= – 30 cm
प्रतिबिंब बिंब की दिशा में दर्पण से 30 cm दूरी पर बनेगा|
आवर्धन m = 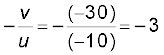
प्रतिबिंब आवर्धित, वास्तविक तथा उलटा है|
(ii) बिंब दूरी u = –5 cm तब समीकरण (9.7) से
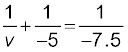
अथवा 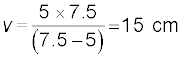
प्रतिबिंब दर्पण के पीछे 15 cm दूरी पर बनता है| यह प्रतिबिंब आभासी है|
आवर्धन m = 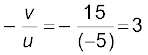
यह प्रतिबिंब आवर्धित, आभासी तथा सीधा है|
उदाहरण 9.4 मान लीजिए कि आप किसी स्थिर कार में बैठे हैं| आप 2 m वक्रता त्रिज्या के पार्श्व दृश्य दर्पण में किसी धावक को अपनी ओर आता हुआ देखते हैं| यदि धावक 5 m s-1 की चाल से दौड़ रहा हो, तो उसका प्रतिबिंब कितनी चाल से दौड़ता प्रतीत होगा जबकि धावक (a) 39 m, (b) 29 m, (c) 19 m, तथा (d) 9 m दूर है|
हल
दर्पण समीकरण (9.7), से हमें प्राप्त होता है

उत्तल दर्पण के लिए, क्योंकि R = 2 m, f = 1 m. तब
u = –39 m , 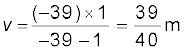
क्योंकि धावक 5 m s–1 की अपरिवर्ती चाल से चलता है, 1 s के पश्चात (u = –39 + 5 = –34 m) के लिए प्रतिबिंब की स्थिति v होगी (34/35 )m,
अतः 1 s में प्रतिबिंब की स्थिति में विस्थापन होगा

इसलिए जब धावक दर्पण से 39 m तथा 34 m के बीच में है, तो प्रतिबिंब की औसत चाल है (1/280) m s–1
इसी प्रकार यह देखा जा सकता है कि जब u = –29 m, –19 m तथा –9 m है तब जिस चाल से प्रतिबिंब गति करता प्रतीत होगा वह क्रमशः
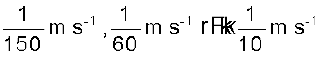 होंगी|
होंगी|
यद्यपि धावक एक अपरिवर्ती चाल से गतिमान है तथापि धावक दर्पण के जैसे-जैसे निकट आएगा उसके प्रतिबिंब की चाल में पर्याप्त वृद्धि प्रतीत होती जाएगी| यह परिघटना किसी स्थिर कार अथवा स्थिर बस में बैठा कोई भी व्यक्ति देख सकता है| यदि पीछे से आने वाला वाहन एक अपरिवर्ती चाल से लगातार पास आ रहा हो तो, चलते हुए वाहनों में इसी प्रकार की परिघटना देखी जा सकती है|
9.3 अपवर्तन
जब किसी पारदर्शी माध्यम में गमन करता कोई प्रकाश किरण-पुंज किसी दूसरे पारदर्शी माध्यम से टकराता है, तो प्रकाश का एक भाग पहले माध्यम में वापस परावर्तित हो जाता है| जबकि शेष भाग दूसरे माध्यम में प्रवेश करता है| हम प्रायः किसी किरण-पुंज को प्रकाश की किरण द्वारा निरूपित
करते हैं| जब कोई प्रकाश की किरण एक माध्यम से दूसरे माध्यम में तिर्यक आपतित (0°< i < 90°) होकर गमन करती है तो दोनों माध्यमों के अंतरापृष्ठ पर इसके संचरण की दिशा परिवर्तित हो जाती है| इस परिघटना को प्रकाश का अपवर्तन कहते हैं| स्नेल ने प्रयोगों द्वारा अपवर्तन के निम्नलिखित नियम प्रतिपादित किए|
(i) आपतित किरण, अपवर्तित किरण तथा अंतरापृष्ठ के आपतन बिंदु पर अभिलंब, एक ही समतल में होते हैं|
(ii) किन्हीं दो माध्यमों के युगल के लिए, आपतन कोण की ज्या (sine) तथा अपवर्तन कोण की ज्या का अनुपात एक स्थिरांक होता है|
याद रखिए, आपतन कोण (i ) तथा अपवर्तन कोण (r ) वे कोण हैं जो आपतित किरण तथा अपवर्तित किरण क्रमशः अभिलंब के साथ बनाती हैं| अतः
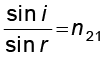 (9.10)
(9.10)
यहाँ n21 एक स्थिरांक है, जिसे पहले माध्यम के सापेक्ष दूसरे माध्यम का अपवर्तनांक कहते हैं| समीकरण (9.10) अपवर्तन के स्नेल के नियम के नाम से जानी जाती है| ध्यान देने योग्य बात यह है कि n21 दो माध्यम के युगल का अभिलक्षण है (तथा यह प्रकाश की तरंगदैर्घ्य पर भी निर्भर करता है), परंतु यह आपतन कोण पर निर्भर नहीं करता|
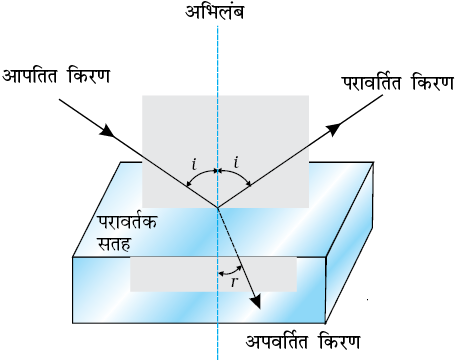
चित्र 9.8 प्रकाश का अपवर्तन तथा परावर्तन|
समीकरण (9.10) से यदि n21 > 1, r < i, अर्थात अपवर्तित किरण अभिलंब की ओर मुड़ जाती है| इस दशा में माध्यम 2 को माध्यम 1 की तुलना में प्रकाशतः सघन (अथवा संक्षेप में, सघन) माध्यम कहते हैं| इसके विपरीत यदि n21 <1, r > i, तो अपवर्तित किरण अभिलंब से दूर मुड़ती है| यह वह स्थिति है जिसमें आपतित किरण किसी सघन माध्यम से गमन करती हुई विरल माध्यम में अपवर्तित होती है|
नोट : प्रकाशिक घनत्व तथा द्रव्यमान घनत्व के बीच भ्रम उत्पन्न नहीं होना चाहिए| द्रव्यमान घनत्व एकांक आयतन का द्रव्यमान है| यह संभव है कि किसी प्रकाशिक सघन माध्यम का द्रव्यमान घनत्व प्रकाशिक विरल माध्यम के द्रव्यमान घनत्व से कम हो (प्रकाशिक घनत्व दो माध्यमों में प्रकाश की चाल का अनुपात है)| उदाहरण के लिए, तारपीन का तेल तथा जल| तारपीन के तेल का द्रव्यमान घनत्व जल के द्रव्यमान घनत्व से कम होता है| लेकिन इसका प्रकाशिक घनत्व अधिक होता है|
यदि n21 माध्यम 2 का माध्यम 1 के सापेक्ष अपवर्तनांक है तथा n12 माध्यम 1 का माध्यम 2 के सापेक्ष अपवर्तनांक है, तब यह स्पष्ट है कि
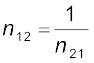 (9.11)
(9.11)
यदि n32 माध्यम 3 का माध्यम 2 के सापेक्ष अपवर्तनांक है तो यह भी स्पष्ट है कि n32 = n31 × n12, यहाँ n31 माध्यम 3 का माध्यम 1 के सापेक्ष अपवर्तनांक है|
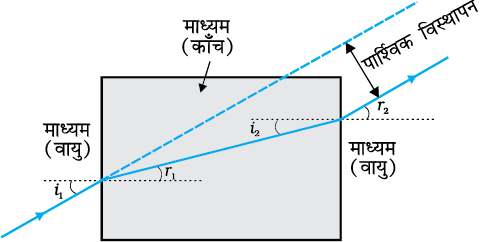
चित्र 9.9 समांतर फलकों के स्लैब से अपवर्तित किसी प्रकाश किरण का पाशि्ρवक विस्थापन|
अपवर्तन के नियमों पर आधारित कुछ प्रारंभिक परिणाम तुरंत प्राप्त किए जा सकते हैं| किसी आयताकार स्लैब में, अपवर्तन दो अंतरापृष्ठों पर होता है (वायु-काँच तथा काँच-वायु)| चित्र 9.9 द्वारा यह आसानी से देखा जा सकता है कि r2 = i1, अर्थात निर्गत किरण आपतित किरण के समांतर होती है–आपतित किरण के सापेक्ष निर्गत किरण में कोई विचलन नहीं होता, परंतु इसमें आपतित किरण के सापेक्ष पाशि्ρवक विस्थापन हो जाता है| एक दूसरा सुपरिचित प्रेक्षण यह भी है कि जल से भरे किसी तालाब की पेंदी ऊपर उठी प्रतीत होती है (चित्र 9.10)| अभिलंबवत दिशा के निकट से देखने पर यह दर्शाया जा सकता है कि आभासी गहराई (h1) वास्तविक गहराई (h2) को माध्यम (जल) के अपवर्तनांक से विभाजित करने पर प्राप्त होती है|
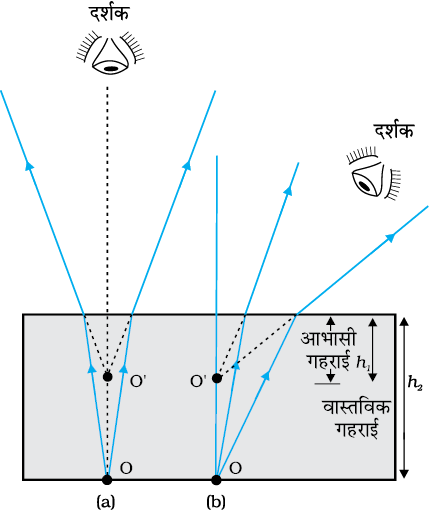
चित्र 9.10 (a) अभिलंबवत, तथा (b) तिर्यक दर्शन के लिए आभासी गहराई|
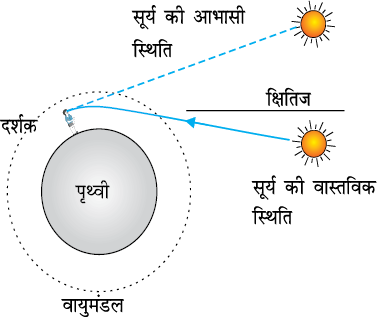
प्रकाश का वायुमंडलीय अपवर्तन अनेक रोचक परिघटनाएँ दर्शाता है| उदाहरण के लिए, प्रकाश के अपवर्तन के कारण ही सूर्य वास्तविक सूर्योदय से कुछ पहले दृष्टिगोचर होने लगता है तथा वास्तविक सूर्यास्त के कुछ समय पश्चात तक दृष्टिगोचर होता है (चित्र 9.11)| वास्तविक सूर्योदय से हमारा तात्पर्य है क्षितिज से सूर्य का ऊपर उठना| चित्र 9.11 में क्षितिज के सापेक्ष सूर्य की वास्तविक एवं आभासी स्थितियाँ दर्शायी गई हैं| चित्र में इस प्रभाव को समझने की दृष्टि से आवर्धित करके दर्शाया गया है| निर्वात के सापेक्ष वायु का अपवर्तनांक 1.00029 है| इसके कारण सूर्य की दिशा में लगभग आधे डिग्री (1/2°) का आभासी विस्थापन होता है जिसका वास्तविक सूर्यास्त तथा आभासी सूर्यास्त में तदनुरूपी अंतर लगभग 2 मिनट है| सूर्यास्त तथा सूर्योदय के समय सूर्य का आभासी चपटापन (अंडाकार आकृति) भी इसी परिघटना के कारण ही है|
उदाहरण 9.5 पृथ्वी अपने अक्ष पर एक घूर्णन करने में 24 h लेती है| सूर्य के सापेक्ष पृथ्वी से देखे जाने पर 1º विस्थापित होने में कितना समय लगता है?
हल
360° विस्थापित होने के लिए लिया गया समय = 24 h
1° विस्थापित होने के लिए लिया गया समय = (24/360) h = 4 min
डूबता हुआ बच्चा, जीवन रक्षक तथा स्नेल का नियम
चित्र में दर्शाए अनुसार एक आयताकार तरण ताल PQRS पर विचार करें| ताल के बाहर बिंदु G पर बैठा एक जीवन रक्षक एक बच्चे को बिंदु C पर डूबते हुए देखता है| रक्षक, बच्चे तक कम-से-कम समय में पहुँचना चाहता है| मान लीजिए G तथा C के बीच ताल का पार्श्व SR है| क्या उसको G तथा C के बीच सरल रेखीय पथ GAC को अपनाना चाहिए अथवा GBC को जिसमें जल में पथ BC सबसे छोटा होगा, या कोई अन्य पथ GXC? वह जानता है कि उसकी धरती पर दौड़ने की चाल v1 उसके तैरने की चाल v2 से अधिक है|
मान लीजिए जीवन रक्षक जल में बिंदु X पर प्रवेश करता है| मान लीजिए GX =l1 तथा XC =l2| तब G से C तक पहुँचने में लिया गया समय होगा
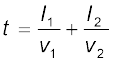
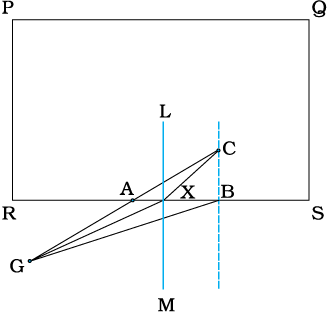
इस समय को न्यूनतम बनाने के लिए इसका ( X के निर्देशांक के सापेक्ष) अवकलन करना होगा तथा बिंदु X की उस स्थिति को ज्ञात करना होगा ताकि t का मान न्यूनतम हो| ये समस्त परिकलन करने पर (जिसे हम यहाँ पर छोड़ रहे हैं) हमें ज्ञात होता है कि रक्षक को जल में उस बिंदु पर प्रवेश करना चाहिए जहाँ स्नेल का नियम संतुष्ट होता है| इसे समझने के लिए SR के बिंदु X पर एक लंब LM खींचिए| मान लीजिए ∠GXM = i तथा ∠CXL = r| तब हम देख सकते हैं कि t न्यूनतम होगा जब
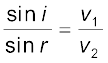
प्रकाश के लिए v1/v2, निर्वात में प्रकाश का वेग तथा माध्यम में प्रकाश के वेग का अनुपात, माध्यम का अपवर्तनांक n है|
संक्षेप में, चाहे तरंग हो या कण अथवा कोई मनुष्य, जब भी दो माध्यम तथा दो वेग सम्मिलित होते हैं तो न्यूनतम समय के लिए स्नेल के नियम को अपनाना आवश्यक है|
9.4 पूर्ण आंतरिक परावर्तन
जब प्रकाश किसी प्रकाशतः सघन माध्यम से प्रकाशतः विरल माध्यम में गमन करता है, तब अंतरापृष्ठ पर वह अंशतः वापस उसी माध्यम में परावर्तित हो जाता है तथा अंशतः दूसरे माध्यम में अपवर्तित हो जाता है| इस परावर्तन को आंतरिक परावर्तन कहते हैं|
जब कोई प्रकाश किरण सघन माध्यम से विरल माध्यम में प्रवेश करती है तो यह अभिलंब से दूर मुड़ जाती है, उदाहरणार्थ, चित्र 9.12 में किरण AO1B आपतित किरण AO1 अंशतः परावर्तित (O1C) तथा अंशतः पारगमित अथवा अपवर्तित (O1B) होती है, तथा अपवर्तन कोण (r) आपतन कोण (i) से अधिक होता है| जैसे-जैसे आपतन कोण में वृद्धि होती है, अपवर्तन कोण में भी वृद्धि होती है, जब तक कि किरण AO3 के लिए अपवर्तन कोण का मान π/2 (90°) हो जाए| अपवर्तित किरण अभिलंब से इतनी अधिक मुड़ जाती है कि वह दोनों माध्यमों के अंतरापृष्ठ को छूने लगती है| इसे चित्र 9.12 में किरण AO3D द्वारा दर्शाया गया है| यदि आपतन कोण में इससे अधिक वृद्धि की जाती है (उदाहरण के लिए किरण AO4) तो अपवर्तन संभव नहीं होता तथा आपतित किरण पूर्णतः परावर्तित हो जाती है| इसे पूर्ण आंतरिक परावर्तन कहते हैं| जब किसी पृष्ठ द्वारा प्रकाश परावर्तित होता है तो सामान्यतः इसका कुछ भाग पारगमित हो जाता है| इसलिए परावर्तक पृष्ठ चाहे जितना भी चिकना क्यों न हो, परावर्तित किरण सदैव आपतित किरण से कम तीव्रता की होती है| दूसरी ओर पूर्ण आंतरिक परावर्तन में प्रकाश का कोई पारगमन नहीं होता|
वह आपतन कोण जिसका तदनुरूपी अपवर्तन कोण 90º होता है, जैसे ∠AO3N, दिए हुए माध्यमों के युगल के लिए क्रांतिक कोण (ic ) कहलाता है| स्नेल के नियम [समीकरण (9.10)] के अनुसार हम देखते हैं कि यदि अपवर्तक माध्यम का आपेक्षिक अपवर्तनांक एक से कम है, तो क्योंकि sin r का अधिकतम मान एक होता है, अतः sin i के मान की कोई ऊपरी सीमा है जिस तक यह नियम लागू किया जा सकता है| यह है i = ic इस प्रकार
sin ic = n21 (9.12)
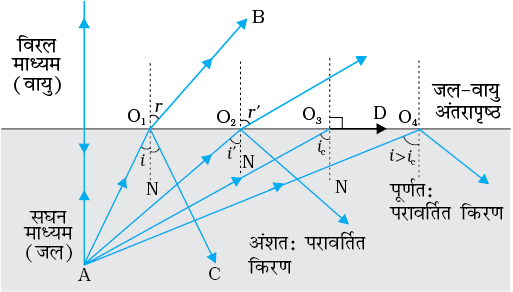
चित्र 9.12 सघन माध्यम (जल) तथा विरल माध्यम (वायु) के अंतरापृष्ठ पर बिंदु A (सघन माध्यम में) से विभिन्न कोणों पर आपतित किरणों का अपवर्तन तथा पूर्ण आंतरिक परावर्तन|
i के ic से अधिक मानों के लिए स्नेल के अपवर्तन के नियम को लागू नहीं किया जा सकता, अतः कोई अपवर्तन संभव नहीं होता|
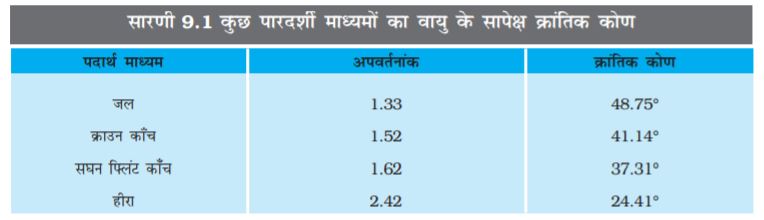
सघन माध्यम 1 का विरल माध्यम 2 के सापेक्ष अपवर्तनांक होगा n12 = 1/sin ic| सारणी 9.1 में कुछ प्ररूपी क्रांतिक कोणों को सूचीबद्ध किया गया है|
पूर्ण आंतरिक परावर्तन के लिए एक प्रदर्शन
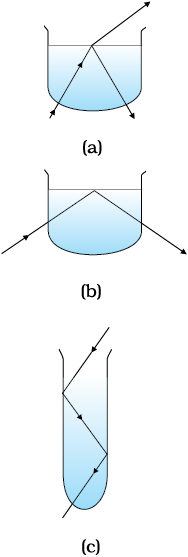
सभी प्रकाशिक परिघटनाओं को आजकल आसानी से उपलब्ध लेसर टॉर्च या संकेतक का प्रयोग करके बड़ी सरलता से प्रदर्शित किया जा सकता है| एक काँच का बीकर लीजिए जिसमें स्वच्छ जल भरा हो| जल में दूध या किसी अन्य निलंबन की कुछ बूँदें मिलाकर हिलाइए जिससे जल थोड़ा आविल हो जाए| एक लेसर संकेतक लीजिए और इसके किरण-पुंज को आविल जल से गुज़ारिए| आप देखेंगे कि जल के अंदर किरण-पुंज का पथ चमकीला दिखाई देता है|
किरण-पुंज को बीकर के नीचे से इस प्रकार डालिए कि यह दूसरे सिरे पर जल के ऊपरी पृष्ठ पर टकराए| क्या आप देख पाते हैं कि इसमें आंशिक परावर्तन (जो मेज़ के नीचे एक बिंदु के रूप में दिखाई देगा) तथा आंशिक अपवर्तन (जो वायु में निकलकर छत पर एक बिंदु के रूप में दिखाई देता है) होता है [चित्र 9.13 (a)] ? अब लेसर किरण-पुंज को बीकर के एक ओर से इस प्रकार डालिए कि यह जल के ऊपरी पृष्ठ पर तिर्यक टकराए [चित्र 9.13 (b)]| लेसर किरण-पुंज की दिशा को इस प्रकार समायोजित कीजिए कि आपको एेसा कोण प्राप्त हो जाए जिससे जल के पृष्ठ के ऊपर अपवर्तन पूर्ण रूप से समाप्त हो जाए तथा किरण-पुंज पूर्ण रूप से जल में वापस परावर्तित हो जाए| यह सरलतम रूप में पूर्ण आंतरिक परावर्तन है|
इस जल को एक लंबी परखनली में उलटिए तथा लेसर प्रकाश को इसके ऊपर से डालिए जैसा कि चित्र 9.13 (c) में दर्शाया गया है| लेसर किरण-पुंज की दिशा को इस प्रकार समायोजित कीजिए कि प्रत्येक बार जब यह परखनली की दीवारों से टकराए तो इसका पूर्ण आंतरिक परावर्तन हो| यह दृश्य एेसा ही है जैसा कि प्रकाशिक तंतुओं में होता है|
ध्यान रखिए कि लेसर किरण-पुंज में कभी भी सीधा न देखें और न ही इसे किसी के चेहरे पर डालें|
9.4.1 प्रकृति में पूर्ण आंतरिक परावर्तन तथा इसके प्रौद्योगिकीय अनुप्रयोग
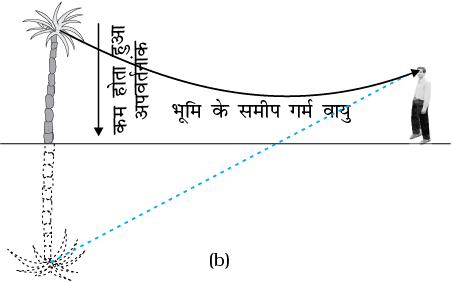
(i) मरीचिका : गर्मियों के गर्म दिनों में पृथ्वी के निकट की वायु अपने से ऊपर की वायु की तुलना में अधिक गर्म हो जाती है| वायु का अपवर्तनांक घनत्व के साथ बढ़ जाता है| गर्म वायु कम सघन होती है तथा उसका अपवर्तनांक ठंडी वायु की तुलना में कम होता है| यदि वायु प्रवाह धीमा है, अर्थात, वायु शांत है तो वायु की विभिन्न परतों का प्रकाशिक घनत्व ऊँचाई के साथ बढ़ता है| परिणामस्वरूप, किसी ऊँची वस्तु, जैसे किसी पेड़ से आता हुआ प्रकाश एेसे माध्यम में गमन करता है जिसका अपवर्तनांक भूमिपृष्ठ की ओर घटता जाता है| अतः इस प्रकार की वस्तु से आने वाली प्रकाश की किरण उत्तरोत्तर अभिलंब से दूर मुड़ती जाती है और यदि भूमिपृष्ठ के पास की वायु के लिए आपतन कोण क्रांतिक कोण से अधिक हो जाए तो यह पूर्ण आंतरिक परावर्तित होती है| इसे चित्र 9.14 में दर्शाया गया है| दूरस्थ प्रेक्षक के लिए, प्रकाश भूमिपृष्ठ के कहीं नीचे से आता हुआ प्रतीत होता है| प्रेक्षक स्वाभाविक रूप से यही मान लेता है कि यह प्रकाश भूमिपृष्ठ से ही, जैसे, ऊँची वस्तु के समीप जल से भरे किसी तालाब या पोखर से परावर्तित होकर उस तक पहुँच रहा है| किसी दूरस्थ वस्तु का इस प्रकार बना उलटा प्रतिबिंब दृष्टिभ्रम उत्पन्न करता है| इस परिघटना को मरीचिका कहते हैं| इस प्रकार की मरीचिका तप्त मरुस्थलों में अत्यंत सामान्य है| गर्मियों के दिनों में, किसी बस या कार में चलते समय सड़क पर, विशेष रूप से महामार्गों पर, सड़क का दूर का कोई भाग गीला प्रतीत होता है| लेकिन जब आप उस स्थान पर पहुँचते हैं, तो आपको गीलेपन का कोई प्रमाण नहीं मिलता| यह भी मरीचिका के कारण है|
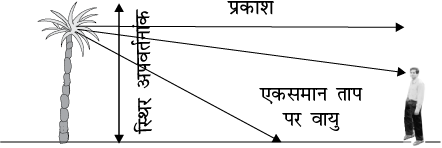
(a)
(ii) हीरा : हीरे अपनी भव्य चमक के लिए प्रसिद्ध हैं| इनकी चमक मुख्य रूप से उनके भीतर प्रकाश के पूर्ण आंतरिक परावर्तन के कारण है| हीरे-वायु अंतरापृष्ठ के लिए क्रांतिक कोण (≅24.4°) का मान बहुत कम है| इसलिए यदि एक बार हीरे में प्रकाश प्रवेश कर जाए तो इसके अंदर प्रकाश के पूर्ण आंतरिक परावर्तन होने की अत्यधिक संभावनाएँ होती हैं| प्रकृति में पाए जाने वाले विरले हीरे ही अपनी सर्वविदित चमक दर्शाते हैं| हीरे की चमक-दमक हीरा तराशने वाले कारीगरों की तकनीकी दक्षता पर निर्भर होती है| किसी हीरे को उचित प्रकार से काटकर उसके भीतर बहुल आंतरिक परावर्तन कराए जा सकते हैं|
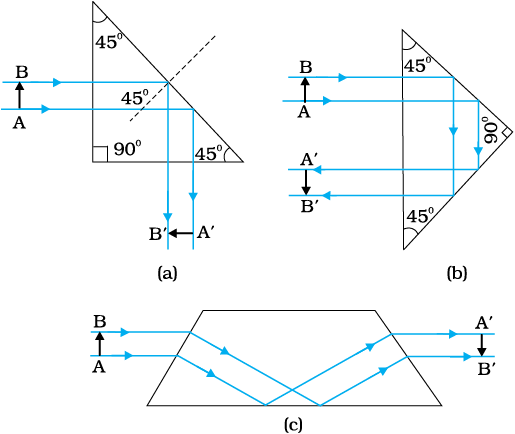
चित्र 9.15 किरणों को π/2 तथा π पर मोड़ने के लिए या प्रतिबिंब के साइज़ में परिवर्तन किए बगैर उलटने के लिए डिज़ाइन किए गए प्रिज्मों में पूर्ण आंतरिक परावर्तन का उपयोग किया जाता है|
(iii) प्रिज़्म : प्रकाश को 90º अथवा 180º पर मोड़ने के लिए डिज़ाइन किए गए प्रिज्मों में पूर्ण आंतरिक परावर्तन का उपयोग किया जाता है [चित्र 9.15 (a) तथा (b)]| एेसे प्रिज़्म को प्रतिबिंब के साइज़ में बिना कोई परिवर्तन किए उलटने के लिए भी प्रयोग किया जाता है [चित्र 9.15 (c)]| पहली दो स्थितियों के लिए, प्रिज़्म के पदार्थ के क्रांतिक कोण ic को 45º से कम होना चाहिए| सारणी 9.1 देखने पर हम यह पाते हैं कि दोनों ही प्रकार के काँच क्राउन तथा फ़्लिंट के लिए यह सत्य है|
(iv) प्रकाशिक तंतु : आजकल प्रकाशिक तंतुओं का, श्रव्य तथा दृश्य संकेतों को लंबी दूरी तक संचरित करने के लिए व्यापक रूप से उपयोग किया जाता है| प्रकाशिक तंतुओं में भी पूर्ण आंतरिक परावर्तन की परिघटना का उपयोग किया जाता है| प्रकाशिक तंतु उच्च गुणता के संयुक्त काँच/क्वाट्ज़ तंतुओं से रचित किया जाता है| प्रत्येक तंतु में एक क्रोड (core) तथा आच्छद (cladding) होता है| क्रोड के पदार्थ का अपवर्तनांक आच्छद के अपवर्तनांक की तुलना में अधिक होता है|
जब प्रकाश के रूप में कोई संकेत उचित कोण पर तंतु के एक सिरे पर दिष्ट होता है तब यह उसकी लंबाई के अनुदिश बार-बार पूर्ण आंतरिक परावर्तित होता है तथा अंततः दूसरे सिरे से बाहर निकल आता है (चित्र 9.16)| क्योंकि प्रत्येक चरण में प्रकाश का पूर्ण आंतरिक परावर्तन होता है इसलिए प्रकाश संकेत की तीव्रता में कोई विशेष हानि नहीं होती| प्रकाश तंतु इस प्रकार बनाए जाते हैं कि एक ओर के आंतरिक पृष्ठ पर परावर्तित होने के पश्चात दूसरे पृष्ठ पर प्रकाश क्रांतिक कोण से अधिक कोण पर आपतित होता है| यहाँ तक कि तंतु में मुड़ाव होने पर भी प्रकाश तंतु के भीतर उसकी लंबाई के अनुदिश सरलतापूर्वक गमन कर सकता है| इस प्रकार एक प्रकाश तंतु प्रकाशित पाइप (लाइट पाइप) के रूप में प्रयोग किया जा सकता है|
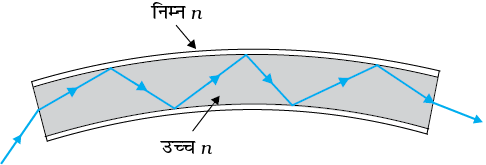
चित्र 9.16 जब प्रकाश किसी प्रकाशिक तंतु में चलता है तो इसका क्रमिक पूर्ण आंतरिक परावर्तन होता है|
प्रकाशिक तंतुओं के बंडल (गुच्छ) का कई प्रकार से उपयोग किया जा सकता है| प्रकाशिक तंतुओं का बड़े पैमाने पर वैद्युत संकेतों, जिन्हें उचित ट्रांसड्यूरों द्वारा प्रकाश में परिवर्तित कर लेते हैं, के प्रेषण तथा अभिग्रहण में उपयोग किया जाता है| स्पष्ट है कि प्रकाशिक तंतुओं का उपयोग प्रकाशिक संकेत प्रेषण के लिए भी किया जा सकता है| उदाहरण के लिए, इन्हें आंतरिक अंगों; जैसे– ग्रसिका, आमाशय तथा आंत्रों के दृश्य अवलोकन के लिए ‘लाइट पाइप’ के रूप में प्रयोग किया जाता है| आपने सामान्य रूप से उपलब्ध महीन प्लास्टिक तंतुओं से बने सजावटी लैंप देखे होंगे| इन प्लास्टिक के तंतुओं के स्वतंत्र सिरे एक फव्वारे जैसी संरचना बनाते हैं| इन तंतुओं का दूसरा सिरा एक विद्युत लैंप के ऊपर जुड़ा होता है| जब लैंप के स्विच को ‘अॉन’ करते हैं, तो प्रकाश प्रत्येक तंतु के नीचे से चलता हुआ इसके स्वतंत्र सिरे की नोक पर एक प्रकाश बिंदु के रूप में दिखाई देता है| इस प्रकार के सजावटी लैंपों के तंतु प्रकाशिक तंतु हैं|
प्रकाशिक तंतुओं के निर्माण में प्रमुख आवश्यकता यह है कि इनके भीतर लंबी दूरियाँ तय करते समय प्रकाश का अवशोषण बहुत कम होना चाहिए| इसे क्वाट्ρज़ जैसे पदार्थों के शोधन तथा विशिष्ट विरचन द्वारा बनाया जाता है| सिलिका काँच तंतुओं में 1 km लंबे तंतु में प्रकाश के 95% से भी अधिक भाग को संचरित करना संभव है| (इसकी तुलना 1 km मोटाई के खिड़की के काँच के ब्लॉक में जितने प्रतिशत प्रकाश के संचरण की आप अपेक्षा करते हैं, से कीजिए|)
9.5 गोलीय पृष्ठों तथा लेंसों द्वारा अपवर्तन
अब तक हमने समतल अंतरापृष्ठों पर अपवर्तन के विषय में विचार किया है| अब हम दो पारदर्शी माध्यमों के गोलीय अंतरापृष्ठों पर अपवर्तन के विषय में विचार करेंगे| किसी गोलीय पृष्ठ के अत्यंत सूक्ष्म भाग को समतलीय माना जा सकता है तथा उसके पृष्ठ के प्रत्येक बिंदु पर समान अपवर्तन के नियमों का अनुप्रयोग किया जा सकता है| गोलीय दर्पण द्वारा परावर्तन की ही भाँति आपतन बिंदु पर अभिलंब पृष्ठ के उस बिंदु पर स्पर्शी तल के लंबवत होता है, तथा वह इसीलिए पृष्ठ के वक्रता केंद्र से गुज़रता है| हम पहले एकल गोलीय पृष्ठ द्वारा अपवर्तन पर विचार करेंगे तथा इसके पश्चात पतले लेंसों की चर्चा करेंगे| कोई पतला लेंस दो गोलीय पृष्ठों से घिरा पारदर्शी माध्यम होता है; जिसका कम से कम एक पृष्ठ अवश्य गोलीय होना चाहिए| एक गोलीय पृष्ठ द्वारा निर्मित प्रतिबिंब के लिए सूत्र का अनुप्रयोग, किसी लेंस के दो पृष्ठों पर, क्रमिक रूप में करके हम पतले लेंसों के लिए लेंस मेकर सूत्र तथा उसके पश्चात लेंस सूत्र प्राप्त करेंगे|
9.5.1 किसी गोलीय पृष्ठ पर अपवर्तन
चित्र 9.17 में वक्रता त्रिज्या R तथा वक्रता केंद्र C के गोलीय पृष्ठ के मुख्य अक्ष पर स्थित किसी वस्तु के बिंदु O के प्रतिबिंब I की रचना की ज्यामिति दर्शायी गई है| प्रकाश किरणें n1 अपवर्तनांक के किसी माध्यम से आपतित होकर n2 अपवर्तनांक के किसी अन्य माध्यम में जाती हैं| पहले की भाँति, हम पृष्ठ का द्वारक (अथवा पार्श्व साइज़) अन्य संबद्ध दूरियों की तुलना में काफ़ी छोटा लेते हैं ताकि आवश्यकतानुसार लघु कोण सन्निकटन किया जा सके| विशेष रूप से हम NM को N से मुख्य अक्ष पर लंब की लंबाई के लगभग बराबर लेंगे| यहाँ पर
tan ∠NOM = 
tan ∠NCM = 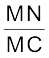
tan ∠NIM = 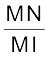
अब ∆NOC के लिए, i बहिर्कोण है| अतः
i = ∠NOM + ∠NCM
प्रकाश स्रोत तथा प्रकाशमिति
यह सर्वविदित है कि परमशून्य ताप से ऊपर रखी वस्तुएँ वैद्युत चुंबकीय विकिरण उत्सर्जित कर सकती हैं| जिस तरंगदैर्घ्य परिसर में वस्तुएँ विकिरण उत्सर्जित करेंगी वह इसके परम ताप पर निर्भर करता है| किसी तप्तपिंड द्वारा उत्सर्जित विकिरण, उदाहरण के लिए, कोई टंग्स्टेन तंतु लैंप जिसका ताप 2850 K है, आंशिक रूप से अदृश्य हैं तथा मुख्यतः अवरक्त (अथवा ऊष्मा) भाग में हैं| जैसे-जैसे पिंड का ताप बढ़ता है, इसके द्वारा उत्सर्जित विकिरण दृश्य भाग में आ जाते हैं| सूर्य जिसके पृष्ठ का ताप लगभग 5500 K है, विकिरण उत्सर्जित करता है| इसकी ऊर्जा का तरंगदैर्घ्य के फलन के रूप में खींचा गया ग्राफ़ λ = 550 nm पर एक शिखर दर्शाता है जो हरे वर्ण के संगत है तथा लगभग दृश्य क्षेत्र के मध्य में है| किसी दिए गए पिंड का ऊर्जा-तरंगदैर्घ्य वितरण ग्राफ़ किसी तरंगदैर्घ्य पर शिखर दर्शाता है जो कि उस पिंड के परम ताप के व्युत्क्रमानुपाती होता है|
मानव नेत्र द्वारा अनुभव किए गए प्रकाश की माप प्रकाशमिति कहलाती है| प्रकाशमिति शरीर क्रियात्मक परिघटना की माप है जो मानव नेत्र द्वारा प्रकाश का उद्दीपन और जिसका दृक तंत्रिका (optic nerves) द्वारा संचरण तथा मस्तिष्क द्वारा विश्लेषण होता है| प्रकाशमिति की तीन प्रमुख भौतिक राशियाँ – (i) स्रोत की ज्योति तीव्रता, (ii) स्रोत से प्रवाहित प्रकाश अथवा ज्योति फ्लक्स, तथा (iii) पृष्ठ का प्रदीप्त घनत्व हैं| ज्योति तीव्रता (I) का SI मात्रक कैंडेला (cd) है| कैंडेला किसी दिशा में ज्योति की वह तीव्रता है जो540 × 1012 Hz आवृत्ति के एकवर्णीय विकिरण के स्रोत से उत्सर्जित होती हो तथा उसी दिशा में जिसकी विकिरण तीव्रता (1/683) वाट प्रति स्टेरेडियन हो| यदि कोई प्रकाश स्रोत एक स्टेरेडियन के घन कोण में एक कैंडेला ज्योति तीव्रता का प्रकाश उत्सर्जित करता है तो उस घन कोण में उत्सर्जित कुल ज्योति फ्लक्स एक ल्यूमेन (lm) होता है| 100 वाट का मानक ताप दीप्त प्रकाश बल्ब लगभग 1700 ल्यूमेन उत्सर्जित करता है|
प्रकाशमिति में प्रदीप्ति घनत्व ही एकमात्र एेसा प्राचल है जिसे सीधा मापा जा सकता है| इसे किसी पृष्ठ के इकाई क्षेत्रफल पर आपतित ज्योति फ्लक्स (lm/m2 अथवा लक्स) द्वारा परिभाषित किया जाता है| अधिकांश प्रकाशमापी इस भौतिक राशि को मापते हैं| किसी I ज्योति तीव्रता के स्रोत द्वारा उत्पन्न प्रदीप्ति घनत्व का E = I/r2 द्वारा व्यक्त किया जाता है| यहाँ r पृष्ठ से स्रोत के बीच की लंबवत दूरी है| उत्सर्जी अथवा परावर्ती चपटे पृष्ठों की द्युति (brightness) के अभिलक्षणों को दर्शाने के लिए एक भौतिक राशि जिसे ज्योतिर्मयता (L) कहते हैं, का उपयोग करते हैं| इसका मात्रकcd/m2 है (जिसे उद्योग में 'nit' भी कहते हैं| किसी अच्छे LCD कंप्यूटर मॉनीटर की द्युति लगभग 250 nits होती है|
i = 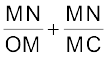 (9.13)
(9.13)
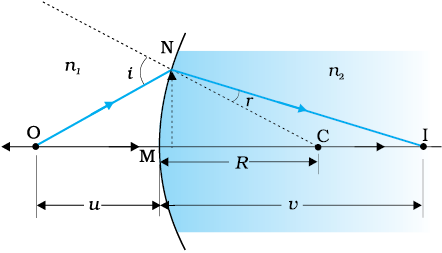
चित्र 9.17 दो माध्यमों को पृथक करने वाले किसी गोलीय पृष्ठ पर अपवर्तन|
इसी प्रकार
r = ∠NCM – ∠NIM
अर्थात r = 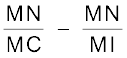 (9.14)
(9.14)
अब स्नेल के नियम के अनुसार
n1 sin i = n2 sin r
अथवा कोणों के छोटे मानों के लिए
n1i = n2r
समीकरणों (9.13) तथा (9.14) से i तथा r के मान रखने पर हमें प्राप्त होता है
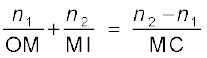 (9.15)
(9.15)
यहाँ OM, MI तथा MC दूरियों के परिमाणों को निरूपित करते हैं| कार्तीय चिह्न परिपाटी का अनुप्रयोग करने पर,
OM = –u, MI = +v, MC = +R
इनका मान समीकरण (9.15) में रखने पर हमें प्राप्त होता है,
 (9.16)
(9.16)
समीकरण (9.16) से हमें बिंब तथा प्रतिबिंब के बीच में माध्यम के अपवर्तनांक तथा गोलीय वक्रित पृष्ठ की वक्रता त्रिज्या के पदों के रूप में संबंध प्राप्त होता है| समीकरण (9.16) किसी भी प्रकार के वक्रित गोलीय पृष्ठ के लिए मान्य है|
उदाहरण 9.6 वायु में रखे किसी बिंदु स्रोत से प्रकाश काँच के किसी गोलीय पृष्ठ पर पड़ता है| (n = 1.5 तथा वक्रता त्रिज्या = 20 cm)| प्रकाश स्रोत की काँच के पृष्ठ से दूरी 100 cm है| प्रतिबिंब कहाँ बनेगा?
हल
यहाँ पर, समीकरण (9.16) में दिए सूत्र में
u = – 100 cm, v = ?, R = + 20 cm, n1 = 1, तथा n2 = 1.5 रखने पर
हमें प्राप्त होता है
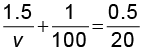
अथवा v = +100 cm
प्रतिबिंब आपतित प्रकाश की दिशा में काँच के पृष्ठ से 100 cm की दूरी पर बनेगा|
9.5.2 किसी लेंस द्वारा अपवर्तन
चित्र 9.18 (a) में किसी उभयोत्तल लेंस द्वारा प्रतिबिंब-रचना की ज्यामिति दर्शायी गई है| इस प्रतिबिंब की रचना को दो चरणों में देखा जा सकता है : (i) पहला अपवर्ती पृष्ठ बिंब O का प्रतिबिंब I1 बनाता है [चित्र 9.18 (b)]| प्रतिबिंब I1 दूसरे पृष्ठ द्वारा प्रतिबिंब I बनने के लिए आभासी बिंब की भाँति कार्य करता है [चित्र 9.18 (c)]| समीकरण (9.15) का उपयोग पहले अंतरापृष्ठ ABC पर करने पर हमें प्राप्त होता है :
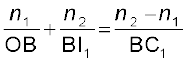 (9.17)
(9.17)
दूसरे अंतरापृष्ठ* ADC के लिए भी समान प्रक्रिया का अनुप्रयोग करने पर हमें प्राप्त होता है :
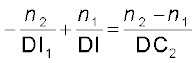 (9.18)
(9.18)
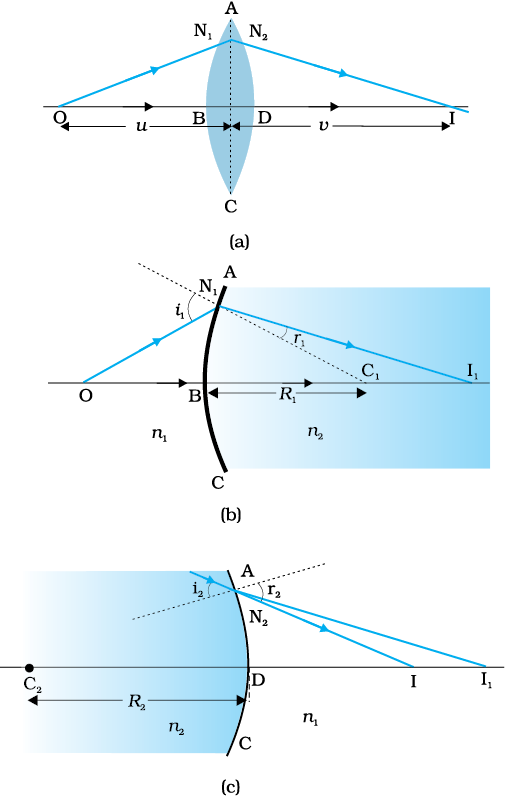
किसी पतले लेंस के लिए BI1 = DI1| समीकरणों (9.17) तथा (9.18) को जोड़ने पर हमें प्राप्त होता है :
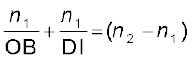
 (9.19)
(9.19)
मान लीजिए बिंब अनंत पर है तो, OB → ∞ तथा
DI = f, तब समीकरण (9.19) से प्राप्त होगा :
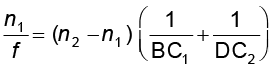 (9.20)
(9.20)
वह बिंदु जहाँ अनंत पर रखे बिंब का प्रतिबिंब बनता है, लेंस का फ़ोकस F कहलाता है तथा दूरी f द्वारा इसकी फ़ोकस दूरी प्राप्त होती है| किसी लेंस के इसके दोनों ओर दो फ़ोकस होते हैं F तथा F’| चिह्न परिपाटी द्वारा
BC1 = + R1 [चित्र 9.18(b)]
DC2 = –R2 [चित्र 9.18(c)]
इसलिए समीकरण (9.20) को लिखा जा सकता है :
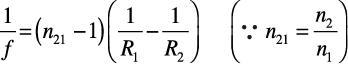 (9.21)
(9.21)
समीकरण (9.21) को लेंस-मेकर सूत्र के रूप में जाना जाता है| स्पष्ट रूप से यह सूत्र उचित वक्रता त्रिज्याओं के पृष्ठों के उपयोग द्वारा वांछित फोकस दूरी के लेंसों की अभिकल्पना (डिज़ाइन) करने में उपयोगी है| ध्यान देने योग्य बात यह है कि यही सूत्र अवतल लेंसों पर भी समान रूप से लागू होता है| उस स्थिति में R1ऋणात्मक तथा R2 धनात्मक होता है, इसलिए f ऋणात्मक होता है|
समीकरण (9.19) तथा (9.20) से हमें प्राप्त होता है :
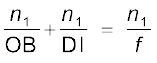 (9.22)
(9.22)
पुनः पतले लेंस-सन्निकटन में बिंदु B तथा D दोनों ही लेंस के प्रकाशिक केंद्र के बहुत निकट माने जाते हैं| चिह्न परिपाटी का उपयोग करने पर BO = – u, DI = +v| इन मानों को (9.22) में रखने पर हमें प्राप्त होता है
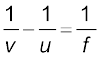 (9.23)
(9.23)
समीकरण (9.23) लेंसों के लिए परिचित पतले लेंस सूत्र है| यद्यपि यहाँ हमने इसे उत्तल लेंस द्वारा निर्मित वास्तविक प्रतिबिंब के लिए व्युत्पन्न किया है, तथापि यह सूत्र दोनों ही लेंसों अर्थात, उत्तल तथा अवतल तथा दोनों ही प्रकार के प्रतिबिंबों, वास्तविक तथा आभासी के लिए मान्य है|
यह बताना आवश्यक है कि किसी उभयोत्तल अथवा उभयावतल लेंस के दो फ़ोकस F तथा F′ लेंस के प्रकाशिक केंद्र से समान दूरी पर हैं| प्रकाश के स्रोत की ओर स्थित फ़ोकस को प्रथम फ़ोकस बिंदु कहते हैं जबकि दूसरा द्वितीय फ़ोकस बिंदु कहलाता है|
लेंसों द्वारा बने किसी बिंब के प्रतिबिंब की स्थिति ज्ञात करने के लिए सिद्धांत रूप में हम बिंब के किसी बिंदु से आने वाली कोई भी दो किरणें लेकर तथा अपवर्तन के नियमों द्वारा उनके पथ अनुरेखित करके उस बिंदु की स्थिति ज्ञात करते हैं, जहाँ अपवर्तित किरणें वास्तव में मिलती हैं (अथवा मिलती प्रतीत होती हैं)| तथापि, व्यवहार में निम्नलिखित में से कोई सी दो किरणों का चयन करना कार्य को सहज बना देता है|
(i) बिंब से निकलने वाली वह किरण जो लेंस के मुख्य अक्ष के समांतर होती है, अपवर्तन के पश्चात (उत्तल लेंस में) लेंस के दूसरे मुख्य फ़ोकस F′ से गुज़रती है, अथवा (अवतल लेंस में) लेंस के प्रथम मुख्य फ़ोकस F से अपसरित प्रतीत होती है|
(ii) लेंस के प्रकाशिक केंद्र से गुज़रने वाली प्रकाश किरण अपवर्तन के पश्चात् बिना किसी विचलन के निर्गत होती है|
(iii) (a) किसी उत्तल लेंस के प्रथम मुख्य से होकर गुज़रने वाली कोई प्रकाश की किरण अपवर्तन के पश्चात् मुख्य अक्ष के समांतर गमन करती है| [चित्र 9.19(a)]
(b) किसी अवतल लेंस पर उसके द्वितीय बिंदु की ओर आती प्रतीत होती हुई कोई प्रकाश की किरण अपवर्तन के पश्चात् मुख्य अक्ष के समांतर गमन करती है| [चित्र 9.19(b)]
चित्र 9.19 (a) तथा (b) में इन नियमों को क्रमशः उत्तल तथा अवतल लेंसों के लिए दर्शाया गया है| आपको लेंस से विभिन्न दूरियों पर बिंब को रखकर इस प्रकार के किरण आरेख खींचने का अभ्यास करना चाहिए तथा यह भी सत्यापित करना चाहिए कि लेंस सूत्र, समीकरण (9.23), सभी उदाहरणों में समान रूप से लागू होता है|
यहाँ पर यह अवश्य याद रखना चाहिए कि किसी बिंब के प्रत्येक बिंदु से अनंत किरणें उत्सर्जित होती हैं| ये सभी किरणें लेंस से अपवर्तन के पश्चात एक ही प्रतिबिंब बिंदु से गुज़रती हैं|
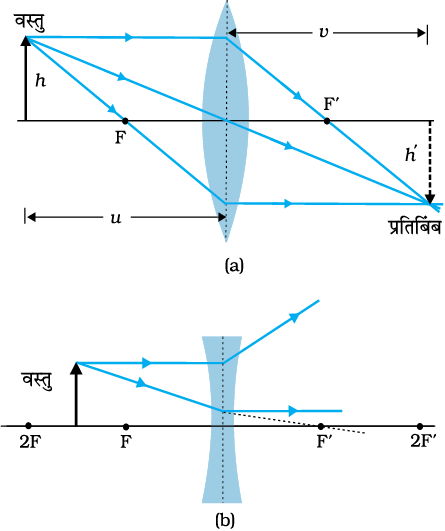
चित्र 9.19 (a) उत्तल लेंस, (b) अवतल लेंस से गुज़रने वाली प्रकाश किरणों का अनुरेखण|
दर्पण की भाँति लेंसों के लिए भी, किसी लेंस द्वारा उत्पन्न आवर्धन (m) को प्रतिबिंब के साइज़ (h′ ) तथा बिंब के साइज़ (h) के अनुपात के रूप में परिभाषित किया जाता है| गोलीय दर्पणों की भाँति यहाँ भी किसी लेंस के लिए यह सरलता से देखा जा सकता है कि
m = 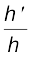 =
= 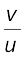 (9.24)
(9.24)
चिह्न परिपाटी का पालन करने पर हम यह पाते हैं कि उत्तल अथवा अवतल लेंस द्वारा बने सीधे (तथा आभासी) प्रतिबिंब के लिए m धनात्मक होता है, जबकि किसी उलटे (तथा वास्तविक) प्रतिबिंब के लिए m ऋणात्मक होता है|
उदाहरण 9.7 कोई जादूगर खेल दिखाते समय n = 1.47 अपवर्तनांक के काँच के लेंस को किसी द्रव से भरी द्रोणिका में डालकर अदृश्य कर देता है| द्रव का अपवर्तनांक क्या है? क्या यह द्रव जल हो सकता है?
हल
द्रव में लेंस के अदृश्य होने के लिए द्रव का अपवर्तनांक, लेंस के काँच के अपवर्तनांक के बराबर होना चाहिए; n1 =n2| अर्थात द्रव का अपवर्तनांक 1.47 है| इस प्रकरण में 1/f =0 या f → ∞ प्राप्त होगा| द्रव के अंदर लेंस काँच की एक समतल शीट की भाँति कार्य करेगा| द्रोणिका में भरा द्रव जल (अपवर्तनांक = 1.33) नहीं हो सकता| यह द्रव ग्लिसरीन हो सकता है|
9.5.3 लेंस की क्षमता
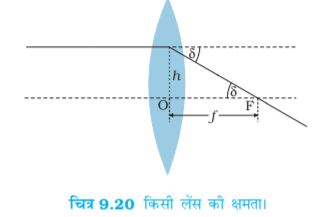
किसी लेंस की क्षमता उस पर पड़ने वाले प्रकाश को अभिसरित अथवा अपसरित करने की कोटि की माप होती है| स्पष्टतः कम फ़ोकस दूरी का कोई लेंस आपतित प्रकाश को अधिक मोड़ता है, उत्तल लेंस में अपवर्तित किरण अभिसरित होती है तथा अवतल लेंस में अपवर्तित किरण अपसरित होती है| किसी लेंस की क्षमता P को उस कोण की स्पर्शज्या से परिभाषित करते हैं, जिससे यह किसी मुख्य अक्ष के समांतर प्रकाश पुंज को जो प्रकाशिक केंद्र से एकांक दूरी पर आकर गिरता है, अभिसरित या अपसरित करता है| (चित्र 9.20)|
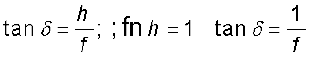
अथवा 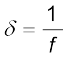 (δ के लघु मान के लिए)|
(δ के लघु मान के लिए)|
अतः P = 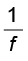 (9.25)
(9.25)
लेंस की क्षमता का SI मात्रक डाइअॉप्टर (D) : 1D = 1m–1 है| अतः 1m फोकस दूरी के लेंस की क्षमता एक डाइअॉप्टर है| अभिसारी लेंसों की क्षमता धनात्मक तथा अपसारी लेंस की क्षमता ऋणात्मक होती है| इस प्रकार जब कोई नेत्र चिकित्सक + 2.5 D क्षमता का संशोधक लेंस निर्धारित करता है, तब + 40 cm फ़ोकस दूरी के उत्तल लेंस की आवश्यकता होती है| – 4.0 D क्षमता के लेंस से तात्पर्य – 25 cm फ़ोकस दूरी का अवतल लेंस होता है|
उदाहरण 9.8 (i) यदि f = +0.5 m है तो लेंस की क्षमता क्या है? (ii) किसी उभयोत्तल लेंस के दो फलकों की वक्रता त्रिज्याएँ 10 cm तथा 15 cm हैं| उसकी फ़ोकस दूरी 12 cm है| लेंस के काँच का अपवर्तनांक ज्ञात कीजिए| (iii) किसी उत्तल लेंस की वायु में फ़ोकस दूरी 20 cm है| जल में इसकी फ़ोकस दूरी क्या है? [वायु-जल का अपवर्तनांक 1.33 तथा वायु-काँच का अपवर्तनांक 1.5 है|]
हल
(i) लेंस की क्षमता = +2D
(ii) यहाँ f = +12 cm, R1 = +10 cm, R2 = –15 cm
वायु का अपवर्तनांक 1 माना जाता है|
समीकरण (9.22) के लेंस सूत्र का प्रयोग करने के लिए f, R1 तथा R2 के लिए चिह्न परिपाटी के अनुसार विभिन्न राशियों के मान रखने पर हमें

n = 1.5 प्राप्त होगा|
(iii) वायु में काँच के लेंस के लिए, n2 = 1.5, n1 = 1, f = +20 cm
इस प्रकार लेंस सूत्र से प्राप्त होगा
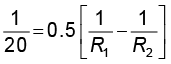
उसी काँच के लेंस के लिए जल में, n2 = 1.5, n1 = 1.33. इसलिए
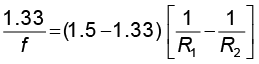 (9.26)
(9.26)
इन दोनों समीकरणों को संयोजित करने पर हमें मिलेगा
f = + 78.2 cm
9.5.4 संपर्क में रख पतले लेंसों का संयोजन
एक-दूसरे के संपर्क में रखे f1 तथा f2 फ़ोकस दूरियों के दो पतले लेंसों A तथा B पर विचार कीजिए| मान लीजिए कोई बिंब पहले लेंस A के फ़ोकस से दूर किसी बिंदु O पर स्थित है (चित्र 9.21)| पहला लेंस बिंदु I1 पर प्रतिबिंब बनाता है| क्योंकि प्रतिबिंब I1 वास्तविक है, अतः यह दूसरे लेंस B के लिए आभासी बिंब की भाँति कार्य करता है तथा अंतिम प्रतिबिंब I पर बनता है| हमें इस बात को समझ लेना चाहिए कि पहले लेंस से प्रतिबिंब का बनना, केवल अंतिम प्रतिबिंब की स्थिति निर्धारित करने के लिए, माना गया है| वास्तव में पहले लेंस से निकलने वाली किरणों की दिशा, उनके दूसरे लेंस से टकराने वाले कोण के अनुसार परिवर्तित हो जाती है| क्योंकि लेंस पतले हैं, हम दोनों लेंसों के प्रकाशिक केंद्रों को संपाती मान सकते हैं| मान लीजिए यह केंद्रीय बिंदु P द्वारा निर्दिष्ट होता है|
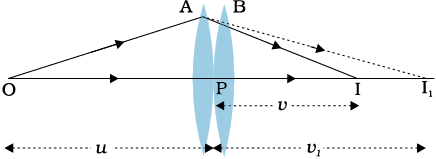
चित्र 9.21 संपर्क में रखे दो पतले लेंसों द्वारा प्रतिबिंब बनना|
पहले लेंस A द्वारा बने प्रतिबिंब के लिए
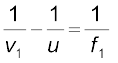 (9.27)
(9.27)
दूसरे लेंस B द्वारा बने प्रतिबिंब के लिए
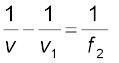 (9.28)
(9.28)
समीकरण (9.27) तथा (9.28) को जोड़ने पर,
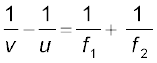 (9.29)
(9.29)
इन दो लेंसों के तंत्र को f फ़ोकस दूरी के किसी एकल लेंस के तुल्य मानने पर,
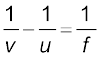
अर्थात
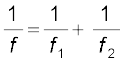 (9.30)
(9.30)
यह व्युत्पत्ति संपर्क में रखे कई पतले लेंसों के निकाय के लिए भी मान्य है| यदि f1, f2, f3,... फ़ोकस दूरियों के बहुत से लेंस एक-दूसरे के संपर्क में रखे हैं, तो इस संयोजन की प्रभावी फ़ोकस दूरी होगी :
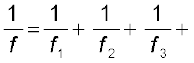 … (9.31)
… (9.31)
क्षमता के पदों में समीकरण (9.31) को इस प्रकार भी लिखा जा सकता है
P = P1 + P2 + P3 + … (9.32)
यहाँ P इस लेंस संयोजन की नेट क्षमता है| ध्यान दीजिए, समीकरण (9.32) में अलग-अलग क्षमताओं का बीजगणितीय योग दिया गया है, अर्थात समीकरण के दक्षिण पक्ष में कुछ पद धनात्मक (उत्तल लेंसों के लिए) तथा कुछ पद ऋणात्मक (अवतल लेंसों के लिए) हो सकते हैं| लेंसों के संयोजन हमें व्युत्पन्न आवर्धन क्षमता के अपसारित अथवा अभिसारित लेंस प्राप्त करने में सहायक होते हैं तथा ये प्रतिबिंब की तीक्ष्णता में भी वृद्धि कर देते हैं| क्योंकि पहले लेंस द्वारा बना प्रतिबिंब दूसरे लेंस के लिए बिंब बन जाता है, समीकरण (9.25) में यह अंतर्निहित है कि संयोजन का कुल आवर्धन m, अलग-अलग आवर्धनों (m1, m2, m3,..) के गुणनफल के बराबर होता है|
m = m1 m2 m3 ... (9.33)
इस प्रकार के लेंसों के संयोजन सामान्यतः कैमरों, सूक्ष्मदर्शियों, दूरबीनों तथा अन्य प्रकाशिक यंत्रों के लेंसों के डिज़ाइन में उपयोग किए जाते हैं|
उदाहरण 9.9 चित्र 9.22 में दिए गए लेंसों के संयोजन द्वारा निर्मित प्रतिबिंब की स्थिति ज्ञात कीजिए|

चित्र 9.22
हल पहले लेंस द्वारा निर्मित प्रतिबिंब
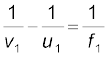

अथवा v1 = 15 cm
पहले लेंस द्वारा निर्मित प्रतिबिंब दूसरे लेंस के लिए बिंब की भाँति कार्य करता है| यह दूसरे लेंस के दायीं ओर (15 – 5)cm = 10 cm दूरी पर है| यद्यपि प्रतिबिंब वास्तविक है परंतु यह दूसरे लेंस के लिए आभासी बिंब का कार्य करता है| अर्थात इससे दूसरे लेंस के लिए किरणें आती हुई प्रतीत होती हैं|
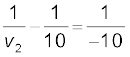
या v2 = ∞
यह आभासी प्रतिबिंब दूसरे लेंस के बायीं ओर अनंत दूरी पर बनता है| यह तीसरे लेंस के लिए बिंब की भाँति कार्य करता है|
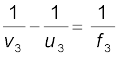
अथवा 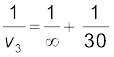
या v3 = 30 cm
अंतिम प्रतिबिंब तीसरे लेंस के दायीं ओर 30 cm दूरी पर बनता है|
9.6 प्रिज़्म में अपवर्तन
चित्र 9.23 में किसी प्रिज़्म ABC से प्रकाश किरण को गुज़रते हुए दर्शाया गया है| पहले फलक AB पर आपतन कोण तथा अपवर्तन कोण क्रमशः i तथा r1 हैं, जबकि दूसरे फलक (काँच से वायु में) AC पर आपतन कोण r2 तथा अपवर्तन कोण या निर्गत कोण e हैं| निर्गत किरण RS तथा आपतित किरण की दिशा PQ के बीच के कोण को विचलन कोण δ कहते हैं|
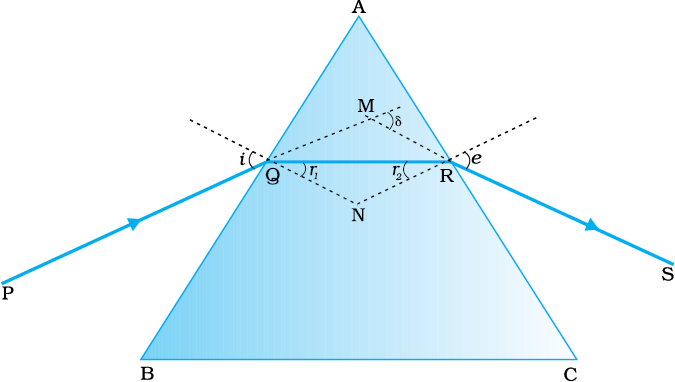
चित्र 9.23 काँच के त्रिभुजाकार प्रिज़्म से किसी प्रकाश किरण का गुज़रना|
चतुर्भुज AQNR में दो कोण (Q तथा R शीर्षों पर) समकोण हैं| इसलिए इस भुजा के अन्य दो कोणों का योग 180º है|
∠A + ∠QNR = 180º
त्रिभुज QNR से
r1 + r2 + ∠QNR = 180º
इन दोनों समीकरणों की तुलना करने पर, हमें प्राप्त होगा
r1 + r2 = A (9.34)
कुल विचलन δ दोनों फलकों पर विचलनों का योग हैः
δ = (i – r1 ) + (e – r2 )
अर्थात, δ = i + e – A
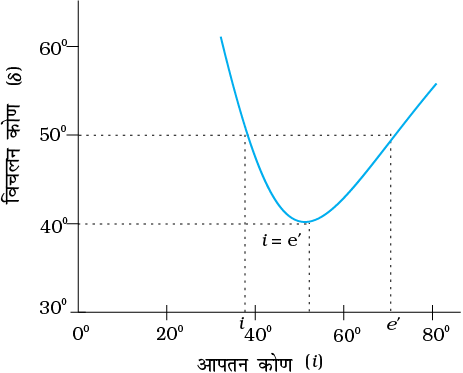
इस प्रकार विचलन कोण आपतन कोण पर निर्भर करता है| चित्र 9.24 में आपतन कोण तथा विचलन कोण के बीच ग्राफ़ दर्शाया गया है| आप यह देख सकते हैं कि व्यापक रूप से, केवल i = e को छोड़कर, प्रत्येक विचलन कोण δ के तदनुरूपी i के तथा इस प्रकार e के दो मान हैं| यह तथ्य समीकरण (9.35) में i तथा e की सममिति से अपेक्षित है, अर्थात, यदि i तथा e को आपस में बदल दिया जाए तो δ अपरिवर्तित रहता है| भौतिक रूप में यह इस तथ्य से संबंधित है कि चित्र 9.23 में प्रकाश किरण के पथ को वापस आरेखित करने पर वही विचलन कोण प्राप्त होता है| न्यूनतम विचलन Dm पर, प्रिज़्म के अंदर अपवर्तित किरण इसके आधार के समांतर हो जाती है| हमें प्राप्त होता है
δ = Dm, i = e जिसका तात्पर्य है कि r1 = r2
समीकरण (9.34) से हमें प्राप्त होता है
2r = A अथवा r = 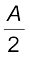 (9.36)
(9.36)
इसी प्रकार समीकरण (9.35) से हमें प्राप्त होता है
Dm = 2i – A, अथवा i = (A + Dm)/2 (9.37)
यदि प्रिज़्म के पदार्थ का अपवर्तनांक n21 है तो
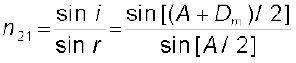 (9.38)
(9.38)
कोण A तथा Dm की माप प्रयोग द्वारा की जा सकती है| इस प्रकार समीकरण (9.38) प्रिज़्म के पदार्थ के अपवर्तनांक के मापन की विधि है|
छोटे कोण के प्रिज़्म अर्थात पहले प्रिज़्म के लिए Dm भी काफ़ी छोटा होता है तथा हमें प्राप्त होगा
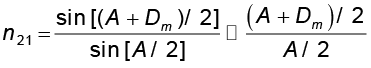
Dm = (n21–1)A
इसका तात्पर्य है कि पतले प्रिज़्म में प्रकाश का विचलन काफ़ी कम होता है|
9.7 सूर्य के प्रकाश के कारण कुछ प्राकृतिक परिघटनाएँ
हमारे चारों ओर की वस्तुओं के साथ प्रकाश के खेल हमें बहुत-सी रमणीय परिघटनाएँ देते हैं| हमारे चारों ओर हर समय दिखाई देने वाले भव्य रंग सूर्य के प्रकाश के कारण ही संभव हैं|
प्रिज़्म द्वारा दृश्य (अथवा श्वेत) प्रकाश के परिक्षेपण (कक्षा-X) तथा वैद्युतचुंबकीय स्पेक्ट्रम (अध्याय 8, कक्षा-XII) के बारे में पढ़ते समय हमें ज्ञात हो चुका है कि प्रकाश का वर्ण प्रकाश की आवृत्ति अथवा माध्यम में तरंगदैर्घ्य से संबंद्ध होता है| दृश्य स्पेक्ट्रम में लाल प्रकाश दीर्घ तरंगदैर्घ्य के सिरे (~750 nm) पर जबकि बैंगनी प्रकाश लघु तरंगदैर्घ्य के सिरे (~400 nm) पर होता है|
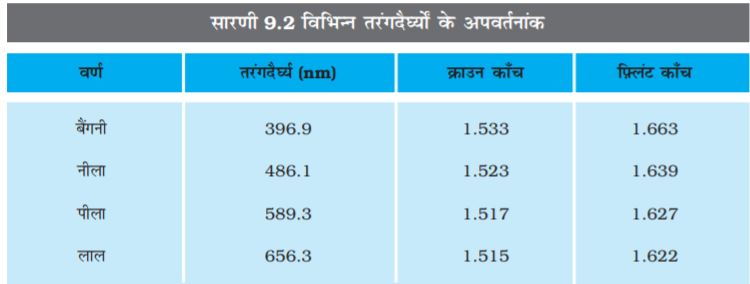
परिक्षेपण का कारण यह है कि किसी माध्यम का अपवर्तनांक विभिन्न तरंगदैर्घ्यों (वर्णों) के लिए भिन्न-भिन्न होता है| उदाहरण के लिए, श्वेत प्रकाश का लाल घटक सबसे कम मुड़ता है जबकि बैंगनी घटक अधिक मुड़ता है| तुल्य रूप में हम कह सकते हैं कि काँच के प्रिज़्म में बैंगनी प्रकाश की तुलना में लाल प्रकाश अपेक्षाकृत अधिक चाल से गमन करता है|
सारणी 9.2 में विभिन्न तरंगदैर्घ्यों के लिए क्राउन काँच तथा फ्लिंट काँच के अपवर्तनांक दर्शाए गए हैं| मोटे लेंसों को अनेक प्रिज़्मों से मिलकर बना हुआ माना जा सकता है, इसलिए मोटे लेंस प्रकाश के परिक्षेपण के कारण वर्ण विपथन (chromatic abberation) दर्शाते हैं| जब श्वेत प्रकाश मोटे लेंसों से होकर गुज़रता है तो लाल एवं बैंगनी वर्ण अलग-अलग बिंदुओं पर फ़ोकस होते हैं| इस परिघटना को वर्ण विपथन कहते हैं|
आवृत्ति के साथ अपवर्तनांक में परिवर्तन कुछ माध्यमों में अन्य माध्यमों की तुलना में अधिक सुस्पष्ट होता है| वास्तव में, निर्वात में प्रकाश की चाल तरंगदैर्घ्य पर निर्भर नहीं करती| अतः निर्वात (अथवा सन्निकटतः वायु) एक अपरिक्षेपी माध्यम है जिसमें सभी वर्ण समान चाल से गमन करते हैं| यह इस तथ्य से भी सिद्ध होता है कि सूर्य का प्रकाश हमारे पास तक श्वेत प्रकाश के रूप में पहुँचता है, इसके विभिन्न संघटकों के रूप में नहीं| इसके विपरीत काँच एक परिक्षेपी माध्यम है|
आकाश का नीला प्रतीत होना, श्वेत बादल, सूर्योदय तथा सूर्यास्त के समय आकाश की लालिमा, इंद्रधनुष, कुछ पक्षियों के पंखो, सीपियों, शंखों एवं मोतियों की रंग-बिरंगी चमक कुछ एेसे अद्भुत एवं आश्चर्यजनक प्राकृतिक चमत्कार हैं, जिससे हम भली-भाँति परिचित हैं और उनके अभ्यस्त हो चुके हैं| यहाँ इनमें से कुछ का हम भौतिकी की दृष्टि से वर्णन करेंगे|
9.7.1 इंद्रधनुष
इंद्रधनुष वायुमंडल में उपस्थित जल की बूँदों के द्वारा प्रकाश के परिक्षेपण का एक उदाहरण है| यह सूर्य के प्रकाश का जल की गोलीय सूक्ष्म बूँदों द्वारा परिक्षेपण, अपवर्तन तथा आंतरिक परावर्तन के संयुक्त प्रभाव की परिघटना है| इंद्रधनुष देखने के लिए आवश्यक शर्तें ये हैं कि सूर्य आकाश के किसी एक भाग (मान लीजिए पश्चिमी क्षितिज) में चमक रहा हो जबकि आकाश के विपरीत भाग (मान लीजिए पूर्वी क्षितिज) में वर्षा हो रही हो| इस प्रकार कोई भी प्रेक्षक इंद्रधनुष तभी देख सकता है जब उसकी पीठ सूर्य की ओर हो|
इंद्रधनुषों का बनना समझने के लिए चित्र 9.25(a) पर विचार करते हैं| सूर्य का प्रकाश सर्वप्रथम वर्षा की बूँद में प्रवेश करते समय अपवर्तित होता है, जिसके कारण श्वेत प्रकाश की विभिन्न तरंगदैर्घ्य (वर्ण) पृथक हो जाते हैं| प्रकाश की उच्च तरंगदैर्घ्य (लाल) सबसे कम मुड़ती है जबकि निम्न तरंगदैर्घ्य (बैंगनी) सबसे अधिक मुड़ती है| इसके पश्चात ये संघटक किरणें बूँद के भीतरी पृष्ठ से टकराती हैं और यदि बूँद पृष्ठ पर अभिलंब और अपवर्तित किरण के बीच का कोण क्रांतिक कोण (इस प्रकरण में 48o) से अधिक है तो आंतरिकतः परावर्तित हो जाती है| यह परावर्तित प्रकाश, बूँद से बाहर निकलते समय चित्र में दर्शाए अनुसार पुनः अपवर्तित हो जाता है| यह पाया जाता है कि सूर्य से आने वाले प्रकाश के सापेक्ष बैंगनी प्रकाश 40o के कोण पर तथा लाल प्रकाश 42o के कोण पर निर्गत होता है| अन्य वर्णों के लिए कोणों के मान इन दोनों के मध्य होते हैं|
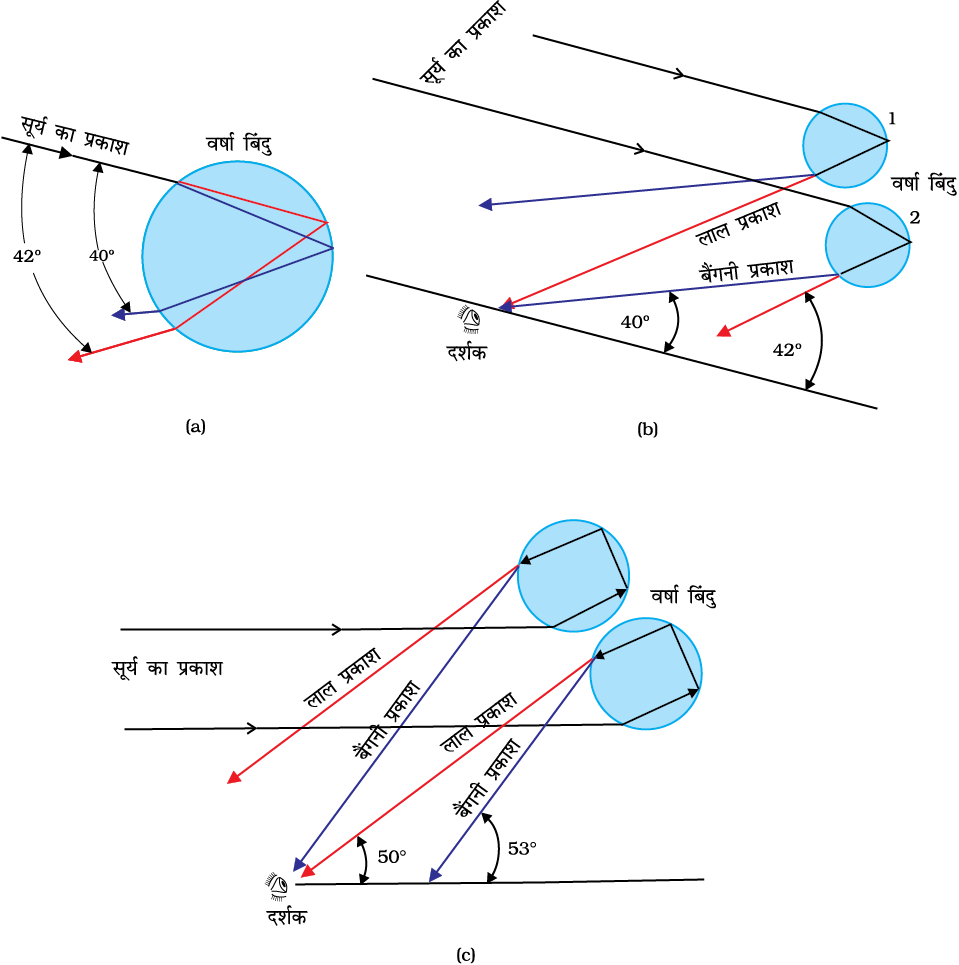
चित्र 9.25 इंद्रधनुष (a) जल की बूँद पर आपतित सूर्य की किरणों का बूँद द्वारा दो बार अपवर्तन तथा एक बार आंतरिक परावर्तन होता है, (b) बूँद के अंदर प्रकाश की किरण के आंतरिक परावर्तन तथा अपवर्तन का विवर्धित दृश्य जिसके कारण प्राथमिक इंद्रधनुष बनता है तथा (c) बूँद के अंदर किरणों के दो बार आंतरिक परावर्तन के कारण द्वितीयक इंद्रधनुष बनता है|
चित्र 9.25(b) में प्राथमिक इंद्रधनुष का बनना समझाया गया है| हम देखते हैं कि बूँद 1 से लाल प्रकाश तथा बूँद 2 से बैंगनी प्रकाश प्रेक्षक की आँखों तक पहुँचता है| बूँद 1 से आने वाला बैंगनी तथा बूँद 2 से आने वाला लाल प्रकाश प्रेक्षक की आँखों से ऊपर अथवा नीचे की ओर दिष्ट होते हैं| इस प्रकार प्रेक्षक इंद्रधनुष के शीर्ष पर लाल वर्ण और पैंदी पर बैंगनी वर्ण देखता है| इस प्रकार प्राथमिक इंद्रधनुष तीन चरणीय प्रक्रम अर्थात अपवर्तन, परावर्तन तथा पुनः अपवर्तन का परिणाम है|
जब प्रकाश किरणें किसी वर्षा की बूँद के भीतर एक बार की बजाय दो बार आंतरिकतः परावर्तित होती हैं तो द्वितीयक इंद्रधनुष बनता है [चित्र 9.25(c)]| यह चार चरणीय प्रक्रम है| द्वितीय परावर्तन के प्रक्रम में प्रकाश की तीव्रता कम हो जाती है| इसलिए द्वितीयक इंद्रधनुष प्राथमिक इंद्रधनुष की तुलना में धुँधला होता है| इसके साथ ही जैसा कि चित्र 9.25(c) से स्पष्ट है इसमें वर्णों का क्रम प्राथमिक इंद्रधनुष की तुलना में उलटा होता है|
9.7.2 प्रकाश का प्रकीर्णन
जब सूर्य का प्रकाश पृथ्वी के परिमंडल में गमन करता है तो यह वायुमंडल के कणों द्वारा प्रकीर्णित होता है| छोटी तरंगदैर्घ्य का प्रकाश बड़ी तरंगदैर्घ्यों की तुलना में कहीं अधिक प्रकीर्ण होता है| (प्रकीर्णन की मात्रा तरंगदैर्घ्य की चतुर्थ घात के व्युत्क्रमानुपाती होती है| इसे रैले प्रकीर्णन कहते हैं|) यही कारण है कि स्वच्छ आकाश में नीला वर्ण सर्वाधिक प्रमुखता दर्शाता है, क्योंकि लाल वर्ण की अपेक्षा नीले वर्ण की तरंगदैर्घ्य कम होती है तथा इसका प्रकीर्णन अधिक प्रबलता से होता है| वास्तव में बैंगनी वर्ण की तरंगदैर्घ्य और भी कम होने के कारण यह नीले वर्ण से भी अधिक प्रबलता से प्रकीर्ण होता है| लेकिन हमारी आँखें बैंगनी वर्ण की अपेक्षा नीले वर्ण के लिए अधिक सुग्राही हैं, इसलिए हमें आकाश नीला दिखाई देता है|
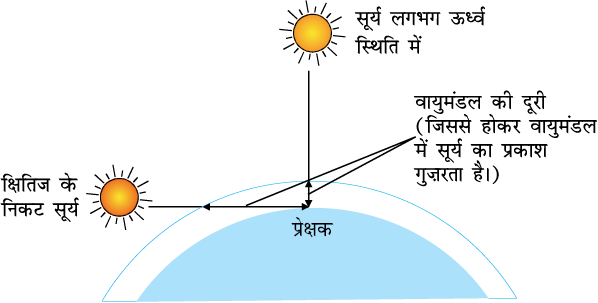
चित्र 9.26 सूर्यास्त तथा सूर्योदय के समय सूर्य का प्रकाश वायुमंडल में अधिक दूरी गमन करता है|
वायुमंडल में उपस्थित बड़े कण जैसे धूल तथा जल की सूक्ष्म बूँदं भिन्न व्यवहार दर्शाते हैं| यहाँ पर इस संदर्भ में प्रासंगिक राशि, प्रकाश की तरंगदैर्घ्य λ तथा प्रकीर्णक (मान लीजिए इनका प्रारूपी साइज़ a है) के आपेक्षिक साइज़ हैं| a << λ के लिए, रैले प्रकीर्णन होता है जो कि
(1/λ)4 के अनुक्रमानुपाती होता है| a >> λ के लिए, अर्थात बड़े साइज़ की प्रकीर्णक वस्तु के लिए (उदाहरण के लिए वर्षा की बूँदों, बड़े आकार के धूल कण अथवा हिम कण)एेसा प्रकीर्णन नहीं होता; सभी तरंगदैर्घ्य लगभग समान रूप से प्रकीर्णित होती हैं| इसीलिए बादल जिनमें a >> λ साइज़ की जल की सूक्ष्म बूँदें होती हैं, सामान्यतः श्वेत प्रतीत होते हैं|
सूर्योदय तथा सूर्यास्त के समय सूर्य की किरणों को वायुमंडल से होकर अपेक्षाकृत अधिक दूरियाँ तय करनी पड़ती हैं (चित्र 9.26)| इस प्रकाश से नीला तथा छोटी तरंगदैर्घ्य का अधिकांश प्रकाश प्रकीर्णन द्वारा पृथक हो जाता है| अतः प्रकाश का सबसे कम प्रकीर्णित भाग जो हमारी आँखों तक पहुँचता है, रक्ताभ प्रतीत होता है| यही कारण है कि क्षितिज के निकट होने पर सूर्य तथा पूर्ण चंद्रमा रक्ताभ प्रतीत होते हैं|
9.8 प्रकाशिक यंत्र
दर्पणों, लेंसों तथा प्रिज़्मों के परावर्ती तथा अपवर्ती गुणों का उपयोग करके अनेक प्रकाशिक युक्तियाँ एवं यंत्र डिज़ाइन किए गए हैं| परिदर्शी, बहुमूर्तिदर्शी, द्विनेत्री, दूरदर्शक, सूक्ष्मदर्शी कुछ एेसी प्रकाशिक युक्तियों तथा यंत्रों के उदाहरण हैं जिन्हें हम सामान्य रूप से उपयोग में लाते हैं| वास्तव में हमारे नेत्र सबसे महत्वपूर्ण प्रकाशिक युक्तियों में से एक हैं जिनसे प्रकृति ने हमें संपन्न किया है| कक्षा X में हम मानव नेत्र के बारे में पढ़ चुके हैं| अब हम सूक्ष्मदर्शी तथा दूरबीन के कार्य करने के सिद्धांत का वर्णन करेंगे|
9.8.1 सूक्ष्मदर्शी
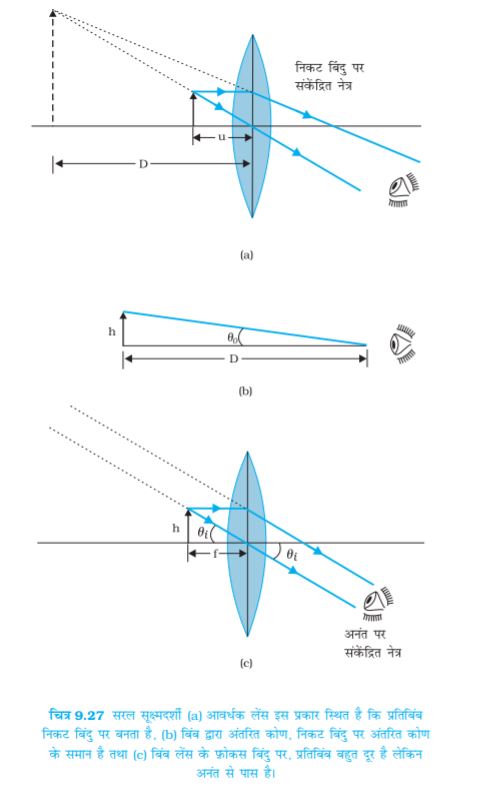
सरल आवर्धक अथवा सरल सूक्ष्मदर्शी कम फ़ोकस दूरी का एक अभिसारी लेंस होता है (चित्र 9.27)| इस प्रकार के लेंस को सूक्ष्मदर्शी के रूप में प्रयोग करने के लिए, लेंस को बिंब के निकट उससे एक फ़ोकस दूरी अथवा उससे कम दूरी पर रखा जाता है तथा लेंस के दूसरी ओर नेत्र को लेंस से सटाकर रखा जाता है| एेसा करने का लक्ष्य है कि बिंब का सीधा, आवर्धित तथा आभासी प्रतिबिंब किसी एेसी दूरी पर बने कि नेत्र उसे सरलतापूर्वक देख सकें, अर्थात प्रतिबिंब
25 cm अथवा कुछ अधिक दूरी पर बनना चाहिए| यदि बिंब f पर स्थित है तो उसका प्रतिबिंब अनंत पर बनता है| तथापि, यदि बिंब f से कम दूरी पर रखा हो, तो प्रतिबिंब आभासी तथा अनंत की तुलना में कम दूरी पर बनता है| यद्यपि देखने के लिए निकटतम आरामदेह दूरी, निकट बिंदु (दूरी D ≅ 25 cm) पर होती है, परंतु इससे नेत्रों पर कुछ तनाव पड़ता है| इसीलिए, प्रायः अनंत पर बना प्रतिबिंब शिथिल नेत्रों द्वारा देखने के लिए उचित माना जाता है| यहाँ पर दोनों स्थितियाँ दर्शायी गई हैं, पहली चित्र 9.27 (a), में तथा दूसरी चित्र 9.27 (b) तथा (c) में|
सरल सूक्ष्मदर्शी द्वारा निकट बिंदु D पर बने प्रतिबिंब के लिए रैखिक आवर्धन m का परिकलन निम्न संबंध द्वारा किया जा सकता है|
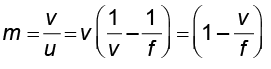
अब हमारी चिह्न परिपाटी के अनुसार v ऋणात्मक है तथा परिमाण में D के बराबर है| अतः आवर्धन,
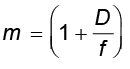 (9.39)
(9.39)
क्योंकि D लगभग 25 cm है| अतः आवर्धन 6 प्राप्त करने के लिए फ़ोकस दूरी f = 5 cm के उत्तल लेंस की आवश्यकता होती है|
ध्यान दीजिए, m = h′/h, यहाँ h बिंब का साइज़ तथा h′ प्रतिबिंब का साइज़ है| यह प्रतिबिंब द्वारा अंतरित कोण तथा बिंब द्वारा अंतरित कोण का भी अनुपात होता है, जबकि उन्हें आराम से देखने के लिए D पर रखा जाता है| (नोट कीजिए कि यह वास्तव में बिंब द्वारा नेत्र पर अंतरित कोण नहीं है, जिसे h/u द्वारा व्यक्त किया गया है|) एकल-लेंस सरल आवर्धक की उपलब्धि यह है कि वस्तु को D की तुलना में काफ़ी निकट रखकर देखना संभव हो जाता है|
अब जब प्रतिबिंब अनंत पर बनता है तो हम आवर्धन ज्ञात करेंगे| इस स्थिति में हमें कोणीय आवर्धन का परिकलन करना होगा| मान लीजिए बिंब की ऊँचाई h है| इस बिंब द्वारा नेत्र पर अंतरित अधिकतम कोण, जबकि बिंब स्पष्ट भी दिखाई देता हो (बिना किसी लेंस के), तब होता है जब हम बिंब को निकट अर्थात दूरी D पर रखते हैं| तब अंतरित कोण प्राप्त होगा
tan 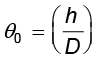 ≈ θ0 (9.40)
≈ θ0 (9.40)
अब हम प्रतिबिंब द्वारा नेत्र पर अंतरित कोण, जबकि बिंब u पर रखा है, ज्ञात करते हैं|
संबंध 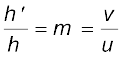 से प्रतिबिंब द्वारा नेत्र पर अंतरित कोण
से प्रतिबिंब द्वारा नेत्र पर अंतरित कोण
tan ≈θ ; बिंब द्वारा अंतरित कोण, जबकि बिंब अब u = –f पर है
≈θ ; बिंब द्वारा अंतरित कोण, जबकि बिंब अब u = –f पर है
 (9.41)
(9.41)
जैसा कि चित्र 9.27 (c) से स्पष्ट है| अतः कोणीय आवर्धन (आवर्धन क्षमता) है
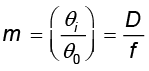 (9.42)
(9.42)
यह उस स्थिति के आवर्धन की तुलना में एक कम है, जिसमें प्रतिबिंब निकट बिंदु पर बनता है, समीकरण (9.39), परंतु प्रतिबिंब देखना अपेक्षाकृत अधिक आरामदायक होता है तथा आवर्धन में अंतर भी अपेक्षाकृत कम है| प्रकाशिक यंत्रों (सूक्ष्मदर्शी तथा दूरबीन) से संबंधित आगामी चर्चाओं में हम यह मानेंगे कि प्रतिबिंब अनंत पर बने हैं|
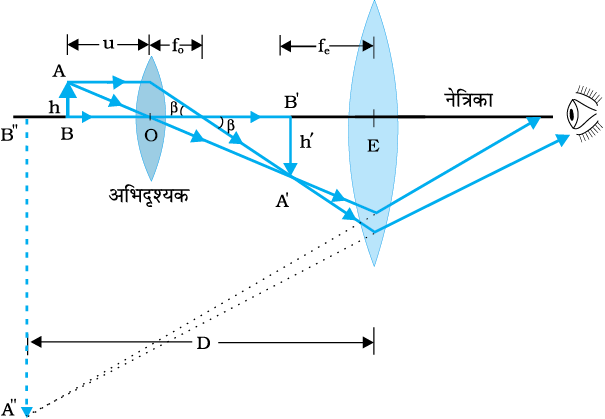
चित्र 9.28 संयुक्त सूक्ष्मदर्शी द्वारा प्रतिबिंब बनने का किरण आरेख|
वास्तविक फ़ोकस दूरियों के लेंसों के लिए किसी सरल सूक्ष्मदर्शी का अधिकतम आवर्धन (≤ 9) होता है| अधिक आवर्धन के लिए दो लेंसों का उपयोग किया जाता है, जिनमें एक लेंस दूसरे लेंस के प्रभाव को संयुक्त (बढ़ाता) करता है| इसे संयुक्त सूक्ष्मदर्शी कहते हैं| चित्र 9.28 में संयुक्त सूक्ष्मदर्शी का व्यवस्था आरेख दर्शाया गया है| बिंब के सबसे निकट के लेंस को अभिदृश्यक (objective) कहते हैं जो बिंब का वास्तविक, उलटा, आवर्धित प्रतिबिंब बनाता है| यह प्रतिबिंब दूसरे लेंस के लिए बिंब का कार्य करता है| इस दूसरे लेंस को नेत्रिका (eye-piece) कहते हैं, जो वास्तविक रूप से सरल सूक्ष्मदर्शी अथवा आवर्धक के रूप में कार्य करके अंतिम आवर्धित आभासी प्रतिबिंब बनाता है| इस प्रकार पहला उलटा प्रतिबिंब नेत्रिका के फोकस बिंदु के निकट (फ़ोकस पर या इसके अंदर) होता है, यह नेत्रिका से इतनी दूरी पर होता है जो अंतिम प्रतिबिंब को अनंत पर बनाने के लिए उपयुक्त होती है तथा उस स्थिति के भी काफ़ी निकट होती है जिस पर यदि प्रतिबिंब स्थित हो तो अंतिम निकट बिंदु पर बने| स्पष्टतः, अंतिम प्रतिबिंब मूल बिंब के सापेक्ष उलटा बनता है|
अब हम संयुक्त सूक्ष्मदर्शी के कारण आवर्धन प्राप्त करेंगे| चित्र 9.28 का किरण आरेख यह दर्शाता है कि अभिदृश्यक के कारण (रैखिक) आवर्धन, अर्थात h′/h, बराबर है
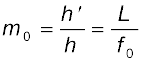 (9.43)
(9.43)
यहाँ हमने इस परिमाण का उपयोग किया है

यहाँ h′ पहले प्रतिबिंब का साइज़ है तथा बिंब का साइज़ h एवं अभिदृश्यक की फ़ोकस दूरी f0 है| पहला प्रतिबिंब नेत्रिका के फ़ोकस बिंदु के निकट बनता है| दूरी L, अर्थात, अभिदृश्यक के द्वितीय फ़ोकस बिंदु तथा नेत्रिका (फ़ोकस दूरी fe) के पहले फ़ोकस बिंदु के बीच की दूरी को संयुक्त सूक्ष्मदर्शी की ट्यूब लंबाई कहते हैं|
क्योंकि पहला उलटा प्रतिबिंब नेत्रिका के फ़ोकस बिंदु के निकट बनता है, उपरोक्त चर्चा से प्राप्त परिणाम का उपयोग हम सरल सूक्ष्मदर्शी के लिए करके इसके कारण (कोणीय) आवर्धन me प्राप्त करते हैं [समीकरण 9.39], जबकि अंतिम प्रतिबिंब किसी निकट बिंदु पर बनता है| यह है
 [9.44(a)]
[9.44(a)]
जब प्रतिबिंब अनंत पर बनता है तो नेत्रिका के कारण कोणीय आवर्धन [समीकरण (9.42)] है
me = (D/fe) [9.44(b)]
अतः कुल आवर्धन [समीकरण (9.33) के अनुसार], जबकि प्रतिबिंब अनंत पर बनता है, है
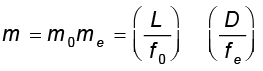 (9.45)
(9.45)
स्पष्ट है कि किसी छोटी वस्तु का बड़ा आवर्धन प्राप्त करने के लिए (इसीलिए सूक्ष्मदर्शी नाम रखा गया है) अभिदृश्यक तथा नेत्रिका की फ़ोकस दूरी कम होनी चाहिए| व्यवहार में,1 cm से कम फ़ोकस दूरी का लेंस बनाना अत्यंत कठिन कार्य है| इसी के साथ L को बड़ा करने के लिए बड़े लेेंसों की आवश्यकता होती है|
उदाहरण के लिए, किसी fo = 1.0 cm के अभिदृश्यक fe = 2.0 cm की नेत्रिका तथा ट्यूब लंबाई (L) = 20 cm के लिए संयुक्त सूक्ष्मदर्शी का आवर्धन
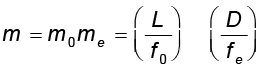
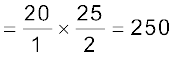
अन्य विभिन्न कारक जैसे वस्तु की प्रदीप्ति भी प्रतिबिंब की दृश्यता एवं गुणता में महत्वपूर्ण योगदान देते हैं| आधुनिक सूक्ष्मदर्शियों में, अभिदृश्यक तथा नेत्रिका बहुअवयवी लेंसों द्वारा बनाए जाते हैं, जिनके कारण लेंसों के प्रकाशिक विपथनों (दोष) को कम करके प्रतिबिंबों की गुणता में सुधार किया जाता है|
9.8.2 दूरदर्शक
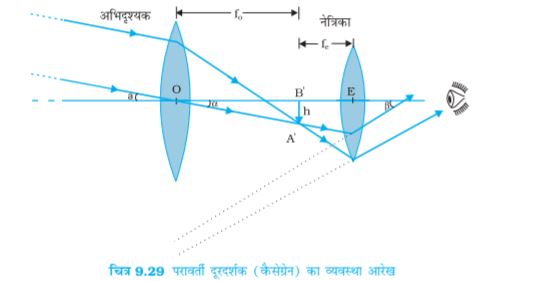
दूरदर्शक अथवा दूरबीन (चित्र 9.29) का उपयोग दूर की वस्तुओं को कोणीय आवर्धन प्रदान करने के लिए किया जाता है| इसमें भी एक अभिदृश्यक तथा एक नेत्रिका होती है| परंतु यहाँ पर, नेत्रिका की अपेक्षा अभिदृश्यक की फ़ोकस दूरी अधिक तथा इसका द्वारक भी काफ़ी अधिक होता है| किसी दूरस्थ बिंब से चलकर प्रकाश अभिदृश्यक में प्रवेश करता है तथा ट्यूब के अंदर इसके द्वितीय फ़ोकस पर वास्तविक प्रतिबिंब बनता है| नेत्रिका इस प्रतिबिंब को आवर्धित करके अंतिम उलटा प्रतिबिंब बनाती है| आवर्धन क्षमता m, प्रतिबिंब द्वारा नेत्र पर अंतरित कोण β तथा बिंब द्वारा नेत्र पर अथवा लेंस पर अंतरित कोण α के अनुपात द्वारा परिभाषित किया जाता है| अतः
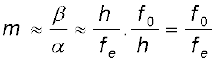 (9.46)
(9.46)
इस स्थिति में, दूरदर्शक की ट्यूब की लंबाई है fo + fe
पार्थिव दूरदर्शकों में, इन लेंसों के अतिरिक्त, प्रतिलोमी लेंसों का एक युगल होता है जो अंतिम प्रतिबिंब को सीधा बना देता है| अपवर्ती दूरदर्शक का उपयोग पार्थिव एवं खगोलीय दोनों प्रकार के प्रेक्षणों के लिए किया जा सकता है| उदाहरण के लिए, किसी एेसे दूरदर्शक पर विचार कीजिए जिसके अभिदृश्यक की फ़ोकस दूरी 100 cm तथा नेत्रिका की फ़ोकस दूरी 1 cm है| इस दूरबीन की आवर्धन क्षमता m = 100/1 = 100
अब किन्हीं दो तारों के युगल पर विचार कीजिए जिनका वास्तविक पृथकन 1′ (1 मिनट का चाप) है| ये तारे उपरोक्त दूरदर्शक से देखने पर इस प्रकार प्रतीत होते हैं जैसे कि इनके बीच के पृथकन-कोण 100 × 1′ = 100′ =1.67º है|
किसी खगोलीय दूरदर्शक के बारे में ध्यान देने योग्य मुख्य बातें उसकी प्रकाश संग्रहण क्षमता तथा इसकी विभेदन क्षमता अथवा विभेदन है| प्रकाश संग्रहण क्षमता स्पष्ट रूप से दूरदर्शक के अभिदृश्यक के क्षेत्रफल पर निर्भर करती है| यदि अभिदृश्यक का व्यास बड़ा है तो धुँधले पिंडाें का भी प्रेक्षण किया जा सकता है| विभेदन क्षमता अथवा एक ही दिशा में दो अत्यधिक निकट की वस्तुओं को सुस्पष्टतः भिन्न प्रेक्षित करने की योग्यता भी अभिदृश्यक के व्यास पर निर्भर करती है| अतः प्रकाशिक दूरदर्शक में वांछित उद्देश्य यह होता है| कि अभिदृश्यक का व्यास अधिकतम हो| आजकल उपयोग होने वाले अभिदृश्यक लेंस का अधिकतम व्यास 40 इंच (~1.02 m) है| यह दूरदर्शक यर्केज वेधशाला, विस्कॉनसिन, संयुक्त राज्य अमेरिका मेें है| इतने बड़े लेंस अत्यधिक भारी होते हैं, अतः इन्हें बनाना तथा किनारों के सहारे टिकाकर रखना कठिन कार्य है| इसके अतिरिक्त इतने बड़े साइज़ के लेंसों को इस प्रकार बनाना कि प्रतिबिंबों में वर्ण विपथन तथा अन्य विरूपण न आएँ, बहुत कठिन तथा महँगा कार्य है|
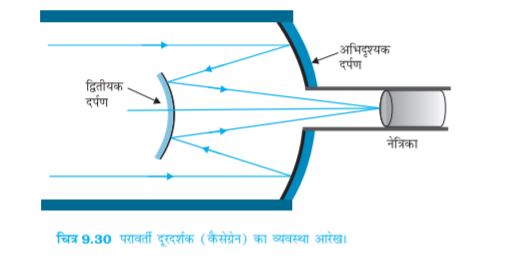
यही कारण है कि आधुनिक दूरदर्शकों में अभिदृश्यक के रूप में लेंस के स्थान पर अवतल दर्पण का उपयोग किया जाता है| एेसे दूरदर्शकों को जिनमें अभिदृश्यक दर्पण हेाता है, परावर्ती दूरदर्शक (दूरबीन) कहते हैं| दर्पण में कोई वर्ण विपथन नहीं होता| यांत्रिक सहारा देने की समस्या भी काफ़ी कम होती है क्योंकि लेंस की तुलना में, तुल्य प्रकाशिक गुणता का दर्पण अपेक्षाकृत कम भारी होता है तथा दर्पण को केवल रिम पर ही सहारा देने की बजाय उसके समस्त पीछे के पृष्ठ को सहारा प्रदान किया जा सकता है| परावर्ती दूरबीन की एक सुस्पष्ट समस्या यह होती है कि अभिदृश्यक दर्पण दूरदर्शक की नली के भीतर प्रकाश को फ़ोकसित करता है| अतः नेत्रिका तथा प्रेक्षक को उसी स्थान पर होना चाहिए जिससे प्रकाश के मार्ग में अवरोध के कारण कुछ प्रकाश कम हो जाता है (यह अवरोध प्रेक्षक के बैठने के लिए बनाए गए पिंजरेनुमा कमरे के साइज़ पर निर्भर करता है)| एेसा ही प्रयोग अति विशाल 200 इंच (~5.08 m) व्यास के माउंट पेलोमर दूरदर्शक, कैलिफ़ोर्निया में किया गया है| प्रेक्षक एक छोटे पिंजरे में दर्पण के फ़ोकस बिंदु के निकट बैठता है| इस समस्या का एक अन्य समाधान यह है कि फोकसित होने वाले प्रकाश को किसी अन्य दर्पण द्वारा विक्षेपित कर दिया जाए| एेसी ही एक व्यवस्था चित्र 9.30 में दर्शायी गई है, जिसमें आपतित प्रकाश को फ़ोकसित करने के लिए किसी उत्तल द्वितीयक दर्पण का उपयोग किया जाता है जो अब अभिदृश्यक (प्राथमिक दर्पण) के छिद्र से गुज़रता है| इस दूरदर्शक को इसके आविष्कारक के नाम पर कैसेग्रेन दूरदर्शक (Cassegrain telescope) कहते हैं| इसका एक लाभ यह है कि छोटे दूरदर्शक में बड़ी फ़ोकस दूरी होती है| भारतवर्ष में सबसे बड़ा दूरदर्शक कवलूर, तमिलनाडु में है| यह 2.34 m व्यास की कैसेग्रेन परावर्ती दूरदर्शक है| इसे घर्षित किया गया, फिर पॉलिश की गई और व्यवस्थित किया गया तथा अब इसे भारतीय खगोल भौतिकी संस्थान, बंगलुरू द्वारा प्रयोग किया जा रहा है| संसार का सबसे बड़ा परावर्ती दूरदर्शक हवाई, संयुक्त राज्य अमेरिका में कैक दूरदर्शकों का युगल है जिसके परावर्तक का व्यास 10 मीटर है|
सारांश
1. परावर्तन समीकरण ∠i = ∠r′ द्वारा तथा अपवर्तन स्नेल के नियम sini/sinr = n द्वारा अभिनियंत्रित होता है, जहाँ आपतित किरण, परावर्तित किरण, अपवर्तित किरण तथा अभिलंब एक ही समतल में होते हैं| यहाँ पर कोण i, r ′ तथा r, क्रमशः आपतन कोण, परावर्तन कोण तथा अपवर्तन कोण हैं|
2. सघन माध्यम से विरल माध्यम में आपतित किरण के लिए क्रांतिक आपतन कोण ic वह कोण है जिसके लिए अपवर्तन कोण 90°है| i > ic होने पर पूर्ण आंतरिक परावर्तन होता है| हीरे में बहुगुणित आंतरिक परावर्तन (ic ≅ 24.4°), पूर्ण परावर्तक प्रिज़्म तथा मरीचिका, पूर्ण आंतरिक परावर्तन के कुछ उदाहरण हैं| प्रकाशिक तंतु, काँच के तंतुओं के बने होते हैं जिन पर अपेक्षाकृत कम अपवर्तनांक के पदार्थ की पतली परत का लेपन होता है| प्रकाशिक तंतु के किसी एक सिरे पर आपतित प्रकाश, बहुगुणित आंतरिक परावर्तन द्वारा दूसरे सिरे से निकलता है, प्रकाशिक तंतु के मुड़ा होने पर भी एेसा होता है|
3. कार्तीय चिह्न परिपाटी– आपतित प्रकाश की दिशा में मापी गई दूरियाँ धनात्मक तथा इसके विपरीत दिशा में मापी गई दूरियाँ ऋणात्मक ली जाती हैं| सभी दूरियाँ मुख्य अक्ष पर दर्पण के ध्रुव/लेंस के प्रकाशिक केंद्र से मापी जाती हैं| x-अक्ष के उपरिमुखी तथा दर्पण/लेंस के मुख्य अक्ष के अभिलंबवत मापी गई ऊँचाइयाँ धनात्मक ली जाती हैं| अधोमुखी दिशा में मापी गई ऊँचाइयाँ ऋणात्मक ली जाती हैं|
4. दर्पण समीकरण
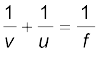
यहाँ u तथा v क्रमशः बिंब दूरी तथा प्रतिबिंब दूरी हैं तथा f दर्पण की फ़ोकस दूरी है| f (सन्निकटतः) वक्रता त्रिज्या R की आधी होती है| अवतल दर्पण के लिए f ऋणात्मक तथा उत्तल दर्पण के लिए f धनात्मक होता है|
5. प्रिज़्म कोण A, अपवर्तनांक n2 के किसी प्रिज़्म के लिए जो n1 अपवर्तनांक के किसी माध्यम में रखा है|
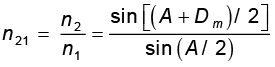
यहाँ Dm न्यूनतम विचलन कोण है|
6. किसी गोलीय अंतरापृष्ठ से अपवर्तन [माध्यम 1 (अपवर्तनांक n1) से माध्यम 2 (अपवर्तनांक n2) की ओर]
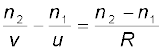
पतले लेंस के लिए सूत्र
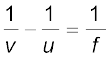
लेंस-मेकर सूत्र
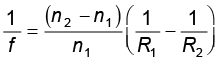
R1 तथा R2 लेंस के पृष्ठों की वक्रता त्रिज्याएँ हैं| अभिसारी लेंस के लिए f धनात्मक है; अपसारी लेंस के लिए f ऋणात्मक है| लेंस की क्षमता P = 1/f |
लेंस की क्षमता का SI मात्रक डाइअॉप्टर (D) है; 1 D = 1 m–1|
यदि f1, f2, f3,.. फ़ोकस दूरी के कई पतले लेंस संपर्क में रखे हों तो इस संयोजन की प्रभावी फ़ोकस दूरी होगी
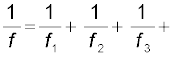 …
…
अनेक लेंसों के संयोजन की कुल क्षमता
P = P1 + P2 + P3 + …
7. प्रकाश का परिक्षेपण, प्रकाश का अपने संघटक वर्णों में विपाटन (विघटन) होता है|
8. किसी सरल सूक्ष्मदर्शी की आवर्धन क्षमता के परिमाण m को m = 1 + (D/f) द्वारा व्यक्त किया जाता है, यहाँ D = 25 cm, स्पष्ट दर्शन की अल्पतम दूरी है तथा f उत्तल लेंस की फोकस दूरी है| यदि प्रतिबिंब अनंत पर बने तब m = D/f होगा| किसी संयुक्त सूक्ष्मदर्शी के लिए आवर्धन क्षमता m को m = me × m0 के द्वारा व्यक्त किया जाता है, यहाँ
me = 1 + (D/fe) नेत्रिका का आवर्धन तथा m0 अभिदृश्यक द्वारा उत्पन्न आवर्धन है| सन्निकटतः
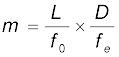
यहाँ fo तथा fe क्रमशः अभिदृश्यक तथा नेत्रिका की फ़ोकस दूरियाँ हैं तथा L इन दोनों के फ़ोकस बिंदुओं के बीच की दूरी है|
9. किसी दूरबीन की आवर्धन क्षमता, प्रतिबिंब द्वारा नेत्र पर अंतरित कोण β तथा बिंब द्वारा नेत्र पर अंतरित कोण α का अनुपात होती है|
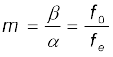 ,
,
यहाँ f0 तथा fe क्रमशः अभिदृश्यक तथा नेत्रिका की फ़ोकस दूरियाँ हैं|
विचारणीय विषय
1. आपतन बिंदु पर परावर्तन तथा अपवर्तन के नियम सभी पृष्ठों तथा माध्यमों के युगलों के लिए मान्य हैं|
2. किसी उत्तल लेंस से f तथा 2 f के बीच रखे किसी बिंब के वास्तविक प्रतिबिंब को प्रतिबिंब-स्थिति पर रखे पर्दे पर देखा जा सकता है| यदि पर्दे को हटा दें तो क्या फिर भी प्रतिबिंब वहाँ रहता है? यह प्रश्न बहुतों को दुविधा में डालता है, क्योंकि हमें स्वयं को भी यह समझा पाना कठिन होता है कि कोई प्रतिबिंब बिना किसी पर्दे के वायु में निलंबित कैसे रह सकता है| परंतु प्रतिबिंब तो वहाँ रहता ही है| बिंब के किसी बिंदु से निर्गत प्रकाश किरणें दिक्स्थान में किसी प्रतिबिंब बिंदु पर अभिसरित होकर अपसरित हो जाती हैं| परदा केवल इन किरणों को विसरित करता है जिनमें से कुछ किरणें हमारे नेत्रों तक पहुँचती हैं और हम प्रतिबिंब देख पाते हैं| किसी लेज़र प्रदर्शन के समय बने प्रतिबिंबों द्वारा इसे देखा जा सकता है|
3. प्रतिबिंब बनने के लिए नियमित परावर्तन/अपवर्तन की आवश्यकता होती है| सिद्धांत रूप में, किसी बिंदु से निर्गत सभी किरणें एक ही प्रतिबिंब बिंदु पर पहुँचनी चाहिए| यही कारण है कि आप किसी अनियमित परावर्ती पृष्ठ, जैसे किसी पुस्तक के पृष्ठ में अपना प्रतिबिंब नहीं देखते|
4. मोटे लेंस परिक्षेपण के कारण रंगीन प्रतिबिंब बनाते हैं| हमारे चारों ओर की वस्तुओं के रंगों में विविधता उन पर आपतित प्रकाश के रंगों के संघटकों के कारण होती है| किसी वस्तु को एकवर्णी प्रकाश में देखने पर तथा श्वेत प्रकाश में देखने पर उस वस्तु के विषय में बिलकुल ही अलग बोध होता है|
5. किसी सरल सूक्ष्मदर्शी के लिए बिंब का कोणीय साइज़, प्रतिबिंब के कोणीय साइज़ के बराबर होता है| फिर भी वह आवर्धन प्रदान करता है क्योंकि आप सूक्ष्मदर्शी का उपयोग करते समय किसी छोटी वस्तु को अपने नेत्रों के बहुत निकट (25 cm से भी कम दूरी पर) रख सकते हैं, जिसके फलस्वरूप वह नेत्र पर बड़ा कोण अंतरित करता है| प्रतिबिंब, जिसे हम देख सकते हैं, 25 cm दूरी पर है| बिना सूक्ष्मदर्शी के आपको उस छोटी वस्तु को स्पष्ट देख पाने के लिए 25 cm दूरी पर रखना होगा और तब वह आपके नेत्र पर बहुत छोटा कोण अंतरित करेगा|
अभ्यास
9.1 2.5 cm साइज़ की कोई छोटी मोमबत्ती 36 cm वक्रता त्रिज्या के किसी अवतल दर्पण से 27 cm दूरी पर रखी है| दर्पण से किसी परदे को कितनी दूरी पर रखा जाए कि उसका सुस्पष्ट प्रतिबिंब परदे पर बने| प्रतिबिंब की प्रकृति और साइज़ का वर्णन कीजिए| यदि मोमबत्ती को दर्पण की ओर ले जाएँ, तो परदे को किस ओर हटाना पड़ेगा?
9.2 4.5 cm साइज़ की कोई सुई 15 cm फोकस दूरी के किसी उत्तल दर्पण से 12 cm दूर रखी है| प्रतिबिंब की स्थिति तथा आवर्धन लिखिए| क्या होता है जब सुई को दर्पण से दूर ले जाते हैं? वर्णन कीजिए|
9.3 कोई टैंक 12.5 cm ऊँचाई तक जल से भरा है| किसी सूक्ष्मदर्शी द्वारा बीकर की तली पर पड़ी किसी सुई की आभासी गहराई 9.4 cm मापी जाती है| जल का अपवर्तनांक क्या है? बीकर में उसी ऊँचाई तक जल के स्थान पर किसी 1.63 अपवर्तनांक के अन्य द्रव से प्रतिस्थापन करने पर सुई को पुनः फ़ोकसित करने के लिए सूक्ष्मदर्शी को कितना ऊपर/नीचे ले जाना होगा?

9.4 चित्र 9.31 (a) तथा (b) में किसी आपतित किरण का अपवर्तन दर्शाया गया है जो वायु में क्रमशः काँच-वायु तथा जल-वाय अंतरापृष्ठ के अभिलंब से 60o का कोण बनाती है| उस आपतित किरण का अपवर्तन कोण ज्ञात कीजिए, जो जल में जल-काँच अंतरापृष्ठ के अभिलंब से 45o का कोण बनाती है [चित्र 9.31 (c)]|
9.5 जल से भरे 80 cm गहराई के किसी टैंक की तली पर कोई छोटा बल्ब रखा गया है| जल के पृष्ठ का वह क्षेत्र ज्ञात कीजिए जिससे बल्ब का प्रकाश निर्गत हो सकता है| जल का अपवर्तनांक 1.33 है| (बल्ब को बिंदु प्रकाश स्रोत मानिए|)
9.6 कोई प्रिज़्म अज्ञात अपवर्तनांक के काँच का बना है| कोई समांतर प्रकाश-पुंज इस प्रिज़्म के किसी फलक पर आपतित होता है| प्रिज़्म का न्यूनतम विचलन कोण 40o मापा गया| प्रिज़्म के पदार्थ का अपवर्तनांक क्या है? प्रिज़्म का अपवर्तन कोण 60o है| यदि प्रिज़्म को जल (अपवर्तनांक 1.33) में रख दिया जाए तो प्रकाश के समांतर पुंज के लिए नए न्यूनतम विचलन कोण का परिकलन कीजिए|
9.7 अपवर्तनांक 1.55 के काँच से दोनों फलकों की समान वक्रता त्रिज्या के उभयोत्तल लेंस निर्मित करने हैं| यदि 20 cm फ़ोकस दूरी के लेंस निर्मित करने हैं तो अपेक्षित वक्रता त्रिज्या क्या होगी?
9.8 कोई प्रकाश-पुंज किसी बिंदु P पर अभिसरित होता है| कोई लेंस इस अभिसारी पुंज के पथ में बिंदु P से 12 cm दूर रखा जाता है| यदि यह (a) 20 cm फ़ोकस दूरी का उत्तल लेंस है, (b) 16 cm फ़ोकस दूरी का अवतल लेंस है, तो प्रकाश-पुंज किस बिंदु पर अभिसरित होगा?
9.9 3.0 cm ऊँची कोई बिंब 21 cm फ़ोकस दूरी के अवतल लेंस के सामने 14 cm दूरी पर रखी है| लेंस द्वारा निर्मित प्रतिबिंब का वर्णन कीजिए| क्या होता है जब बिंब लेंस से दूर हटती
जाती है?
9.10 किसी 30 cm फ़ोकस दूरी के उत्तल लेंस के संपर्क में रखे 20 cm फ़ोकस दूरी के अवतल लेंस के संयोजन से बने संयुक्त लेंस (निकाय) की फ़ोकस दूरी क्या है? यह तंत्र अभिसारी लेंस है अथवा अपसारी? लेंसों की मोटाई की उपेक्षा कीजिए|
9.11 किसी संयुक्त सूक्ष्मदर्शी में 2.0 cm फ़ोकस दूरी का अभिदृश्यक लेंस तथा 6.25 cm फ़ोकस दूरी का नेत्रिका लेंस एक-दूसरे से 15 cm दूरी पर लगे हैं| किसी बिंब को अभिदृश्यक से कितनी दूरी पर रखा जाए कि अंतिम प्रतिबिंब (a) स्पष्ट दर्शन की अल्पतम दूरी (25 cm) तथा (b) अनंत पर बने? दोनों स्थितियों में सूक्ष्मदर्शी की आवर्धन क्षमता ज्ञात कीजिए|
9.12 25 cm के सामान्य निकट बिंदु का कोई व्यक्ति एेसे संयुक्त सूक्ष्मदर्शी जिसका अभिदृश्यक
8.0 mm फ़ोकस दूरी तथा नेत्रिका 2.5 cm फ़ोकस दूरी की है, का उपयोग करके अभिदृश्यक से 9.0 mm दूरी पर रखे बिंब को सुस्पष्ट फ़ोकसित कर लेता है| दोनों लेंसों के बीच पृथकन दूरी क्या है? सूक्ष्मदर्शी की आवर्धन क्षमता क्या है?
9.13 किसी छोटी दूरबीन के अभिदृश्यक की फ़ोकस दूरी 144 cm तथा नेत्रिका की फ़ोकस दूरी 6.0 cm है| दूरबीन की आवर्धन क्षमता कितनी है? अभिदृश्यक तथा नेत्रिका के बीच पृथकन दूरी क्या है?
9.14 (a) किसी वेधशाला की विशाल दूरबीन के अभिदृश्यक की फ़ोकस दूरी 15 m है| यदि 1.0 cm फ़ोकस दूरी की नेत्रिका प्रयुक्त की गयी है, तो दूरबीन का कोणीय आवर्धन क्या है?
(b) यदि इस दूरबीन का उपयोग चंद्रमा का अवलोकन करने में किया जाए तो अभिदृश्यक लेंस द्वारा निर्मित चंद्रमा के प्रतिबिंब का व्यास क्या है? चंद्रमा का व्यास 3.48 × 106 m तथा चंद्रमा की कक्षा की त्रिज्या 3.8 × 108 m है|
9.15 दर्पण-सूत्र का उपयोग यह व्युत्पन्न करने के लिए कीजिए कि
(a) किसी अवतल दर्पण के f तथा 2f के बीच रखे बिंब का वास्तविक प्रतिबिंब 2f से दूर बनता है|
(b) उत्तल दर्पण द्वारा सदैव आभासी प्रतिबिंब बनता है जो बिंब की स्थिति पर निर्भर नहीं करता|
(c) उत्तल दर्पण द्वारा सदैव आकार में छोटा प्रतिबिंब, दर्पण के ध्रुव व फ़ोकस के बीच बनता है|
(d) अवतल दर्पण के ध्रुव तथा फ़ोकस के बीच रखे बिंब का आभासी तथा बड़ा प्रतिबिंब
बनता है|
(नोट ः यह अभ्यास आपकी बीजगणितीय विधि द्वारा उन प्रतिबिंबों के गुण व्युत्पन्न करने में सहायता करेगा जिन्हें हम किरण आरेखों द्वारा प्राप्त करते हैं|)
9.16 किसी मेज के ऊपरी पृष्ठ पर जड़ी एक छोटी पिन को 50 cm ऊँचाई से देखा जाता है|
15 cm मोटे आयताकार काँच के गुटके को मेज़ के पृष्ठ के समांतर पिन व नेत्र के बीच रखकर उसी बिंदु से देखने पर पिन नेत्र से कितनी दूर दिखाई देगी? काँच का अपवर्तनांक 1.5 है| क्या उत्तर गुटके की अवस्थिति पर निर्भर करता है?
9.17 निम्नलिखित प्रश्नों के उत्तर लिखिए ः
(a) चित्र 9.32 में अपवर्तनांक 1.68 के तंतु काँच से बनी किसी ‘प्रकाश नलिका’ (लाइट पाइप) का अनुप्रस्थ परिच्छेद दर्शाया गया है| नलिका का बाह्य आवरण 1.44 अपवर्तनांक के पदार्थ का बना है| नलिका के अक्ष से आपतित किरणों के कोणों का परिसर, जिनके लिए चित्र में दर्शाए अनुसार नलिका के भीतर पूर्ण परावर्तन होते हैं, ज्ञात कीजिए|
(b) यदि पाइप पर बाह्य आवरण न हो तो क्या उत्तर होगा?
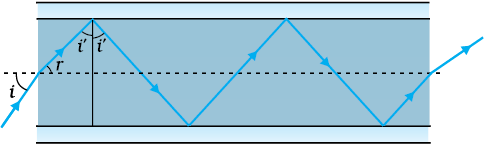
चित्र 9.32
9.18 निम्नलिखित प्रश्नों के उत्तर लिखिए ः
(a) आपने सीखा है कि समतल तथा उत्तल दर्पण सदैव आभासी प्रतिबिंब बनाते हैं| क्या ये दर्पण किन्हीं परिस्थितियों में वास्तविक प्रतिबिंब बना सकते हैं? स्पष्ट कीजिए|
(b) हम सदैव कहते हैं कि आभासी प्रतिबिंब को परदे पर केंद्रित नहीं किया जा सकता| यद्यपि जब हम किसी आभासी प्रतिबिंब को देखते हैं तो हम इसे स्वाभाविक रूप में अपनी आँख की स्क्रीन (अर्थात रेटिना) पर लाते हैं| क्या इसमें कोई विरोधाभास है?
(c) किसी झील के तट पर खड़ा मछुआरा झील के भीतर किसी गोताखोर द्वारा तिरछा देखने पर अपनी वास्तविक लंबाई की तुलना में कैसा प्रतीत होगा–छोटा अथवा लंबा?
(d) क्या तिरछा देखने पर किसी जल के टैंक की आभासी गहराई परिवर्तित हो जाती है? यदि हाँ, तो आभासी गहराई घटती है अथवा बढ़ जाती है?
(e) सामान्य काँच की तुलना में हीरे का अपवर्तनांक काफ़ी अधिक होता है? क्या हीरे को तराशने वालों के लिए इस तथ्य का कोई उपयोग होता है?
9.19 किसी कमरे की एक दीवार पर लगे विद्युत बल्ब का किसी बड़े आकार के उत्तल लेंस द्वारा
3 m दूरी पर स्थित सामने की दीवार पर प्रतिबिंब प्राप्त करना है| इसके लिए उत्तल लेंस की अधिकतम फ़ोकस दूरी क्या होनी चाहिए?
9.20 किसी परदे को बिंब से 90 cm दूर रखा गया है| परदे पर किसी उत्तल लेंस द्वारा उसे एक-दूसरे से 20 cm दूर स्थितियों पर रखकर, दो प्रतिबिंब बनाए जाते हैं| लेंस की फ़ोकस दूरी ज्ञात कीजिए|
9.21 (a) प्रश्न 9.10 के दो लेंसों के संयोजन की प्रभावी फ़ोकस दूरी उस स्थिति में ज्ञात कीजिए जब उनके मुख्य अक्ष संपाती हैं, तथा ये एक-दूसरे से 8 cm दूरी पर रखे हैं| क्या उत्तर आपतित समांतर प्रकाश पुंज की दिशा पर निर्भर करेगा? क्या इस तंत्र के लिए प्रभावी फ़ोकस दूरी किसी भी रूप में उपयोगी है?
(b) उपरोक्त व्यवस्था (a) में 1.5 cm ऊँचा कोई बिंब उत्तल लेंस की ओर रखा है| बिंब की उत्तल लेंस से दूरी 40 cm है| दो लेंसों के तंत्र द्वारा उत्पन्न आवर्धन तथा प्रतिबिंब का आकार ज्ञात कीजिए|
9.22 60° अपवर्तन कोण के प्रिज़्म के फलक पर किसी प्रकाश किरण को किस कोण पर आपतित कराया जाए कि इसका दूसरे फलक से केवल पूर्ण आंतरिक परावर्तन ही हो? प्रिज़्म के पदार्थ का अपवर्तनांक 1.524 है|
9.23 कोई कार्ड शीट जिसे 1 mm2 साइज़ के वर्गों में विभाजित किया गया है, को 9 cm दूरी पर रखकर किसी आवर्धक लेंस (9 cm फ़ोकस दूरी का अभिसारी लेंस) द्वारा उसे नेत्र के निकट रखकर देखा जाता है|
(a) लेंस द्वारा उत्पन्न आवर्धन (प्रतिबिंब-साइज़/वस्तु-साइज़) क्या है? आभासी प्रतिबिंब में प्रत्येक वर्ग का क्षेत्रफल क्या है?
(b) लेंस का कोणीय आवर्धन (आवर्धन क्षमता) क्या है?
(c) क्या (a) में आवर्धन क्षमता (b) में आवर्धन के बराबर है? स्पष्ट कीजिए|
9.24 (a) अभ्यास 9.23 में लेंस को चित्र से कितनी दूरी पर रखा जाए ताकि वर्गों को अधिकतम संभव आवर्धन क्षमता के साथ सुस्पष्ट देखा जा सके?
(b) इस उदाहरण में आवर्धन (प्रतिबिंब-साइज़/वस्तु-साइज़) क्या है?
(c) क्या इस प्रक्रम में आवर्धन, आवर्धन क्षमता के बराबर है? स्पष्ट कीजिए|
9.25 अभ्यास 9.24 में वस्तु तथा आवर्धक लेंस के बीच कितनी दूरी होनी चाहिए ताकि आभासी प्रतिबिंब में प्रत्येक वर्ग 6.25 mm2 क्षेत्रफल का प्रतीत हो? क्या आप आवर्धक लेंस को नेत्र के अत्यधिक निकट रखकर इन वर्गों को सुस्पष्ट देख सकेंगे?
[नोट – अभ्यास 9.23 से 9.25 आपको निरपेक्ष साइज़ में आवर्धन तथा किसी यंत्र की आवर्धन क्षमता (कोणीय आवर्धन) के बीच अंतर को स्पष्टतः समझने में सहायता करेंगे|]
9.26 निम्नलिखित प्रश्नों के उत्तर दीजिए–
(a) किसी वस्तु द्वारा नेत्र पर अंतरित कोण आवर्धक लेंस द्वारा उत्पन्न आभासी प्रतिबिंब द्वारा नेत्र पर अंतरित कोण के बराबर होता है| तब फिर किन अर्थों में कोई आवर्धक लेंस कोणीय आवर्धन प्रदान करता है?
(b) किसी आवर्धक लेंस से देखते समय प्रेक्षक अपने नेत्र को लेंस से अत्यधिक सटाकर रखता है| यदि प्रेक्षक अपने नेत्र को पीछे ले जाए तो क्या कोणीय आवर्धन परिवर्तित हो जाएगा?
(c) किसी सरल सूक्ष्मदर्शी की आवर्धन क्षमता उसकी फ़ोकस दूरी के व्युत्क्रमानुपाती होती है| तब हमें अधिकाधिक आवर्धन क्षमता प्राप्त करने के लिए कम से कम फ़ोकस दूरी के उत्तल लेंस का उपयोग करने से कौन रोकता है?
(d) किसी संयुक्त सूक्ष्मदर्शी के अभिदृश्यक लेंस तथा नेत्रिका लेंस दोनों ही की फ़ोकस दूरी कम क्यों होनी चाहिए?
(e) संयुक्त सूक्ष्मदर्शी द्वारा देखते समय सर्वोत्तम दर्शन के लिए हमारे नेत्र, नेत्रिका पर स्थित न होकर उससे कुछ दूरी पर होने चाहिए| क्यों? नेत्र तथा नेत्रिका के बीच की यह अल्प दूरी कितनी होनी चाहिए?
9.27 1.25 cm फोकस दूरी का अभिदृश्यक तथा 5 cm फ़ोकस दूरी की नेत्रिका का उपयोग करके वांछित कोणीय आवर्धन (आवर्धन क्षमता) 30 X होता है| आप संयुक्त सूक्ष्मदर्शी का समायोजन कैसे करेंगे?
9.28 किसी दूरबीन के अभिदृश्यक की फोकस दूरी 140 cm तथा नेत्रिका की फोकस दूरी 5.0 cm है| दूर की वस्तुओं को देखने के लिए दूरबीन की आवर्धन क्षमता क्या होगी जब–
(a) दूरबीन का समायोजन सामान्य है (अर्थात अंतिम प्रतिबिंब अनंत पर बनता है)|
(b) अंतिम प्रतिबिंब स्पष्ट दर्शन की अल्पतम दूरी (25 cm) पर बनता है|
9.29 (a) अभ्यास 9.28(a) में वर्णित दूरबीन के लिए अभिदृश्यक लेंस तथा नेत्रिका के बीच पृथकन दूरी क्या है?
(b) यदि इस दूरबीन का उपयोग 3 km दूर स्थित 100 m ऊँची मीनार को देखने के लिए किया जाता है तो अभिदृश्यक द्वारा बने मीनार के प्रतिबिंब की ऊँचाई क्या है?
(c) यदि अंतिम प्रतिबिंब 25 cm दूर बनता है तो अंतिम प्रतिबिंब में मीनार की ऊँचाई क्या है?
9.30 किसी कैसेग्रेन दूरबीन में चित्र 9.30 में दर्शाए अनुसार दो दर्पणों का प्रयोग किया गया है| इस दूरबीन में दोनों दर्पण एक-दूसरे से 20 mm दूर रखे गए हैं| यदि बड़े दर्पण की वक्रता त्रिज्या 220 mm हो तथा छोटे दर्पण की वक्रता त्रिज्या 140 mm हो तो अनंत पर रखे किसी बिंब का अंतिम प्रतिबिंब कहाँ बनेगा?
9.31 किसी गैल्वेनोमीटर की कुुंडली से जुड़े समतल दर्पण पर लंबवत आपतित प्रकाश (चित्र 9.33), दर्पण से टकराकर अपना पथ पुनः अनुरेखित करता है| गैल्वेनोमीटर की कुंडली में प्रवाहित कोई धारा दर्पण में 3.5º का परिक्षेपण उत्पन्न करती हैं| दर्पण के सामने 1.5 m दूरी पर रखे परदे पर प्रकाश के परावर्ती चिह्न में कितना विस्थापन होगा?

चित्र 9.33
9.32 चित्र 9.34 में कोई समोत्तल लेंस (अपवर्तनांक 1.50) किसी समतल दर्पण के फलक पर किसी द्रव की परत के संपर्क में दर्शाया गया है| कोई छोटी सुई जिसकी नोंक मुख्य अक्ष पर है, अक्ष के अनुदिश ऊपर-नीचे गति कराकर इस प्रकार समायोजित की जाती है कि सुई की नोंक का उलटा प्रतिबिंब सुई की स्थिति पर ही बने| इस स्थिति में सुई की लेंस से दूरी 45.0 cm है| द्रव को हटाकर प्रयोग को दोहराया जाता है| नयी दूरी 30.0 cm मापी जाती है| द्रव का अपवर्तनांक क्या है?
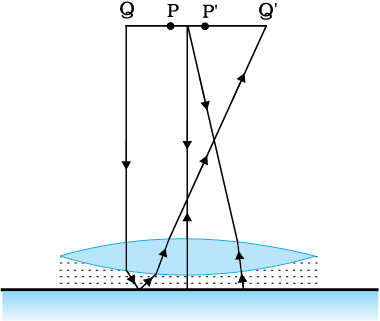
चित्र 9.34