QR12092C10.tif

अध्याय 10

तरंग-प्रकाशिकी

10.1 भूमिका

सन् 1637 में दकार्ते ने प्रकाश के कणिका मॉडल को प्रस्तुत किया तथा स्नेल के नियम को व्युत्पन्न किया| इस मॉडल से किसी अंतरापृष्ठ पर प्रकाश के परावर्तन तथा अपवर्तन के नियमों की व्याख्या की गई है| कणिका मॉडल ने प्रागुक्त किया कि यदि प्रकाश की किरण (अपवर्तन के समय) अभिलंब की ओर मुड़ती है, तब दूसरे माध्यम में प्रकाश की चाल अधिक होगी| आइज़क न्यूटन ने प्रकाश के कणिका सिद्धांत को अपनी प्रसिद्ध पुस्तक अॉपटिक्स (Opticks) में और अधिक विकसित किया| इस पुस्तक की भारी लोकप्रियता के कारण कणिका मॉडल का श्रेय प्रायः न्यूटन को दिया जाता है|

सन् 1678 में डच भौतिकविद क्रिस्टिआन हाइगेंस ने प्रकाश के तरंग सिद्धांत को प्रस्तुत किया– इस अध्याय में हम प्रकाश के इसी तरंग सिद्धांत पर विचार करेंगे| हम देखेंगे कि तरंग मॉडल परावर्तन तथा अपवर्तन की घटनाओं की संतोषप्रद रूप से व्याख्या कर सकता है; तथापि, यह प्रागुक्त करता है कि अपवर्तन के समय यदि तरंग अभिलंब की ओर मुड़ती है तो दूसरे माध्यम में प्रकाश की चाल कम होगी| यह प्रकाश के कणिका मॉडल को उपयोग करते समय की गई प्रागुक्ति के विपरीत है| सन् 1850 में फूको द्वारा किए गए प्रयोग द्वारा दर्शाया गया कि जल में प्रकाश की चाल वायु में प्रकाश की चाल से कम है| इस प्रकार तरंग मॉडल की प्रागुक्ति की पुष्टि की गई|

मुख्यतः न्यूटन के प्रभाव के कारण तरंग सिद्धांत को सहज ही स्वीकार नहीं किया गया| इसका एक कारण यह भी था कि प्रकाश निर्वात में गमन कर सकता है और यह महसूस किया गया कि तरंगों के एक बिंदु से दूसरे बिंदु तक संचरण के लिए सदैव माध्यम की आवश्यकता होती है| तथापि, जब टॉमस यंग ने सन् 1801 में अपना व्यतिकरण संबंधी प्रसिद्ध प्रयोग किया तब यह निश्चित रूप से प्रमाणित हो गया कि वास्तव में प्रकाश की प्रकृति तरंगवत है| दृश्य प्रकाश की तरंगदैर्घ्य को मापा गया और यह पाया गया कि यह अत्यंत छोटी है; उदाहरण के लिए पीले प्रकाश की तरंगदैर्घ्य लगभग 0.6µm है| दृश्य प्रकाश की तरंगदैर्घ्य छोटी होने के कारण (सामान्य दर्पणाें तथा लेंसों के आकार की तुलना में), प्रकाश को लगभग सरल रेखाओं में गमन करता हुआ माना जा सकता है| यह ज्यामितीय प्रकाशिकी का अध्ययन क्षेत्र है, जिसके विषय में हम अध्याय 9 में चर्चा कर चुके हैं| वास्तव में प्रकाशिकी की वह शाखा जिसमें तरंगदैर्घ्य की परिमितता को पूर्ण रूप से नगण्य मानते हैं

ज्यामितीय प्रकाशिकी कहलाती है तथा किरण को ऊर्जा संचरण के उस पथ की भाँति परिभाषित करते हैं जिसमें तरंगदैर्घ्य का मान शून्य की ओर प्रवृत्त होता है|

सन् 1801 में टॉमस यंग द्वारा किए गए व्यतिकरण प्रयोग के पश्चात, आगामी लगभग 40 वर्ष तक प्रकाश तरंगों के व्यतिकरण तथा विवर्तन संबंधी अनेक प्रयोग किए गए| इन प्रयोगों का स्पष्टीकरण केवल प्रकाश के तरंग मॉडल के आधार पर संतोषजनक रूप से किया जा सका है| इस प्रकार उन्नीसवीं शताब्दी के लगभग मध्य तक तरंग सिद्धांत भली-भाँति स्थापित हो गया प्रतीत होता था| सबसे बड़ी कठिनाई उस मान्यता के कारण थी, जिसके अनुसार यह समझा जाता था कि तरंग संचरण के लिए किसी माध्यम की आवश्यकता होती है, तो फिर, प्रकाश तरंगें निर्वात में कैसे संचरित हो सकती हैं| इसकी व्याख्या मैक्सवेल द्वारा प्रकाश संबंधी प्रसिद्ध वैद्युतचुंबकीय सिद्धांत प्रस्तुत करने पर हो पाई| मैक्सवेल ने विद्युत तथा चुंबकत्व के नियमों का वर्णन करने वाले समीकरणों का एक सेट विकसित किया और इन समीकरणों का उपयोग करके उन्होंने तरंग समीकरण व्युत्पन्न किया, जिससे उन्होंने वैद्युतचुंबकीय तरंगों* के अस्तित्व की भविष्यवाणी की| मैक्सवेल तंरग समीकरणों का उपयोग कर मुक्त आकाश में, वैद्युतचुंबकीय तरंगों के वेग की गणना कर पाए और उन्होंने पाया कि तरंग वेग का यह सैद्धांतिक मान, प्रकाश की चाल के मापे गए मान के अत्यंत निकट है| इससे उन्होंने यह निष्कर्ष निकाला कि प्रकाश अवश्य ही वैद्युतचुंबकीय तरंग है, इस प्रकार मैक्सवेल के अनुसार प्रकाश तरंगें परिवर्तनशील विद्युत तथा चुंबकीय क्षेत्रों से संबद्ध हैं| परिवर्तनशील विद्युत क्षेत्र समय तथा दिक्स्थान (आकाश) में परिवर्तनशील चुंबकीय क्षेत्र उत्पन्न करता है तथा परिवर्तनशील चुंबकीय क्षेत्र समय तथा दिक्स्थान में परिवर्तनशील विद्युत क्षेत्र उत्पन्न करता है| परिवर्तनशील विद्युत तथा चुंबकीय क्षेत्र निर्वात में भी वैद्युतचुंबकीय तरंगों (या प्रकाश तरंगों) का संचरण कर सकते हैं|

इस अध्याय में हम सर्वप्रथम हाइगेंस के सिद्धांत के मूल प्रतिपादन पर विचार-विमर्श करेंगे एवं परावर्तन तथा अपवर्तन के नियमों को व्युत्पन्न करेंगे| अनुच्छेद 10.4 तथा 10.5 में हम व्यतिकरण की परिघटना का वर्णन करेंगे जो अध्यारोपण के सिद्धांत पर आधारित है|

हम विवर्तन की परिघटना पर विचार करेंगे जो हाइगेंस-फ्रेनेल सिद्धांत पर आधारित है| अंत में अनुच्छेद 10.7 में हम ध्रुवण के बारे में विचार-विमर्श करेंगे जो इस तथ्य पर आधारित है कि प्रकाश तरंगें अनुप्रस्थ वैद्युतचुंबकीय तरंगें हैं|

* लगभग सन् 1864 में मैक्सवेल ने वैद्युतचुंबकीय तरंगों के अस्तित्व की भविष्यवाणी की; इसके काफ़ी समय पश्चात (लगभग 1890 में) हेनरी हट्ρज़ ने प्रयोगशाला में रेडियो तरंगें उत्पन्न कीं| जगदीश चंद्र बोस तथा मारकोनी ने हर्ट्ज़ की तरंगों का प्रायोगिक उपयोग किया|

क्या प्रकाश सीधी रेखा में चलता है?

कक्षा 6 में प्रकाश सीधी रेखा में चलता है; कक्षा 12 और इससे आगे यह एेसा नहीं करता! क्या आपको आश्चर्य नहीं होता?

विद्यालय में आपको एक प्रयोग दिखलाया गया होगा जिसमें आप बारीक छेद किए हुए तीन गत्ते लेते हैं, एक ओर मोमबत्ती रखकर दूसरी ओर से देखते हैं| यदि मोमबत्ती की ज्वाला तथा तीनों छिद्र एक सीधी रेखा में हैं तो आप मोमबत्ती की ज्वाला देख सकते हैं| इनमें से यदि किसी एक को भी थोड़ा-सा विस्थापित कर दिया जाए तो आप मोमबत्ती की ज्वाला नहीं देख पाते| इसीलिए आपके अध्यापक कहते हैं, यह सिद्ध करता है कि प्रकाश सीधी रेखा में चलता है|

इस पुस्तक में लगातार दो अध्याय (9 तथा 10) हैं, एक किरण प्रकाशिकी पर और दूसरा तरंग प्रकाशिकी पर| किरण प्रकाशिकी प्रकाश के सरल रेखीय संचरण पर आधारित है तथा यह दर्पणों, लेंसों, परावर्तन, अपवर्तन आदि से संबंध रखती है| फिर आप तरंग प्रकाशिकी के अध्याय पर आते हैं और आपको बताया जाता है कि प्रकाश तरंगों के रूप में चलता है, यह वस्तुओं के किनाराें पर मुड़ सकता है, इसमें विवर्तन तथा व्यतिकरण जैसी परिघटनाएँ हो सकती हैं|

प्रकाशिक क्षेत्र में, प्रकाश की तरंगदैर्घ्य लगभग आधा माइक्रोमीटर होती है| यदि इसके रास्ते में लगभग इसी आकार का कोई अवरोध आता है तो यह इसके इधर-उधर मुड़ सकता है और दूसरी ओर दिखलाई दे सकता है| इस प्रकार माइक्रोमीटर आकार का कोई अवरोध प्रकाश किरण को नहीं रोक पाएगा| यदि अवरोध बहुत बड़ा है, तब प्रकाश इसके इधर-उधर इस प्रकार नहीं मुड़ पाएगा और दूसरी ओर दिखलाई नहीं देगा|

यह तरंगों का एक सामान्य गुण है और ध्वनि तरंगों में भी देखा जा सकता है| हमारी वाणी की ध्वनि तरंग की तरंगदैर्घ्य लगभग 50 से.मी. से 1 मी. तक होती है| यदि इसके मार्ग में कुछ मीटर आकार का कोई अवरोध आता है तो यह इसके इधर-उधर मुड़ जाती है तथा अवरोध के पीछे पहुँच जाती है| लेकिन यदि इसके रास्ते में कोई बड़ा अवरोध (लगभग 100 मीटर से अधिक) जैसे कोई पहाड़ी आदि, आती है तो इसका अधिकांश भाग परावर्तित हो जाता है और प्रतिध्वनि के रूप में सुनाई देता है|

तब प्राथमिक विद्यालय में किए गए प्रयोग का क्या हुआ? जब हम वहाँ पर किसी भी गत्ते को खिसकाते हैं तो इसका विस्थापन कुछ मिलीमीटर की कोटि का होता है, जो प्रकाश की तरंगदैर्घ्य से बहुत अधिक है| अतः मोमबत्ती की ज्वाला दिखलाई नहीं देगी| यदि हम किसी भी गत्ते को एक माइक्रोमीटर या इससे भी कम दूरी तक विस्थापित कर सकें तो प्रकाश का विवर्तन हो पाएगा तथा मोमबत्ती की ज्वाला दिखलाई देती रहेगी|

इस बॉक्स के पहले वाक्य में आप जोड़ सकते हैं : बड़े होने पर यह सीखता है कि मुड़ा कैसे जाए!

10.2 हाइगेंस का सिद्धांत

सर्वप्रथम हम तरंगाग्र को परिभाषित करेंगे| जब हम किसी शांत जल के तालाब में एक छोटा पत्थर फेंकते हैं तब प्रतिघात बिंदु से चारों ओर तरंगें फैलती हैं| पृष्ठ का प्रत्येक बिंदु समय के साथ दोलन करना प्रारंभ कर देता है| किसी एक क्षण पर पृष्ठ का फ़ोटोग्राफ़ उन वृत्ताकार वलयों को दर्शाएगा जिनके ऊपर विक्षोभ अधिकतम हैं| स्पष्टतः इस प्रकार के वृत्त के सभी बिंदु समान कला में दोलन करते हैं क्योंकि वे स्रोत से समान दूरी पर हैं| समान कला में दोलन करते एेसे सभी बिंदुओं का बिंदु पथ तरंगाग्र कहलाता है| अतः एक तरंगाग्र को एक समान कला के पृष्ठ के रूप में परिभाषित किया जाता है| जिस गति के साथ तरंगाग्र स्रोत से बाहर की ओर बढ़ता है, वह तरंग की चाल कहलाती है| तरंग की ऊर्जा तरंगाग्र के लंबवत चलती है|

चित्र 10.1 (a) एक बिंदु-स्रोत से निर्गमन होती एक अपसरित गोलीय तरंग| तरंगाग्र गोलीय है|

चित्र 10.1 (b) स्रोत से बहुत अधिक दूरी पर, गोलीय तरंग का एक छोटा भाग समतल तरंग माना जा सकता है|

चित्र 10.2 F₁F₂गोलीय तरंगाग्र को t = 0 समय पर निरूपित करता है (O केंद्र के साथ)|

F1F2 से निर्गमन होने वाली द्वितीयक तरंगिकाओं का आवरण आगे बढ़ते हुए तरंगाग्र

G1G2 को उत्पन्न करता है| पश्च तरंग

D1D2 विद्यमान नहीं होती|

यदि एक बिंदु-स्रोत प्रत्येक दिशा में एक समान तरंगें उत्सर्जित करता है तो उन बिंदुओं का बिंदुपथ, जिनका आयाम समान है और जो एक समान कला में कंपन करते हैं, गोला होता है तथा हमें चित्र 10.1 (a) की भाँति एक गोलीय तरंग प्राप्त होती है| स्रोत से बहुत अधिक दूरी पर, गोले का एक छोटा भाग समतल माना जा सकता है और हमें एक समतल तरंग प्राप्त होती है
[चित्र 10.1 (b)]|

अब यदि हमें t = 0 पर किसी तरंगाग्र की आकृति ज्ञात है तो हाइगेंस के सिद्धांत द्वारा हम किसी बाद के समय τ पर तरंगाग्र की आकृति ज्ञात कर सकते हैं| अतः हाइगेंस का सिद्धांत वास्तव में एक ज्यामितीय रचना है जो किसी समय यदि तरंगाग्र की आकृति दी हुई हो तो किसी बाद के समय पर हम तरंगाग्र की आकृति ज्ञात कर सकते हैं| आइए, एक अपसरित तरंग के बारे में विचार करें और मान लीजिए F₁F₂, t = 0 समय पर एक गोलीय तरंगाग्र के एक भाग को प्रदर्शित करता है (चित्र 10.2)| अब हाइगेंस के सिद्धांत के अनुसार, तरंगाग्र का प्रत्येक बिंदु एक द्वितीयक विक्षोभ का स्रोत है और इन बिंदुओं से होने वाली तरंगिकाएँ तरंग की गति से सभी दिशाओं में फैलती हैं| तरंगाग्र से निर्गमन होने वाली इन तरंगिकाओं को प्रायः द्वितीयक तरंगिकाओं के नाम से जाना जाता है और यदि हम इन सभी गोलों पर एक उभयनिष्ठ स्पर्शक पृष्ठ खींचें तो हमें किसी बाद के समय पर तरंगाग्र की नयी स्थिति प्राप्त हो जाती है|

चित्र 10.3 दाईं ओर संचरित होने वाली एक समतल तरंग के लिए हाइगेंस का ज्यामितीय निर्माण| F1 F2,

t = 0 पर एक समतल तरंगाग्र है तथा G1G2 τ समय बाद का एक तरंगाग्र है| रेखाएँ A1A2, B1B2 … आदि F1F2 तथा G1G2 दोनों के लंबवत हैं तथा किरणों को निरूपित करती हैं|

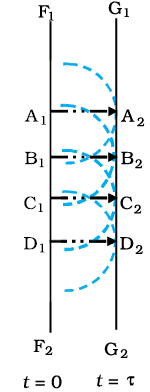
अतः यदि हम t = τ समय पर तरंगाग्र की आकृति ज्ञात करना चाहते हैं तो हम गोलीय तरंगाग्र के प्रत्येक बिंदु से vτ त्रिज्या के गोले खींचेंगे, जहाँ पर v माध्यम में तरंग की चाल को निरूपित करता है| यदि हम इन सभी गोलों पर एक उभयनिष्ठ स्पर्श रेखा खींचें, तो हमें t = τ समय पर तरंगाग्र की नयी स्थिति प्राप्त होगी| चित्र 10.2 में G1 G2 द्वारा प्रदर्शित नया तरंगाग्र पुनः गोलीय है जिसका केंद्र O है|

उपरोक्त मॉडल में एक दोष है| हमें एक पश्च तरंग भी प्राप्त होती है जिसे चित्र 10.2 में D1D2 द्वारा दर्शाया गया है| हाइगेंस ने तर्क प्रस्तुत किया कि आगे की दिशा में द्वितीयक तरंगिकाओं का आयाम अधिकतम होता है तथा पीछे की दिशा में यह शून्य होता है| इस तदर्थ कल्पना से हाइगेंस पश्च तरंगों की अनुपस्थिति को समझा पाए| तथापि यह तदर्थ कल्पना संतोषजनक नहीं है तथा पश्चतरंगों की अनुपस्थिति का औचित्य वास्तव में एक अधिक परिशुद्ध तरंग सिद्धांत द्वारा बताया जा सकता है|

इसी विधि द्वारा हम हाइगेंस के सिद्धांत का उपयोग किसी माध्यम में संचरित होने वाली समतल तरंग के तरंगाग्र की आकृति ज्ञात करने के लिए कर सकते हैं (चित्र 10.3)|

Huygens.tif

क्रिस्टिआन हाइगेंस (1629-1695) डच भौतिकविद खगोल- शास्त्री, गणितज्ञ एवं प्रकाश के तरंग सिद्धांत के प्रणेता| उनकी पुस्तक ट्रीटीज अॉन लाइट (Treatise on light), आज भी पढ़ने में अच्छी लगती है| इस पुस्तक में परावर्तन और अपवर्तन के अतिरिक्त, खनिज कैलसाइट द्वारा प्रदर्शित दोहरे- अपवर्तन की प्रक्रिया को भी बहुत सुंदर ढंग से समझाया गया है| वही पहले व्यक्ति थे जिन्होंने वृत्तीय गति एवं सरल-आवर्त गति का विश्लेषण प्रस्तुत किया और सुधरी हुई घड़ियाँ एवं टेलिस्कोप बनाए| उन्होंने शनि-वलयों की सही ज्यामिति प्रस्तुत की|

10.3 हाइगेंस सिद्धांत का उपयोग करते हुए समतल तरंगों का अपवर्तन तथा परावर्तन

10.3.1 समतल तरंगों का अपवर्तन

अब हम हाइगेंस के सिद्धांत का उपयोग अपवर्तन के नियमों को व्युत्पन्न करने के लिए करेंगे| मान लीजिए PP′ माध्यम 1 तथा माध्यम 2 को पृथक करने वाले पृष्ठ को निरूपित करता है (चित्र 10.4)| मान लीजिए v1 तथा v2 क्रमशः माध्यम 1 तथा माध्यम 2 में प्रकाश की चाल को निरूपित करते हैं| हम मान लेते हैं कि एक समतल तरंगाग्र AB, A′A दिशा में संचरित होता हुआ चित्र में दर्शाए अनुसार अंतरापृष्ठ पर कोण i बनाते हुए आपतित होता है| मान लीजिए BC दूरी चलने के लिए तरंगाग्र द्वारा लिया गया समय τ है| अतः

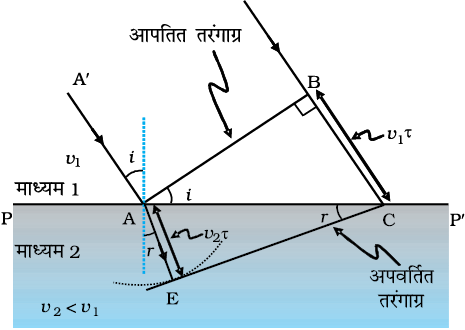
चित्र 10.4 एक समतल तरंगाग्र AB माध्यम 1 तथा माध्यम 2 को पृथक करने वाले पृष्ठ PP′ पर कोण i बनाते हुए आपतित होता है| समतल तरंगाग्र अपवर्तित होता है तथा CE अपवर्तित तरंगाग्र को निरूपित करता है| चित्र v2 < v1 के तदनुरूप है, अतः अपवर्तित तरंगें अभिलंब की ओर मुड़ती हैं|

BC = v1 τ

अपवर्तित तरंगाग्र की आकृति ज्ञात करने के लिए हम बिंदु A से v2τ त्रिज्या का एक गोला दूसरे माध्यम में खींचते हैं (दूसरे माध्यम में तरंग की चाल v2 है)| मान लीजिए CE बिंदु C से गोले पर खींचे गए स्पर्शी तल को निरूपित करता है| तब, AE = v2 τ तथा CE अपवर्तित तरंगाग्र को निरूपित करेगी| अब यदि हम त्रिभुज ABC तथा AEC पर विचार करें तो हमें प्राप्त होगा

sin i = 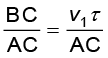(10.1)

और

sin r = 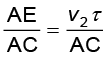(10.2)

यहाँ i और r क्रमशः आपतन कोण तथा अपवर्तन कोण हैं| अतः हमें प्राप्त होगा

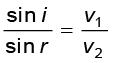(10.3)

उपरोक्त समीकरण से हमें एक महत्वपूर्ण परिणाम प्राप्त होता है| यदि r < i (अर्थात, यदि किरण अभिलंब की ओर मुड़ती है), तो दूसरे माध्यम में प्रकाश तरंग की चाल (v2) पहले माध्यम में प्रकाश तरंग की चाल (v1) से कम होगी| यह प्रागुक्ति प्रकाश के कणिका मॉडल की प्रागुक्ति के विपरीत है और जैसा कि बाद के प्रयोगों ने दर्शाया, तरंग सिद्धांत की प्रागुक्ति सही है| अब यदि c निर्वात में प्रकाश की चाल को निरूपित करती है, तब,

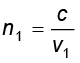(10.4)

तथा

n2 = 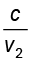(10.5)

n1 तथा n2, क्रमशः माध्यम 1 तथा माध्यम 2 के अपवर्तनांक हैं| अपवर्तनांकों के रूप में समीकरण (10.3) को निम्न प्रकार से लिख सकते हैं

n1 sin i = n2 sin r (10.6)

यह स्नैल का अपवर्तन संबंधी नियम है| यदि λ1 तथा λ 2 क्रमशः माध्यम 1 तथा माध्यम 2 में प्रकाश की तरंगदैर्घ्य को निरूपित करते हैं और यदि दूरी BC, λ 1 के बराबर है तब दूरी AE, λ 2 के बराबर होगी (क्योंकि यदि कोई शृंग B से C तक τ समय में पहुँचता है तो वह शृंग A से E तक भी τ समय में ही पहुँचेगा); अतः

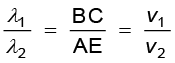
अथवा

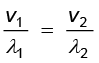(10.7)

उपरोक्त समीकरण में अंतर्निहित है कि जब तरंग सघन माध्यम में अपवर्तित होती है (v1 > v2), तो तरंगदैर्घ्य तथा संचरण की चाल कम हो जाती है, लेकिन आवृत्ति ν (= v/λ) उतनी ही रहती है|

10.3.2 विरल माध्यम पर अपवर्तन

आइए, एक समतल तरंग के विरल माध्यम में होने वाले अपवर्तन पर विचार करें, अर्थात v2 > v1| पहले की भाँति ही कार्यवाही करते हुए हम चित्र 10.5 में दर्शाए अनुसार अपवर्तित तरंगाग्र का निर्माण कर सकते हैं| अब अपवर्तन कोण आपतन कोण से बड़ा होगा; तथापि इस बार भी n₁ sin_i= n2 sin r | हम एक कोण ic को निम्न समीकरण द्वारा परिभाषित कर सकते हैं

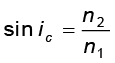(10.8)

अतः, यदि i = ic तब sin r = 1 तथा r = 90°| स्पष्टतया, i > ic के लिए कोई भी अपवर्तित तरंग प्राप्त नहीं होगी| कोण ic को क्रांतिक कोण कहते हैं तथा क्रांतिक कोण से अधिक सभी आपतन कोणों के लिए हमें कोई भी अपवर्तित तरंग प्राप्त नहीं होगी तथा तरंग का पूर्ण आंतरिक परावर्तन हो जाएगा| पूर्ण आंतरिक परावर्तन की परिघटना तथा इसके अनुप्रयोगों की परिचर्चा अनुच्छेद 9.4 में की गई थी|

10.3.3 समतल पृष्ठ से एक समतल तरंग का परावर्तन

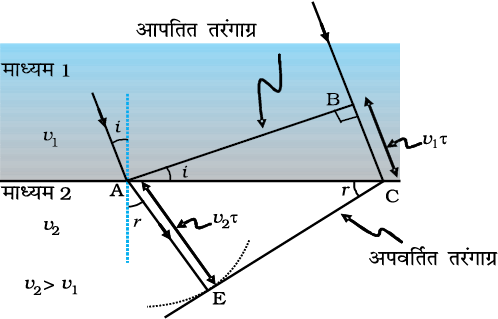
चित्र 10.5 विरल माध्यम जिसके लिए v2 > v1 पर आपतित एक समतल तरंग का अपवर्तन| समतल तरंग अभिलंब से दूर मुड़ जाती है|

अब हम एक परावर्तक पृष्ठ MN पर किसी कोण i से आपतित एक समतल तरंग AB पर विचार करते हैं| यदि v माध्यम में तरंग की चाल को निरूपित करता है तथा यदि τ तरंगाग्र द्वारा बिंदु B से C तक आगे बढ़ने में लिए गए समय को निरूपित करता है, तब दूरी

BC= vτ

परावर्तित तरंगाग्र का निर्माण करने के लिए हम बिंदु A से त्रिज्या v τ का गोला खींचते हैं (चित्र 10.6)| मान लीजिए CE इस गोले पर बिंदु C से खींची गई स्पर्शी समतल को निरूपित करती है| स्पष्टतया

चित्र 10.6 परावर्तक पृष्ठ MN द्वारा समतल तरंग AB का परावर्तन| AB तथा CE क्रमशः आपतित तथा परावर्तित तरंगाग्र को निरूपित करती हैं|

AE = BC = vτ

अब यदि हम त्रिभुजों EAC तथा BAC पर विचार करें तो हम पाएँगे कि ये सर्वांगसम हैं और इसीलिए, कोण i तथा r बराबर होंगे (चित्र 10.6)| यह परावर्तन का नियम है|

एक बार परावर्तन तथा अपवर्तन के नियमों को जान लेने के पश्चात प्रिज़्मों, लेंसों तथा दर्पणों के व्यवहार को समझा जा सकता है| इस परिघटना की प्रकाश के सरल रेखीय पथ पर गमन करने के आधार पर अध्याय 9 में विस्तार से चर्चा की गई थी| यहाँ हम केवल परावर्तन तथा अपवर्तन के समय तरंगाग्रों के व्यवहार का वर्णन करेंगे| चित्र 10.7(a) में हम एक पतले प्रिज़्म से गुज़रने वाली समतल तरंग पर विचार करते हैं| स्पष्टतया, क्योंकि काँच में प्रकाश तरंगों की चाल कम है, अंदर आते हुए तरंगाग्र का निचला भाग (जो काँच की अधिकतम मोटाई को पार करता है) सबसे अधिक विलंबित होगा| इसके परिणामस्वरूप प्रिज़्म से बाहर निकलने वाली तरंगाग्र चित्र में दर्शाए अनुसार झुक जाएगा| चित्र 10.7(b) में हम एक पतले उत्तल लेंस पर आपतित होने वाली समतल तरंग पर विचार करते हैं| आपतित समतल तरंग का मध्य भाग लेंस के सबसे मोटे भाग से होकर जाता है तथा सर्वाधिक विलंबित होता है| लेंस से बाहर निकलने वाले तरंगाग्र में केंद्र पर अवनमन होता है और इसीलिए तरंगाग्र गोलीय हो जाता है तथा एक बिंदु F पर अभिसरित होता है जिसे फ़ोकस कहते हैं| चित्र 10.7(c) में एक अवतल दर्पण पर एक समतल तरंग आपतित होती है तथा परावर्तन पर हमें एक गोलीय तरंग प्राप्त होती है जो फ़ोकस बिंदु F पर अभिसरित होती है| इसी प्रकार हम अवतल लेंसों तथा उत्तल दर्पणों द्वारा अपवर्तन तथा परावर्तन को समझ सकते हैं|

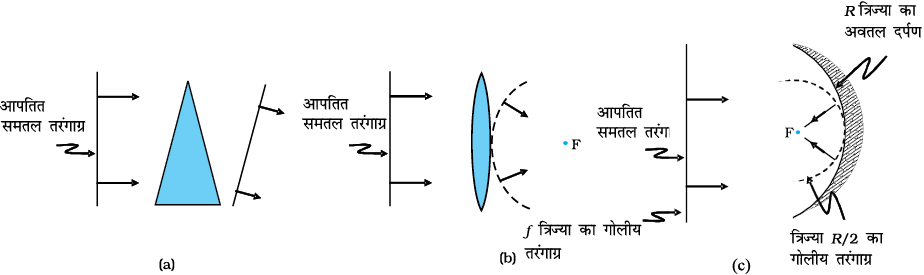
चित्र 10.7 एक समतल तरंगाग्र का अपवर्तन (a) एक पतले प्रिज़्म द्वारा, (b) एक उत्तल लेंस द्वारा,

उपरोक्त विवेचन से यह ज्ञात होता है कि वस्तु पर किसी बिंदु से प्रतिबिंब के संगत बिंदु तक लगा कुल समय एक ही होता है, चाहे जिस भी किरण के अनुदिश मापा जाए| उदाहरण के लिए, जब कोई उत्तल लेंस, प्रकाश को एक वास्तविक प्रतिबिंब बनाने के लिए फ़ोकस करता है तो यद्यपि केंद्र से होकर जाने वाली किरणें छोटा पथ तय करती हैं, लेकिन काँच में धीमी चाल के कारण लगने वाला समय उतना ही होता है जितना कि लेंस के किनारे के निकट से होकर चलने वाली किरणों के लिए होता है|

10.3.4 डॉप्लर प्रभाव

हम यहाँ कहना चाहेंगे कि तरंगाग्रों का निर्माण करते समय यदि स्रोत (अथवा प्रेक्षक) गतिमान हों तो हमें सावधानी बरतनी चाहिए| उदाहरण के लिए, यदि कोई माध्यम न हो तथा स्रोत प्रेक्षक से दूर रहा हो तब बाद के तरंगाग्रों को प्रेक्षक तक पहुँचने में अधिक दूर चलना पड़ता है और इसलिए वे अधिक समय लेते हैं| इस प्रकार दो उत्तरोत्तर तरंगाग्रों के प्रेक्षक तक पहुँचने में लगने वाला समय स्रोत तक उनके पहुँचने में लगने वाले समय की अपेक्षा अधिक होता है| अतः जब स्रोत प्रेक्षक से दूर जाता है तो प्रेक्षक द्वारा मापी जाने वाली आवृत्ति में कमी होगी| यह डॉप्लर प्रभाव कहलाता है| खगोलज्ञ, तरंगदैर्घ्य में डॉप्लर प्रभाव के कारण होने वाली इस वृद्धि को अभिरक्त विस्थापन (red shift) कहते हैं, क्योंकि, स्पेक्ट्रम के दृश्य क्षेत्र की मध्यवर्ती तरंगदैर्घ्य लाल छोर की ओर खिसक जाती है| जब स्रोत प्रेक्षक की ओर चलता है तो उससे प्राप्त की जाने वाली तरंगों की तरंगदैर्घ्य में आभासी कमी हो जाती है, तरंगदैर्घ्य की इस कमी को नीला विस्थापन (blue shift) कहते हैं|

आपने पहले ही कक्षा 11 की पाठ्यपुस्तक के अध्याय 15 में ध्वनि तरंगों में डॉप्लर प्रभाव का अध्ययन किया है| प्रकाश की चाल की तुलना में कम वेगों के लिए हम उन्हीं सूत्रों का प्रयोग कर सकते हैं, जिनका प्रयोग ध्वनि तरंगों के लिए किया जाता है| आवृत्ति में भिन्नात्मक परिवर्तन ∆ν/ν को –vत्रिज्य/c के द्वारा दिया जाता है, जहाँ vत्रिज्य प्रेक्षक के सापेक्ष स्रोत-वेग का प्रेक्षक को स्रोत से जोड़ने वाली रेखा की दिशा में घटक है| जब स्रोत प्रेक्षक से दूर जाता है, vत्रिज्य को धनात्मक मानते हैं| इस प्रकार डॉप्लर विस्थापन को व्यक्त कर सकते हैं –

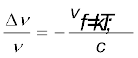(10.9)

उपरोक्त सूत्र तभी मान्य है जब स्रोत का वेग प्रकाश के वेग की तुलना में कम होता है| डॉप्लर प्रभाव का अधिक यथार्थ सूत्र प्राप्त करने के लिए, जो उन चालों के लिए भी मान्य है जो प्रकाश की चाल के निकट होती हैं, आइंसटाइन के सापेक्षिकता के विशिष्ट सिद्धांत की आवश्यकता होती है| प्रकाश के लिए डॉप्लर प्रभाव खगोलशास्त्र में बहुत महत्वपूर्ण है| यह दूरस्थ गैलेक्सियों के त्रिज्य-वेगों के मापन का आधार है|

उदाहरण 10.1 हमारे सापेक्ष किसी गैलेक्सी को किस गति से चलना चाहिए जिससे कि 589.0 nm की सोडियम लाइन 589.6 nm पर प्रेक्षित हो?

हल क्योंकि νλ = c, 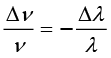(ν तथा λ में कम परिवर्तनों के लिए)

∆λ = 589.6 – 589.0 = + 0.6 nm

समीकरण (10.9) के उपयोग से हम पाते हैं,

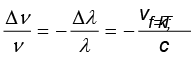
अथवा vत्रिज्य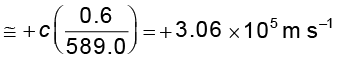

= 306 km/s

अतः गैलेक्सी इस गति से हमसे दूर जा रही है|

उदाहरण 10.2

(a) जब एकवर्णीय प्रकाश दो माध्यमों को पृथक करने वाली सतह पर आपतित होता है, तब परावर्तित एवं अपवर्तित दोनों प्रकाश की आवृत्तियाँ समान होती हैं| स्पष्ट कीजिए क्यों?

(b) जब प्रकाश विरल से सघन माध्यम में गति करता है तो उसकी चाल में कमी आती है| क्या चाल में आई कमी प्रकाश तरंगों द्वारा संचारित ऊर्जा की कमी को दर्शाती है?

(c) प्रकाश की तरंग अवधारणा में, प्रकाश की तीव्रता का आकलन तरंग के आयाम के वर्ग से किया जाता है| वह क्या है जो प्रकाश की फ़ोटॉन अवधारणा में प्रकाश की तीव्रता का निर्धारण करता है?

हल

(a) परावर्तन तथा अपवर्तन, आपतित प्रकाश की पदार्थ के परमाणवीय अवयवों के साथ अन्योन्य क्रिया के द्वारा हो पाता है| परमाणुओं को दोलित्र के रूप में देखा जा सकता है जो बाह्य साधन

(प्रकाश) की आवृत्ति को लेकर प्रणोदित दोलन कर सकते हैं| एक आवेशित दोलक द्वारा उत्सर्जित प्रकाश की आवृत्ति उसके दोलन की आवृत्ति के बराबर होती है| अतः विकिरित प्रकाश की आवृत्ति आपतित प्रकाश की आवृत्ति के बराबर होती है|

(b) नहीं| तरंग द्वारा ले जाने वाली ऊर्जा तरंग के आयाम पर निर्भर करती है, यह तरंग संचरण की चाल पर निर्भर नहीं करती|

(c) फ़ोटॉन चित्रण में किसी दी हुई आवृत्ति के लिए प्रकाश की तीव्रता एकांक क्षेत्रफल से एकांक समय में गमन करने वाले फ़ोटॉन की संख्या द्वारा निर्धारित होती है|

10.4 तरंगों का कला-संबद्ध तथा कला-असंबद्ध योग

इस अनुच्छेद में हम दो तरंगों के अध्यारोपण द्वारा उत्पन्न व्यतिकरण के चित्राम (पैटर्न) पर विचार-विमर्श करेंगे| आपको याद होगा, हमने कक्षा 11 की पाठ्यपुस्तक के अध्याय 15 में अध्यारोपण के सिद्धांत का विवेचन किया था| वास्तव में व्यतिकरण का समस्त क्षेत्र अध्यारोपण के सिद्धांत पर आधारित है, जिसके अनुसार किसी माध्यम में एक विशिष्ट बिंदु पर अनेक तरंगों द्वारा उत्पन्न परिणामी विस्थापन इनमें से प्रत्येक तरंग के विस्थापनों का सदिश योग होता है|

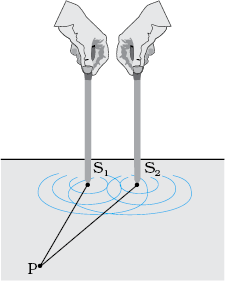
(a)

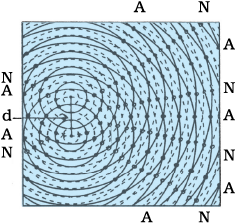
(b)

चित्र 10.8 (a) जल में समान कला में कंपन करती दो सुइयाँ दो संबद्ध स्रोतों को निरूपित करती हैं|

(b) जल के पृष्ठ पर किसी समय पर जल के अणुओं के विस्थापन का पैटर्न जिसमें निस्पंदी (शून्य विस्थापन) तथा प्रस्पंदी (अधिकतम विस्थापन) रेखाएँ दर्शायी गई हैं|

दो सुइयों S1 तथा S2 की कल्पना करें जो जल की एक द्रोणिका में ऊपर और नीचे समान आवर्ती गति कर रही हैं [चित्र 10.8 (a)]| वे जल की दो तरंगें उत्पन्न करती हैं तथा किसी विशिष्ट बिंदु पर, प्रत्येक तरंग द्वारा उत्पन्न विस्थापनों के बीच कलांतर समय के साथ नहीं बदलता| जब एेसा होता है तो इन दो स्रोतों को कला-संबद्ध कहा जाता है| चित्र 10.8 (b) में किसी दिए हुए समय पर शृंग (सतत वृत्त) तथा गर्त (बिंदुकित वृत्त) दर्शाए गए हैं| एक बिंदु P पर विचार करें जिसके लिए

S₁ P = S₂ P

क्योंकि दूरियाँ S₁ P तथा S₂P बराबर हैं, इसलिए S₁ तथा S₂ से तरंगें P बिंदु तक चलने में समान समय लेंगी तथा जो तरंगें S₁ तथा S₂से समान कला में निर्गम होती हैं, वे P बिंदु पर भी समान कला में पहुँचेंगी|

इस प्रकार, यदि स्रोत S1 द्वारा किसी बिंदु P पर उत्पन्न विस्थापन

y1 = a cos ωt

द्वारा दिया गया है तो स्रोत S2 द्वारा उत्पन्न विस्थापन (बिंदु P पर) भी

y2 = a cos ωt

द्वारा प्रदर्शित होगा| अतः परिणामी विस्थापन होगा

y = y1 + y2 = 2 a cos ωt

क्योंकि तीव्रता विस्थापन के वर्ग के समानुपातिक है, इसलिए परिणामी तीव्रता होगी

I = 4 I0

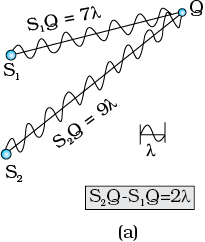
जहाँ I0 प्रत्येक स्रोत की पृथक तीव्रता को निरूपित करती है| हम देख रहे हैं कि I0, a2 के समानुपाती है| वास्तव में S1S2 के लंबअर्धक के किसी भी बिंदु पर तीव्रता 4I0 होगी| दोनों स्रोतों को रचनात्मक रूप से व्यतिकरण करते हुए कहा जाता है और इसे हम संपोषी व्यतिकरण कहते हैं| अब हम बिंदु Q पर विचार करते हैं [चित्र 10.9(a)], जिसके लिए

S2Q –S1Q = 2λ

S1 से निर्गमित तरंगें S2 से आने वाली तरंगों की अपेक्षा ठीक दो चक्र पहले पहुँचती हैं तथा फिर से समान कला में होंगी [चित्र 10.9 (a)]| यदि S1 द्वारा उत्पन्न विस्थापन

y1 = a cos ωt

चित्र 10.9

(a) बिंदु Q पर संपोषी व्यतिकरण जिसके लिए पथांतर 2λ है| (b) बिंदु R पर विनाशी व्यतिकरण जिसके लिए पथांतर 2.5 λ है |

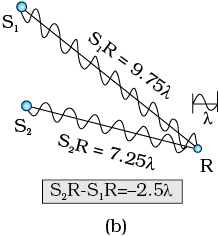
चित्र 10.10 उन बिंदुओं का बिंदुपथ जिनके लिए S₁P – S₂P शून्य, ±λ, ± 2λ, ± 3λ हैं|

हो तो S2 द्वारा उत्पन्न विस्थापन

y2 = a cos (ωt – 4π) = a cos ωt होगा|

यहाँ हमने इस तथ्य का उपयोग किया है कि 2λ का पथांतर 4π के कलांतर के संगत है|

दोनों विस्थापन फिर से समान कला में हैं तथा तीव्रता फिर 4 I0 होगी और इससे संपोषी व्यतिकरण होगा| उपरोक्त विश्लेषण में हमने यह मान लिया है कि दूरियाँ S1Q तथा S2Q, d (जो S1 तथा S2 के बीच दूरी निरूपित करता है) की अपेक्षा बहुत अधिक हैं, अतएव यद्यपि S1Q तथा S2Q समान नहीं हैं, प्रत्येक तरंग द्वारा उत्पन्न विस्थापन का आयाम लगभग समान है|

अब हम एक बिंदु R पर विचार करते हैं [चित्र 10.9(b)] जिसके लिए

S₂R – S₁R = –2.5λ

S₁ से निर्गमित तरंगें स्रोत S2 से आने वाली तरंगों की अपेक्षा 2.5 चक्र बाद पहुँचती हैं [चित्र 10.10(b)]| अतः यदि स्रोत S₁ द्वारा उत्पन्न विस्थापन का मान है

y1 = a cos ωt

तब स्रोत S2 द्वारा उत्पन्न विस्थापन

y2 = a cos (ωt + 5π) = – a cos ωt होगा|

यहाँ हमने इस तथ्य का उपयोग किया है कि 2.5λ का पथांतर 5π के कलांतर के संगत है| दोनों विस्थापन अब विपरीत कलाओं में हैं तथा दोनों विस्थापन एक-दूसरे को रद्द कर देते हैं तथा शून्य तीव्रता प्राप्त होती है| इसे विनाशी व्यतिकरण कहते हैं|

सारांशतः यदि दो संबद्ध स्रोत S₁ तथा S₂ समान कला में कंपन कर रहे हैं तब किसी यथेच्छ बिंदु P के लिए जबकि पथांतर

S1P ~ S2P = nλ (n = 0, 1, 2, 3,...) (10.10)

हमें संपोषी व्यतिकरण प्राप्त होगा तथा परिणामी तीव्रता 4I0 होगी| S1P तथा S2 P के बीच चिह्न (~) S1P तथा S2 P के बीच अंतर को निरूपित करता है| दूसरी ओर यदि बिंदु P इस प्रकार है कि पथांतर,

S1P ~ S2P = (n+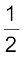) λ (n = 0, 1, 2, 3, ...) (10.11)

तो हमें विनाशी व्यतिकरण प्राप्त होगा तथा परिणामी तीव्रता शून्य होगी| अब, किसी दूसरे यथेच्छ बिंदु G (चित्र 10.10) के लिए मान लीजिए दो विस्थापनों के बीच कलांतर φ है; तब यदि स्रोत S1 द्वारा उत्पन्न विस्थापन

y1 = a cos ωt

हो तो स्रोत S2 द्वारा उत्पन्न विस्थापन

y2 = a cos (ωt + φ) होगा

तथा परिणामी विस्थापन होगा

y = y1 + y2

= a [cos ωt + cos (ωt +φ)]

= 2 a cos (φ/2) cos (ωt + φ/2)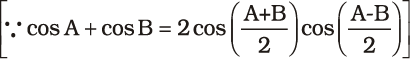

परिणामी विस्थापन का आयाम 2a cos (φ/2) है इसलिए उस बिंदु पर तीव्रता होगी

I = 4 I0 cos2 (φ/2) (10.12)

यदि φ = 0, ± 2 π, ± 4 π,… जो समीकरण (10.10) की शर्त के संगत है, हमें संपोषी व्यतिकरण प्राप्त होगा तथा तीव्रता अधिकतम होगी| दूसरी ओर यदि φ = ± π, ± 3π, ± 5π … [जो समीकरण (10.11) की शर्त के संगत है] हमें विनाशी व्यतिकरण प्राप्त होगा तथा तीव्रता शून्य होगी|

अब यदि दो स्रोत कला-संबद्ध हैं (अर्थात इस प्रयोग में यदि दोनों सुइयाँ नियमित रूप से ऊपर नीचे आ-जा रही हैं) तो किसी भी बिंदु पर कलांतर φ समय के साथ नहीं बदलेगा तथा हमें स्थिर व्यतिकरण पैटर्न प्राप्त होगा, अर्थात् समय के साथ उच्चिष्ठ (maxima) तथा निम्निष्ठ (minima) की स्थितियाँ नहीं बदलेंगी| तथापि, यदि दोनों सुइयाँ निश्चित कलांतर नहीं रख पाती हैं, तो समय के साथ व्यतिकरण पैटर्न भी बदलेगा तथा यदि कलांतर समय के साथ बहुत तेज़ी से बदलता है, तो उच्चिष्ठ तथा निम्निष्ठ की स्थितियाँ भी समय के साथ तेज़ी से बदलेंगी तथा हम ‘काल औसत’ तीव्रता वितरण देखेंगे| जब एेसा होता है तो हमें औसत तीव्रता प्राप्त होगी, जिसका मान होगा

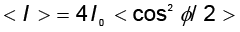(10.13)

जहाँ कोणीय कोष्ठक काल औसत निरूपित करते हैं| वास्तव में अनुच्छेद 7.2 में दर्शाया गया है कि यदि φ(t) समय के साथ यादृच्छिक रूप से बदलता है तो काल औसत राशि < cos2 (φ/2) > का मान 1/2 होगा| यह भी सहजानुभूति से स्पष्ट है, क्योंकि फलन cos2 (φ/2) यादृच्छिक रूप से 0 तथा 1 के बीच बदलेगा तथा औसत मान 1/2 होगा| सभी बिंदुओं पर परिणामी तीव्रता निम्न से प्राप्त होगी

I = 2 I0 (10.14)

जब समय के साथ दो कंपित स्रोतों का कलांतर तेज़ी से बदलता है, हम कहते हैं कि ये स्रोत कला-असंबद्ध हैं और जब एेसा होता है तो तीव्रताएँ केवल जुड़ जाती हैं| वास्तव में एेसा तब होता है जब दो अलग-अलग प्रकाश स्रोत किसी दीवार को प्रकाशित करते हैं|

10.5 प्रकाश तरंगों का व्यतिकरण तथा यंग का प्रयोग

अब हम प्रकाश तरंगों का उपयोग करके व्यतिकरण पर विचार करेंगे| यदि हम दो सूचिछिद्रों को प्रदीप्त करने के लिए दो सोडियम लैंपों का उपयोग करें (चित्र 10.11), तो हमें कोई व्यतिकरण फ्रिंज दिखाई नहीं देंगी| एेसा इस तथ्य के कारण है कि एक सामान्य स्रोत (जैसे सोडियम लैंप) से उत्सर्जित होने वाली प्रकाश तरंगों में, 10–10 s की कोटि के समय अंतरालों पर, आकस्मिक कला-परिवर्तन होता है| अतः दो स्वतंत्र प्रकाश स्रोतों से आने वाली प्रकाश तरंगों में कोई निश्चित कला संबंध नहीं होता तथा ये कला-असंबद्ध होते हैं| जैसी कि पहले अनुच्छेद में विवेचना की जा चुकी है, एेसा होने पर परदे पर तीव्रताएँ जुड़ जाती हैं|

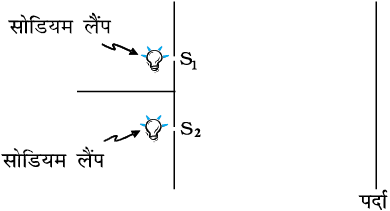
इंग्लैंड के भौतिकशास्त्री टॉमस यंग ने स्रोतों S1 तथा S2 से उत्सर्जित होने वाली तरंगों की कलाओं को नियंत्रित करने के लिए एक उत्तम तकनीक उपयोग की| उन्होंने एक अपारदर्शी परदे पर दो सूचिछिद्र S1 तथा S2 (एक-दूसरे को बहुत निकट) बनाए [चित्र 10.12(a)]| इन्हें एक अन्य सूचिछिद्र से प्रदीप्त किया गया जिसे एक दीप्त स्रोत से प्रकाशित किया गया था| प्रकाश तरंगें S से निकलकर S1 तथा S2 पर गिरती हैं| S1 तथा S2 दो कला-संबद्ध स्रोतों की भाँति कार्य करते हैं क्योंकि S1 तथा S2 से निकलने वाली प्रकाश तरंगें एक ही मूल स्रोत से व्युत्पन्न होती हैं तथा स्रोत S में अचानक कोई भी कला परिवर्तन S1 तथा S2 से आने वाले प्रकाश में ठीक उसी प्रकार का कला परिवर्तन करेगा| इस प्रकार दोनों स्रोत S1 तथा S2 समान कला में बँध जाएँगे अर्थात वे हमारे जल तरंगों के उदाहरण में [चित्र 10.8(a)] दो कंपित सुइयों की भाँति कला-संबद्ध होंगे|

इस प्रकार S1 तथा S2 से उत्सर्जित होने वाली गोलीय तरंगें चित्र 10.12(b) की भाँति परदे GG′ पर व्यतिकरण फ्रिंजें उत्पन्न करेंगी| अधिकतम तथा न्यूनतम तीव्रता की स्थितियों की गणना अनुच्छेद 10.4 में दिए गए विश्लेषण का उपयोग करके की जा सकती है, जहाँ पर हमने रेखा GG′ [चित्र 10.12(b)] पर एक यथेच्छ बिंदु P लिया जो अधिकतम तीव्रता के संगत है| इस अवस्था में

S2P – S1P = nλ; n = 0, 1, 2 ... (10.15)

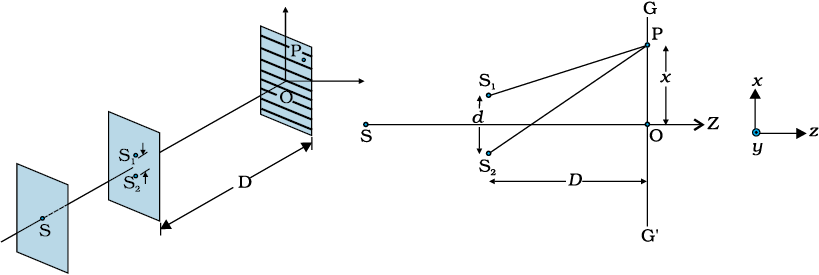
चित्र 10.12 व्यतिकरण पैटर्न उत्पन्न करने के लिए टॉमस यंग की व्यवस्था|

अब

(S2P)2 – (S1P)2 = 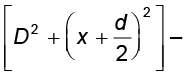= 2xd

जहाँ पर S1S2 = d तथा OP = x | अतः,

(a) (b)

S2P – S1P = 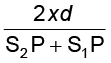(10.16)

यदि x, d<<D तो यदि S2P + S1P (जो हर में है) को 2D से प्रतिस्थापित कर दें तो केवल नगण्य त्रुटि ही सन्निविष्ट होगी| उदाहरण के लिए d = 0.1 cm, D = 100 cm, OP = 1 cm के लिए (जो प्रकाश तरंगों का उपयोग करके व्यतिकरण प्रयोग के लिए विशिष्ट मानों के संगत हैं) हमें प्राप्त होगा

S2P + S1P = [(100)2 + (1.05)2]½ + [(100)2 + (0.95)2]½

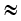200.01 cm

इस प्रकार यदि हम S2P + S1P को 2 D से प्रतिस्थापित कर दें तो लगभग 0.005% त्रुटि आवेष्टित होगी| इस सन्निकटन से समीकरण (10.16) होगी,

S2P – S1P ≈ 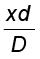(10.17)

इस प्रकार समीकरण 10.10 के अनुसार हमें संपोषी व्यतिकरण द्वारा दीप्त क्षेत्र प्राप्त होंगे जब 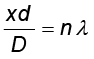[समीकरण (10.15)], अर्थात

x = xn = 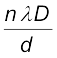; n = 0, 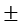1, 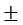2, ... (10.18)

होगा| दूसरी ओर हमें विनाशी व्यतिकरण द्वारा अदीप्त क्षेत्र प्राप्त होंगे जब अर्थात

x = xn = (n+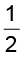) 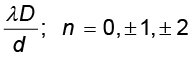(10.19)

के निकट अदीप्त क्षेत्र प्राप्त होंगे|

इस प्रकार चित्र 10.13 की भाँति परदे पर अदीप्त तथा दीप्त बैंड दिखलाई देंगे| एेसे बैंडों को फ्रिंज कहते हैं| समीकरण (10.18) तथा (10.19) दर्शाती है कि काले तथा दीप्त फ्रिंज समान दूरी पर हैं तथा दो क्रमागत अदीप्त तथा दीप्त फ्रिंजों के बीच की दूरी होगी

β = xn+1 –xn

अथवा β = 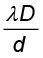(10.20)

टॉमस यंग (1773-1829)

अंग्रेज़ भौतिकविद, कायचिकित्सक एवं मिस्र विशेषज्ञ| यंग ने बहुत तरह की वैज्ञानिक समस्याओं पर कार्य किया, जिनमें एक ओर आँख की संरचना और दृष्टि प्रक्रिया तो दूसरी ओर रोसेटा मणि का रहस्य भेदन शामिल है| उन्होंने प्रकाश के तरंग सिद्धांत को पुनर्जीवित किया और समझाया कि व्यतिकरण, प्रकाश के तरंग गुण का प्रमाण प्रस्तुत करता है|

यह फ्रिंज-चौड़ाई का व्यंजक है| स्पष्टतया मध्य बिंदु O (चित्र 10.12) दीप्त होगा क्योंकि S1O = S2O तथा यह n = 0 के संगत होगा (समीकरण 10.18)| यदि हम कागज़ के तल के लंबवत तथा O से गुजरने वाली रेखा पर विचार करें (अर्थात, y-अक्ष के अनुदिश) तो इस रेखा पर सभी बिंदु S1 तथा S2 से समान दूरी पर होंगे और हमें दीप्त मध्य फ्रिंज मिलेगा, जो चित्र 10.13 में दर्शाए अनुसार एक सरल रेखा है| परदे पर व्यतिकरण पैटर्न की आकृति ज्ञात करने के लिए हम देखेंगे कि एक विशेष फ्रिंज S2P–S1P के नियत मान के बिंदु पथ के संगत है| जब भी यह नियतांक λ का समाकल गुणक है, फ्रिंज दीप्त होगा तथा जब यह λ/2 का विषम समाकल गुणक है, फ्रिंज अदीप्त होगा| अब x-y तल में स्थित बिंदु P का बिंदु पथ इस प्रकार होगा कि S2P – S1P (= ∆) एक नियतांक होने के कारण एक अति परवलयकार होगा| इस प्रकार फ्रिंज पैटर्न सुनिश्चित रूप से अतिपरवलय है; तथापि यदि दूरी D फ्रिंज चौड़ाई की अपेक्षा बहुत अधिक है, तो फ्रिंजें काफ़ी हद तक सीधी रेखाएँ होंगी, जैसा कि चित्र 10.13(b) में दर्शाया गया है|

चित्र 10.12(b) में दर्शाए द्वि-झिरी प्रयोग में हमने स्रोत छिद्र S को दोनों झिरियों के लंबअर्धक पर रखा है, जिसे SO रेखा से प्रदर्शित किया गया है| यदि स्रोत S लंबअर्धक से थोड़ा दूर हो तो क्या होगा? मान लीजिए स्रोत S को किसी नयी स्थिति S′ तक खिसका दिया गया है और Q, S1 तथा S2 का मध्यबिंदु है| यदि कोण S′ QS का मान φ है तब केंद्रीय दीप्त फ्रिंज दूसरी दिशा में –φ कोण पर मिलेगा| इस प्रकार यदि स्रोत S लंबअर्धक पर है, तब केंद्रीय फ्रिंज बिंदु O पर होगा जो कि लंबअर्धक पर होगा| यदि स्रोत S किसी नए बिंदु S′ पर कोण φ से खिसका दिया गया है, तब केंद्रीय फ्रिंज कोण –φ पर स्थित O′ बिंदु पर दिखलाई देगा, जिसका अर्थ है कि यह लंबअर्धक से दूसरी ओर इतने ही कोण से खिसक जाएगा| इसका अर्थ यह भी है कि स्रोत S′ मध्य बिंदु Q तथा केंद्रीय फ्रिंज का बिंदु O′ एक सरल रेखा में हैं|

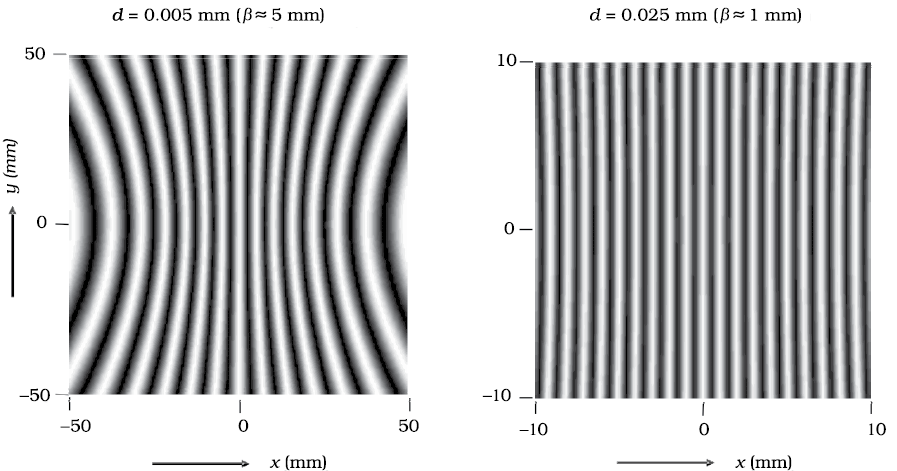
चित्र 10.13 दो स्रोतों S1 तथा S2 द्वारा GG′ परदे पर (देखिए चित्र 10.12 ) उत्पन्न हुआ कंप्यूटर द्वारा बनाया गया फ्रिंज पैटर्न;

(a) तथा (b) संगत हैं क्रमशः d = 0.005 mm तथा 0.025 mm के लिए (दोनों चित्रों में D = 5 cm तथा λ = 5 × 10–5 cm) (‘अॉपटिक्स’ ए. घटक, टाटा मैक्ग्रा हिल पब्लिशिंग कं.लि., नयी दिल्ली, 2000 से लिया गया|)

इस अनुच्छेद को हम डेनिस गेबर* के नोबेल भाषण के उद्धरण से समाप्त करेंगे|

प्रकाश की तरंग प्रकृति को टॉमस यंग ने सन् 1801 में पहली बार एक सरल तथा आश्चर्यजनक प्रयोग द्वारा युक्तियुक्त तरीके से प्रदर्शित किया| उन्होंने सूर्य के प्रकाश की एक किरण को अँधेरे कमरे में आने दिया, उसके सामने दो बारीक सूचिछिद्र बनाकर एक काला परदा रखा तथा उसके आगे कुछ दूरी पर एक सफ़ेद परदा रखा| उन्होंने एक दीप्त रेखा के दोनों ओर दो काली-सी रेखाएँ देखीं जिसने उन्हें इस प्रयोग को दोहराने के लिए पर्याप्त प्रोत्साहन दिया| लेकिन इस बार उन्होंने दीप्त पीला सोडियम प्रकाश उत्पन्न करने के लिए प्रकाश स्रोत की तरह एक स्प्रिट लैंप का उपयोग किया, जिसमें थोड़ा-सा नमक डाल रखा था| इस बार उन्हें समान दूरी पर स्थित अनेक काली रेखाएँ दिखलाई दीं| यह पहला स्पष्ट प्रमाण था कि प्रकाश से प्रकाश को मिलाने पर अँधेरा पैदा हो सकता है| इस परिघटना को व्यतिकरण कहा जाता है| टॉमस यंग की एेसी ही अपेक्षा थी क्योंकि वह प्रकाश के तरंग सिद्धांत में विश्वास करते थे|

यहाँ यह उल्लेख करना आवश्यक है कि यद्यपि S1 तथा S2 बिंदु स्रोत हैं फिर भी फ्रिंज सीधी रेखाएँ हैं| यदि बिंदु स्रोतों के स्थान पर हमारे पास झिरियाँ होंगी (चित्र 10.14), तो बिंदुओं का प्रत्येक युग्म सीधी रेखा फ्रिंज उत्पन्न करेगा, जिसके परिणामस्वरूप बढ़ी हुई तीव्रता के सीधी रेखा फ्रिंज प्राप्त होंगे|

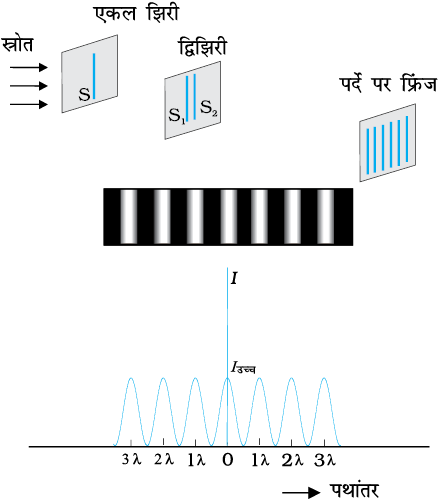
चित्र 10.14 यंग के द्विझिरी प्रयोग में तीव्रता वितरण का फ़ोटोग्राफ़ तथा ग्राफ़

उदाहरण 10.3 दो झिरियाँ 1 मिलीमीटर दूर बनाई गई हैं और परदे को एक मीटर दूर रखा गया है| फ्रिंज अंतराल कितना होगा जब 500 nm तरंगदैर्घ्य का नीला-हरा प्रकाश प्रयोग में लाया जाता है?

हल फ्रिंज अंतराल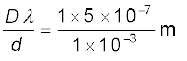

= 5 × 10–4 m = 0.5 mm

उदाहरण 10.4 निम्नलिखित प्रचालनों में प्रत्येक के कारण यंग के द्विझिरी प्रयोग के व्यतिकरण पर क्या प्रभाव पड़ेगा?

(a) झिरियों के समतल से परदे को दूर कर देने पर;

(b) (एकवर्णी) स्रोत को दूसरे कम तरंगदैर्घ्य वाले (एकवर्णी) स्रोत से प्रतिस्थापन करने पर;

(d) स्रोत झिरी को द्विझिरी के समतल के समीप लाने पर;

(e) स्रोत झिरी की चौड़ाई बढ़ने पर;

(f) एकवर्णी प्रकाश स्रोत को श्वेत प्रकाश स्रोत से प्रतिस्थापित करने पर;

(प्रत्येक प्रचालन में उल्लेखित प्राचल (पैरामीटर) के अतिरिक्त सभी प्राचल अपरिवर्तनीय हैं|)

हल

(a) फ्रिंजों का कोणीय पार्थक्य अचर रहता है (= λ/d)| फ्रिंजों का वास्तविक पार्थक्य दोनों झिरियों के समतल से परदे की दूरी के समानुपात में बढ़ता है|

(b) फ्रिंजों का पार्थक्य (तथा कोणीय पार्थक्य भी) घटता है| तथापि निम्न (d) खंड में उल्लेखित शर्त देखें|

(d) मान लीजिए s स्रोत का साइज़ है तथा S दोनों झिरियों के समतल से इसकी दूरी है| व्यतिकरण फ्रिंजों को देखने के लिए, निम्न शर्त पूरी होनी चाहिए; s/S < λ/d अन्यथा, स्रोत के विभिन्न भागों द्वारा उत्पन्न व्यतिकरण पैटर्न अतिव्याप्त(overlap) करेंगे तथा फ्रिंजें दिखलाई नहीं देंगी| इस प्रकार जब S घटता है (अर्थात स्रोत झिरी पास लाई जाती है), व्यतिकरण पैटर्न कम और कम स्पष्ट होता जाता है तथा जब स्रोत अत्यंत निकट आ जाता है, इस शर्त के पूरा होने के लिए, फ्रिंजें गायब हो जाती हैं| जब तक एेसा होता है, फ्रिंज अंतराल स्थिर रहता है|

(e) (d) की भाँति| जैसे-जैसे स्रोत झिरी की चौड़ाई बढ़ती है, फ्रिंज पैटर्न कम तथा कम स्पष्ट होता जाता है| जब स्रोत झिरी इतनी चौड़ी हो जाती है कि शर्त s/S ≤ λ/d पूरी नहीं होती, व्यतिकरण पैटर्न गायब हो जाता है|

(f) श्वेत प्रकाश के विभिन्न घटक रंगों के कारण व्यतिकरण पैटर्न का अतिव्यापन होता है (कला-असंबद्ध रूप से)| विभिन्न रंगों के लिए केंद्रीय दीप्ति फ्रिंजें एक ही स्थिति में होते हैं| अतः केंद्रीय फ्रिंज श्वेत होता है| बिंदु P के लिए
S2P–S1P=λb/2, [जहाँ λb (~4000A0) नीले वर्ग के लिए तरंगदैर्घ्य है, नीला रंग अनुपस्थित होगा तथा फ्रिंज का रंग लाल प्रतीत होगा| इससे थोड़ा दूर, S2Q – S1Q = λb = λr/2 [जहाँ λr (8000A0] लालवर्ण का तरंगदैर्घ्य है], फ्रिंज मुख्यतः नीली प्रतीत होगी| केंद्रीय श्वेत फ्रिंज के किसी भी ओर का सबसे समीप का फ्रिंजें लाल प्रतीत होती हैं तथा सबसे दूर का फ्रिंजें नीली प्रतीत होती हैं| कुछ फ्रिंजों के पश्चात कोई स्पष्ट फ्रिंज पैटर्न दिखलाई नहीं देता|

10.6 विवर्तन

यदि हम किसी अपारदर्शी वस्तु के द्वारा बनने वाली छाया को ध्यानपूर्वक देखें तो हम पाएँगे कि ज्यामितीय छाया के क्षेत्र के समीप व्यतिकरण के समान बारी-बारी से उदीप्त तथा दीप्त क्षेत्र आते हैं| एेसा विवर्तन की परिघटना के कारण होता है| विवर्तन एक सामान्य अभिलक्षण है जो सभी प्रकार की तरंगों द्वारा प्रदर्शित किया जाता है, चाहे ये ध्वनि तरंगें हों, प्रकाश तरंगें हों, जल तरंगें हों अथवा द्रव्य तरंगें हों| क्योंकि अधिकांश अवरोधकों के विस्तार से प्रकाश की तरंगदैर्घ्य अत्यंत छोटी है इसीलिए हमें दैनिक जीवन के प्रेक्षणों में विवर्तन के प्रभावों का सामना नहीं करना पड़ता| तथापि, हमारी आँख या प्रकाशिक यंत्रों जैसे दूरदर्शकों अथवा सूक्ष्मदर्शियों का निश्चित वियोजन विवर्तन की परिघटना के कारण सीमित रहता है| वास्तव में जब हम किसी CD को देखते हैं तो उसमें रंग विवर्तन प्रभाव के कारण ही दिखलाई देते हैं| अब हम विवर्तन की परिघटना पर चर्चा करेंगे|

10.6.1 एकल झिरी

यंग के प्रयोग के विवेचन में, हमने कहा है कि एक संकीर्ण एकल झिरी नए स्रोत की तरह कार्य करती है, जहाँ से प्रकाश विस्तारित होता है| यंग के पहले भी, प्रारंभिक प्रयोगकर्ताओं जिनमें न्यूटन भी शामिल थे, के ध्यान में यह आ चुका था कि प्रकाश संकीर्ण छिद्रों तथा झिरियों से विस्तारित होता है| यह कोने से मुड़कर उस क्षेत्र में प्रवेश करता हुआ प्रतीत होता है जहाँ हम छाया की अपेक्षा करते हैं| इन प्रभावों को जिन्हें विवर्तन कहते हैं, केवल तरंग धारणा के उपयोग से ही उचित रूप से समझ सकते हैं| आखिर, आपको कोने के पीछे से किसी को बात करते हुए उसकी ध्वनि तरंगों को सुनकर शायद ही आश्चर्य होता है|

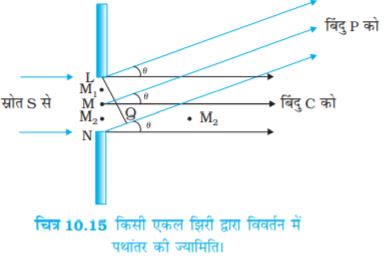
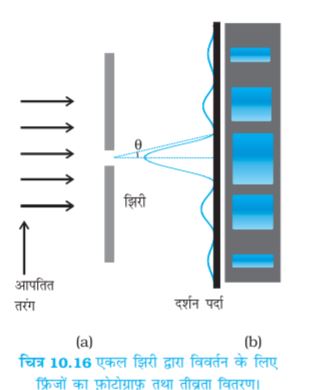
जब यंग के प्रयोग की एकवर्णी स्रोत से प्रकाशित द्विझिरी को एक संकीर्ण एकल झिरी द्वारा प्रतिस्थापित किया जाता है तो एक ब्रॉड (चौड़ा) पैटर्न दिखाई पड़ता है जिसके मध्य में दीप्त क्षेत्र होता है| इसके दोनों ओर क्रमागत दीप्त एवं अदीप्त क्षेत्र होते हैं जिनकी तीव्रता केंद्र से दूर होने पर कम होती जाती है (चित्र 10.16)| इसको समझने के लिए चित्र 10.15 देखिए, जिसमें a चौड़ाई की एकल झिरी LN पर अभिलंबवत पड़ने वाले समांतर किरण पुंज को दर्शाया गया है| विवर्तित प्रकाश आगे रखे एक परदे पर आपतित होता है| झिरी का मध्य बिंदु M है|

बिंदु M से गुज़रने वाली और झिरी के तल के अभिलंबवत सरल रेखा परदे को बिंदु C पर मिलती है| हमें परदे के किसी बिंदु P पर तीव्रता ज्ञात करनी है| जैसा पहले चर्चा कर चुके हैं, P को विभिन्न बिंदुओं L, M, N आदि से जोड़ने वाली विभिन्न सरल रेखाएँ परस्पर समांतर एवं अभिलंब MC से कोण θ बनाती हुई मानी जा सकती हैं [चित्र 10.15]|

मूल धारणा यह है कि झिरी को बहुत से छोटे भागों में विभाजित किया जाए और बिंदु P पर उनके योगदानों को उचित कलांतर के साथ जोड़ा जाए| हम झिरी पर प्राप्त तरंगाग्र के विभिन्न भागों को द्वितीयक स्रोतों की तरह व्यवहार में लाते हैं| क्योंकि, आपाती तरंगाग्र झिरी के तल में समांतर है, तथा ये स्रोत एक ही कला में होते हैं|

झिरी के दो सिरों के बीच के पथांतर (NP – LP) की गणना ठीक उसी प्रकार की जा सकती है जैसे कि टॉमस यंग के प्रयोग में की थी| चित्र 10.15 से,

NP – LP = NQ

= a sin θ

≈ aθ (10.21)

(छोटे कोणों के लिए)

इसी प्रकार, यदि झिरी के तल में दो बिंदुओं M1 एवं M2 के बीच दूरी y हो तो पथांतर M2P – M1P ≈ yθ | अब, हमें स्रोतों की बड़ी संख्या से प्राप्त होने वाले समान, कला-संबद्ध योगदानों को जोड़ना है जिनमें से प्रत्येक भिन्न कला संपन्न होता है| यह गणना फ्रेनेल द्वारा समाकलन के उपयोग द्वारा की गई थी तथा हम यहाँ इस पर विचार नहीं करेंगे| विवर्तन पैटर्न के मुख्य अभिलक्षण साधारण तर्कों द्वारा समझे जा सकते हैं|

परदे के केंद्रीय बिंदु C पर, कोण θ शून्य है| सभी पथांतर शून्य हैं| अतः झिरी के सभी भागों का योगदान समकला में है| इससे बिंदु C पर उच्चतम तीव्रता मिलती है| चित्र 10.15 के प्रायोगिक प्रेक्षण दर्शाते हैं कि तीव्रता का केंद्रीय उच्चिष्ठ θ = 0 पर है तथा दूसरे द्वितीयक उच्चिष्ठ θ 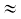(n+1/2)
λ/a पर हैं तथा निम्निष्ठ (शून्य तीव्रता) θ 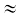nλ/a, n = ±1, ±2, ±3, .... पर हैं| यह देखना आसान है कि कोणों के इन मानों के लिए निम्निष्ठ क्यों प्राप्त होते हैं| पहले कोण θ पर विचार करें, जहाँ पथांतर aθ, λ है तब,

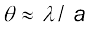(10.22)

अब, झिरी को दो बराबर भागों LM तथा MN में बाँटें जिनमें प्रत्येक का आकार a/2 है| भाग LM में प्रत्येक बिंदु M1 के लिए भाग MN में बिंदु M2 इस प्रकार है कि M1M2 = a/2 | बिंदु P पर M1 तथा M2 के बीच पथांतर चुने हुए कोण θ के लिए M2P – M1P = θa/2 = λ/2| इसका अर्थ यह है कि M1 तथा M2 के योगदान 180º से विपरीत कला में हैं तथा θ = λ/a दिशा में रद्द हो जाते हैं| इसलिए झिरी के दो अर्द्धभागों LM तथा MN के योगदान एक-दूसरे को रद्द कर देते हैं| समीकरण (10.22) वह कोण बताती है जिस पर तीव्रता शून्य हो जाती है| इसी प्रकार यह दर्शाया जा सकता है कि θ = nλ/a के लिए तीव्रता शून्य होगी, जहाँ n एक पूर्णांक है (शून्य के अलावा)| ध्यान दें कि झिरी का आकार a घटने से केंद्रीय उच्चिष्ठ का कोणीय साइज़ बढ़ता है|

यह देखना भी आसान है कि θ = (n + 1/2) λ/a पर उच्चिष्ठ क्यों प्राप्त होता है तथा n का मान बढ़ने पर इनकी तीव्रता लगातार कम क्यों होती जाती है| अब एक कोणθ = 3λ/2a पर विचार करें जो दो अदीप्त फ्रिंजों के मध्य में है| झिरी को तीन बराबर भागों में बाँटें| यदि हम प्रथम दो-तिहाई झिरी को लें तो दो सिरों के बीच पथांतर होगा

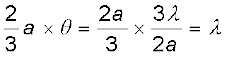(10.23)

इसलिए, प्रथम दो-तिहाई झिरी को दो अर्द्धभागों में विभाजित किया जा सकता है जिनका पथांतर λ/2 होगा| इन दो अर्द्धभागों के योगदान उसी प्रकार रद्द हो जाते हैं जैसे कि पहले वर्णन किया गया है| केवल शेष एक-तिहाई भाग ही दो निम्निष्ठों के मध्य किसी बिंदु पर तीव्रता को योगदान देता है| स्पष्टतः यह केंद्रीय उच्चिष्ठ की अपेक्षा काफ़ी क्षीण होगा (जहाँ पूरी झिरी समकला में योगदान देती है)| इसी प्रकार, यह दिखाया जा सकता है कि (n + 1/2) λ/a जहाँ n = 2, 3, आदि पर उच्चिष्ठ प्राप्त होगा| ये n के बढ़ने के साथ क्षीण होते जाते हैं, क्योंकि झिरी का केवल पाँचवाँ, सातवाँ आदि भाग ही इन स्थितियों में योेगदान देता है| फ़ोटोग्राफ़ तथा इसके संगत तीव्रता पैटर्न चित्र 10.16 में दर्शाए गए हैं|

व्यतिकरण तथा विवर्तन में क्या अंतर है, इस संबंध में इन परिघटनाओं की खोज के समय से ही वैज्ञानिकों में लंबा विचार-विमर्श होता रहा है| इस संबंध में रिचर्ड फ़ाइनमैन* ने अपने प्रसिद्ध फ़ाइनमैन लेक्चर्स अॉन फ़िजिक्स में क्या कहा है, यह जानना दिलचस्प रहेगा|

अभी तक कोई भी व्यतिकरण तथा विवर्तन के बीच अंतर को संतोषप्रद रूप से परिभाषित नहीं कर पाया है| यह केवल उपयोग का प्रश्न है, इन दोनों के बीच कोई सुस्पष्ट तथा महत्वपूर्ण भौतिक अंतर नहीं है| मोटे तौर से हम अधिक से अधिक कह सकते हैं कि जब केवल कुछ स्रोत होते हैं, मान लीजिए दो व्यतिकारी स्रोत, तब प्रायः मिलने वाले परिणाम को व्यतिकरण कहते हैं, लेकिन यदि इनकी संख्या बहुत अधिक हो, एेसा प्रतीत होता है कि विवर्तन शब्द प्रायः उपयोग किया जाता है|

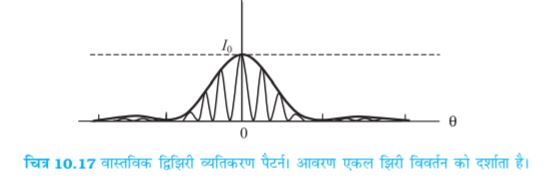
द्विझिरी प्रयोग में, हमें ध्यान देना चाहिए कि परदे पर बनने वाला पैटर्न वास्तव में प्रत्येक झिरी या छिद्र द्वारा अध्यारोपण से बनने वाला एकल झिरी विवर्तन पैटर्न है, तथा द्विझिरी व्यतिकरण पैटर्न है| इसे चित्र 10.17 में दर्शाया गया है| यह एक विस्तृत विवर्तन शीर्ष दर्शाता है जिसमें द्विझिरी व्यतिकरण के कारण अनेक कम चौड़ाई के फ्रिंज दिखलाई देते हैं| विस्तृत विवर्तन शीर्ष में विद्यमान व्यतिकरण फ्रिंजों की संख्या अनुपात d/a अर्थात दो झिरियों के बीच की दूरी तथा झिरी की चौड़ाई के अनुपात पर निर्भर है| a के बहुत छोटे बनने की सीमा में, निवर्तन पैटर्न बहुत समतल बनेगा तथा हमें द्विझिरी व्यतिकरण पैटर्न दिखाई देगा [देखिए चित्र 10.13 (b)]

उदाहरण 10.5 उदाहरण 10.3 में, प्रत्येक झिरी की चौड़ाई कितनी होनी चाहिए जिससे कि एकल झिरी पैटर्न के केंद्रीय उच्चिष्ठ के भीतर द्विझिरी पैटर्न के 10 उच्चिष्ठ प्राप्त हो सकें?

हल हम चाहते हैं

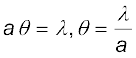
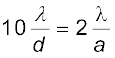
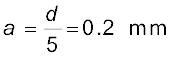
ध्यान दें कि प्रकाश की तरंगदैर्घ्य तथा परदे की दूरी, झिरी की चौड़ाई a के परिकलन में शामिल नहीं होती|

चित्र 10.12 के द्विझिरी व्यतिकरण प्रयोग में यदि हम एक झिरी को बंद कर दें तो क्या होगा? आप देखेंगे कि अब यह एक एकल झिरी की भाँति कार्य करता है| परंतु आपको पैटर्न के कुछ खिसकने पर ध्यान देना होगा| अब हमारे पास S पर एक स्रोत है तथा केवल एक छिद्र (या झिरी) S1 या S2 | यह परदे पर एकल झिरी विवर्तन पैटर्न उत्पन्न करेगी| केंद्रीय दीप्त फ्रिंज का केंद्र उस बिंदु पर दिखलाई देगा जो वस्तु स्थिति के अनुसार सरल रेखा SS1 या SS2 पर स्थित होगा|

अब हम व्यतिकरण पैटर्न तथा संबद्धतया प्रदीप्त एकल झिरी के पैटर्न (जिसे सामान्यतया एकल झिरी विवर्तन पैटर्न कहते हैं) की समानता तथा विषमता का वर्णन करेंगे|

(i) व्यतिकरण पैटर्न में समान अंतराल पर दीप्त तथा अदीप्त बैंड होते हैं| विवर्तन पैटर्न में एक केंद्रीय दीप्त उच्चिष्ठ होता है जो दूसरे उच्चिष्ठों से दो गुना चौड़ा है| केंद्र के दोनों ओर दूर आनुक्रमिक उच्चिष्ठों पर तीव्रता कम होती जाती है|

(ii) हम व्यतिकरण पैटर्न का परिकलन दो संकीर्ण झिरियों से उद्गमित दो तरंगों के अध्यारोपण द्वारा करते हैं| विवर्तन पैटर्न एक एकल झिरी के प्रत्येक बिंदु से उद्गमित सतत तरंग परिवार के अध्यारोपण से प्राप्त होता है|

(iii) चौड़ाई a की किसी एकल झिरी के लिए, व्यतिकरण पैटर्न का पहला शून्य कोण λ/a पर स्थित होता है| इसी कोण λ/a पर हमें दो संकीर्ण झिरियों जिनके बीच की दूरी a है, के लिए उच्चिष्ठ (शून्य नहीं) मिलता है|

हमें यह समझ लेना चाहिए कि अच्छा व्यतिकरण तथा विवर्तन पैटर्न देख पाने के लिए d तथा a दोनों ही काफ़ी छोटे होने चाहिए| उदाहरण के लिए, दो झिरियों के बीच प्राथक्य लगभग एक मिलीमीटर की कोटि का होना चाहिए| प्रत्येक झिरी की चौड़ाई a और भी छोटी होनी चाहिए, लगभग 0.1 या 0.2 mm की कोटि के बराबर|

* रिचर्ड फ़ाइनमैन को 1965 का भौतिकी का नोबेल पुरस्कार मिला जो उनके क्वांटम वैद्युतगतिकी के मौलिक कार्य पर दिया गया|

यंग के प्रयोग तथा एकल झिरी विवर्तन के हमारे विवेचन में, हमने यह माना है कि परदा जिस पर फ्रिंजें बनती हैं, अधिक दूरी पर है| झिरी से परदे तक के दो अथवा अधिक पथों को समांतर माना गया था| यही स्थिति तब भी पाई जाती है जब हम एक अभिसारी लेंस को झिरियों के बाद रखते हैं तथा परदे को लेंस के फ़ोकस पर रखते हैं| झिरी से समांतर पथ परदे पर एक बिंदु पर मिलते हैं| ध्यान दें कि किसी समांतर किरण-पुंज में लेंस कोई अतिरिक्त पथांतर उत्पन्न नहीं करता है| यह व्यवस्था बहुधा उपयोग में लाई जाती है क्योंकि इससे परदे को बहुत दूर रखने की तुलना में अधिक तीव्रता मिलती है| यदि लेंस की फ़ोकस दूरी f है, तब हम सरलता से केंद्रीय दीप्त उच्चिष्ठ का साइज़ ज्ञात कर सकते हैं| कोणों के रूप में, विवर्तन पैटर्न के प्रथम शून्य से केंद्रीय उच्चिष्ठ का अंतराल λ/a है| अतः परदे पर इसका साइज़ f λ/a होगा|

10.6.2 एकल झिरी विवर्तन पैटर्न का अवलोकन

एकल झिरी विवर्तन पैटर्न को स्वयं ही देखना आश्चर्यजनक रूप से सरल है| आवश्यक उपकरण अधिकांश घरों में पाया जा सकता है– दो रेज़र ब्लेड तथा एक पारदर्शक काँच का विद्युत बल्ब (किसी सीधे तंतु वाले बल्ब को वरीयता प्रदान करें)| दोनों ब्लेडों को इस प्रकार पकड़ा जाता है कि उनके किनारे समांतर हों और दोनों के बीच एक संकीर्ण झिरी बने| यह सरलता से अँगूठे तथा उँगलियों के द्वारा भी किया जा सकता है (चित्र 10.18)|

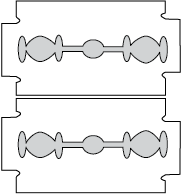
चित्र 10.18 एक एकल झिरी निर्मित करने के लिए दो ब्लेडों को पकड़ना| एक बल्ब तंतु जिसे झिरी में से देखा जाता है, स्पष्ट विवर्तन बैंड दर्शाता है|

झिरी को फ़िलामेंट के समांतर रखिए, ठीक आँख के सामने| यदि आप चश्मा पहनते हैं तो उसका उपयोग करें| झिरी की चौड़ाई तथा किनारों की समांतरता के कुछ समायोजन से दीप्त तथा अदीप्त बैंडों के साथ पैटर्न दिखाई देना चाहिए| क्योंकि सभी बैंडों की स्थिति (केंद्रीय बैंड को छोड़कर) तरंगदैर्घ्य पर निर्भर है, वे कुछ रंग दर्शाएँगी| लाल तथा नीले के लिए फ़िल्टर के उपयोग से फ्रिंजें अधिक स्पष्ट हो जाएँगी| यदि दोनों फ़िल्टर उपलब्ध हों तो नीले की तुलना में लाल रंग की फ्रिंजें अधिक चौड़ी देखी जा सकती हैं|

इस प्रयोग में, तंतु प्रथम स्रोत S की भूमिका निभा रहा है (चित्र 10.15)| नेत्र का लेंस परदे (नेत्र के रेटिना) पर पैटर्न को फ़ोकस करता है|

थोड़े प्रयत्न से, एक ब्लेड की सहायता से एेलुमिनियम की पन्नी में द्विझिरी काटी जा सकती है| बल्ब तंतु को यंग के प्रयोग को दोहराने के लिए पहले की भाँति देखा जा सकता है| दिन के समय में, नेत्र पर एक छोटा कोण बनाने वाला एक दूसरा उपयुक्त दीप्त स्रोत है| यह किसी चमकीले उत्तल पृष्ठ (उदाहरण के लिए एक साइकिल की घंटी) में सूर्य का परावर्तन है| सूर्य-प्रकाश के साथ सीधे ही प्रयोग न करें– यह नेत्र को क्षति पहुँचा सकता है तथा इससे फ्रिंजें भी नहीं मिलेंगी क्योंकि सूर्य (1/2)° का कोण बनाता है|

व्यतिकरण तथा विवर्तन में प्रकाश ऊर्जा का पुनर्वितरण होता है| यदि यह अदीप्त फ्रिंज उत्पन्न करते समय एक क्षेत्र में घटती है तो दीप्त फ्रिंज उत्पन्न करते समय दूसरे क्षेत्र में बढ़ती है| ऊर्जा में कोई लाभ अथवा हानि नहीं होती जो ऊर्जा संरक्षण के सिद्धांत के अनुकूल है|

10.6.3 प्रकाशिक यंत्रों की विभेदन क्षमता

अध्याय 9 में हमने दूरदर्शकों के बारे में चर्चा की थी| दूरदर्शी का कोणीय विभेदन इसके अभिदृश्यक से निर्धारित होता है| अभिदृश्यक द्वारा बनाए गए प्रतिबिंब में जो तारे विभेदित नहीं हो पाते वे नेत्रिका द्वारा उत्पन्न आवर्धन द्वारा भी विभेदित नहीं हो सकते| नेत्रिका का प्रारंभिक उद्देश्य, अभिदृश्यक द्वारा उत्पन्न प्रतिबिंब को और अधिक आवर्धित करना है|

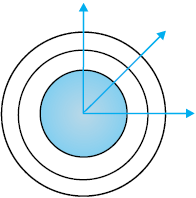
एक उत्तल लेंस पर गिरने वाले एक समांतर किरण-पुंज पर विचार करें| यदि लेंस विपथन के लिए पूर्ण रूप से संशोधित है तब ज्यामितीय प्रकाशिकी के अनुसार किरण-पुंज एक बिंदु पर फ़ोकसित होगा| तथापि, विवर्तन के कारण, किरण-पुंज एक बिंदु पर फ़ोकसित होने की बजाय एक परिमित क्षेत्रफल में फ़ोकसित होगा| इस दशा में विवर्तन के प्रभावों को एक समतल तरंग को उत्तल लेंस से पहले रखे वृत्ताकार द्वारक पर आपतित कराकर (चित्र 10.19 देखें) ज्ञात कर सकते हैं| संगत विवर्तन पैटर्न का विश्लेषण पर्याप्त पेचीदा है; तथापि, सिद्धांततः यह एकल झिरी विवर्तन पैटर्न के विश्लेषण करने के समान है| विवर्तन के प्रभावों को ध्यान में रखते हुए फ़ोकस समतल पर बनने वाले पैटर्न में एक केंद्रीय दीप्त क्षेत्र होगा, जो चारों ओर से अदीप्त तथा दीप्त संकेंद्रित वलयों से घिरा होगा (चित्र 10.19)| विस्तृत विश्लेषण से ज्ञात होता है कि केंद्रीय दीप्त क्षेत्र की त्रिज्या लगभग

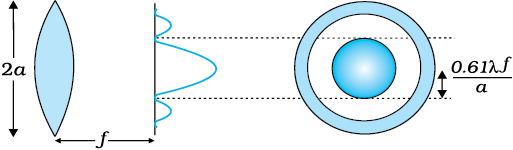
चित्र 10.19 उत्तल लेंस पर आपतित प्रकाश का एक समांतर किरण-पुंज| विवर्तन प्रभावों के कारण, किरण-पुंज लगभग ≈ 0.61 λf/a की त्रिज्या के धब्बे के रूप में फ़ोकसित हो जाती है|

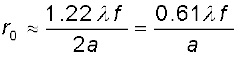(10.24)

होती है| जहाँ पर f लेंस की फ़ोकस दूरी तथा 2a, वृत्ताकार द्वारक के व्यास अथवा लेंस के व्यास में जो भी कम हो वही है|

उदाहरण के लिए, यदि

λ ≈ 0.5 µm, f ≈ 20 cm तथा a ≈ 5 cm

तो हमें प्राप्त होगा

r0 ≈ 1.2 µm

यद्यपि धब्बे का साइज़ बहुत छोटा है फिर भी यह प्रकाशिक यंत्रों जैसे दूरदर्शक या सूक्ष्मदर्शी की विभेदन सीमा ज्ञात करने में एक महत्वपूर्ण भूमिका निभाता है| दो तारों को मात्र विभेदित करने के लिए

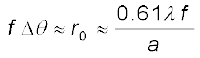
इससे ज्ञात होता है

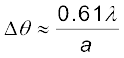(10.25)

अतः यदि अभिदृश्यक का व्यास अधिक है तो ∆θ छोटा होगा| इससे पता चलता है कि यदि a का मान अधिक है तो दूरदर्शी की विभेदन क्षमता अधिक होगी| यही कारण है कि अच्छे विभेदन के लिए दूरदर्शक के अभिदृश्यक का व्यास अधिक होना चाहिए|

उदाहरण 10.6 मान लीजिए किसी तारे से 6000Å तरंगदैर्घ्य का प्रकाश आ रहा है| किसी दूरदर्शी के विभेदन की सीमा क्या होगी यदि उसके अभिदृश्यक का व्यास 100 इंच है?

हल एक 100 इंच के दूरदर्शक का अर्थ है कि 2a = 100 इंच = 254 cm अतः यदि

λ ≈ 6000Å = 6×10–5 cm

तब

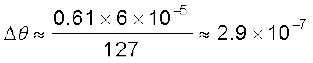रेडियन

चित्र 10.20 एक सूक्ष्मदर्शी के अभिदृश्यक लेंस के द्वारा निर्मित वास्तविक प्रतिबिंब|

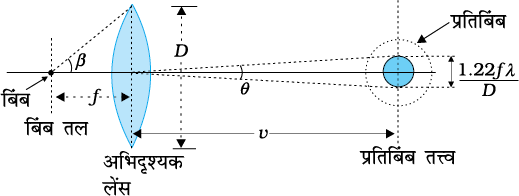
हम एक सूक्ष्मदर्शी के अभिदृश्यक लेंस (objective lens) के लिए समान तर्क का उपयोग कर सकते हैं| इस स्थिति में बिंब (वस्तु) को f से थोड़ा अधिक दूर रखा गया है, जिससे कि दूरी v पर वास्तविक प्रतिबिंब बनता है (चित्र 10.20)| आवर्धन (प्रतिबिंब आकार तथा बिंब आकार का अनुपात) m v/f से ज्ञात किया जाता है| चित्र 10.20 से

D/f ≈ 2 tan β (10.26)

जहाँ 2β सूक्ष्मदर्शी के फ़ोकस पर अभिदृश्यक लेंस के व्यास द्वारा बनाया गया कोण है|

जब किसी सूक्ष्मदर्शीय नमूने में दो बिंदुओं की दूरी, प्रकाश के तरंगदैर्घ्य λ से तुलनीय हो तो विवर्तन प्रभाव महत्वपूर्ण हो जाते हैं| एक बिंदु बिंब का प्रतिबिंब पुनः एक विवर्तन पैटर्न होगा, प्रतिबिंब के समतल में जिसका साइज़

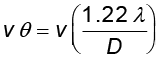(10.27)

होगा| दो बिंब जिनके प्रतिबिंब इस दूरी से कम पर होंगे, विभेदित नहीं होंगे, वे एक ही दिखाई देंगे| बिंब तल में संगत न्यूनतम दूरी, dन्यून होगी

dन्यून =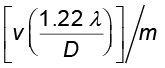

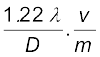
या, क्योंकि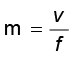

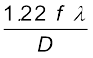= (10.28)

अब समीकरणों (10.26) तथा (10.28) के संयोजन से हमें प्राप्त होगा

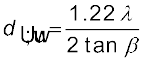
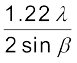~ (10.29)

यदि बिंब तथा अभिदृश्यक लेंस के बीच वायु न होकर अपवर्तनांक n का एक माध्यम है तो समीकरण (10.29) संशोधित हो जाती है

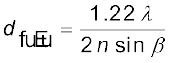(10.30)

गुणनफल n sinβ को संख्यात्मक द्वारक कहते हैं तथा यह कभी-कभी अभिदृश्यक पर अंकित होता है|

सूक्ष्मदर्शी की विभेदन क्षमता सुस्पष्ट दिखने वाले दो बिंदुओं के बीच की न्यूनतम दूरी के व्युत्क्रम से व्यक्त की जाती है| समीकरण (10.30) से यह देखा जा सकता है कि एक उपयुक्त उच्चतर अपवर्तनांक वाले माध्यम के प्रयोग से विभेदन क्षमता को बढ़ाया जा सकता है| प्रायः एक तेल जिसका अपवर्तनांक लेंस के काँच के अपवर्तनांक के समीप है, का उपयोग किया जाता है| इस व्यवस्था को एक तैल निमज्जन अभिदृश्यक कहते हैं| ध्यान दें कि sinβ के मान को एक से अधिक करना संभव नहीं है| इस प्रकार, हम यह देखते हैं कि एक सूक्ष्मदर्शी की विभेदन क्षमता मूलतः उपयोग में लाए गए प्रकाश की तरंगदैर्घ्य से निर्धारित होती है|

विभेदन तथा आवर्धन के बीच भ्रांति होने की काफ़ी संभावना है, और इसी प्रकार इन प्राचलों (parameters) के व्यवहार में दूरदर्शी तथा सूक्ष्मदर्शी की भूमिका के बीच भी भ्रांति की संभावना है| एक दूरदर्शी, दूर के बिंबों का प्रतिबिंब हमारी आँख के निकट बनाता है| इसलिए जिन बिंबों (objects) का विभेदन बहुत अधिक दूरी पर नहीं किया जा सकता, उन्हें दूरदर्शी द्वारा देखकर विभेदित किया जा सकता है| दूसरी ओर, एक सूक्ष्मदर्शी बिंबों को आवर्धित करता है (जो हमारे समीप होते हैं) तथा उनका बड़ा प्रतिबिंब बनाता है| जब हम किन्हीं दो तारों अथवा किसी दूरस्थ ग्रह के दो उपग्रहों को देख रहे हों या हम किसी जीवित कोशिका के विभिन्न भागों को देख रहे हों, तो हमें यह याद रखना चाहिए कि एक दूरदर्शी विभेदन करता है जबकि एक सूक्ष्मदर्शी आवर्धन करता है|

10.6.4 किरण प्रकाशिकी की वैधता

एक a साइज़ का द्वारक (अर्थात झिरी अथवा छिद्र) किसी समांतर किरण-पुंज द्वारा प्रदीप्त होने पर है, लगभग ≈ λ/a कोण में प्रकाश विवर्तित करता है| यह दीप्त केंद्रीय उच्चिष्ठ का कोणीय साइज़ है| अतः एक दूरी z , चलने में केवल विवर्तन के कारण ही विवर्तित किरण-पुंज एक चौड़ाई zλ/a प्राप्त कर लेगा| यह जानना रोचक होगा कि z के किस मान के लिए विवर्तन द्वारा विस्तारण, द्वारक के साइज़ a के तुल्य होगा| इसके लिए हम zλ/a को लगभग a के बराबर मानते हैं| इससे हमें वह दूरी z प्राप्त होती है जिसके आगे a चौड़ाई की किरण-पुंज का अपसरण सार्थक हो जाता है| इसलिए,

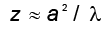(10.31)

हम एक राशि zF जिसे फ्रेनल दूरी कहते हैं, को निम्न समीकरण के द्वारा परिभाषित करते हैं

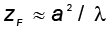
समीकरण (10.31) यह दर्शाती है कि zF से बहुत कम दूरियों के लिए विवर्तन के कारण विस्तारण, किरण-पुंज के साइज़ की तुलना में छोटा है| जब दूरी लगभग zF होती है तब यह तुलनीय हो जाता है| zF से बहुत अधिक दूरियों के लिए, विवर्तन के कारण विस्तारण, किरण-प्रकाशिकी के कारण विस्तारण की तुलना में (अर्थात द्वारक के आकार a की तुलना में) अधिक प्रभावी हो जाता है| समीकरण (10.31) दर्शाती है कि किरण-प्रकाशिकी तरंगदैर्घ्य के शून्य सीमा की ओर अग्रसर होने में वैध है|

उदाहरण 10.7 किस दूरी के लिए किरण-प्रकाशिकी एक अच्छा सन्निकटन है जब द्वारक 3 mm चौड़ा है तथा तरंगदैर्घ्य 500 nm है?

हल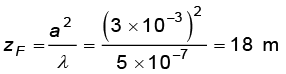

यह उदाहरण प्रदर्शित करता है कि एक लघु द्वारक के लिए भी, विवर्तन विस्तारण कई मीटर लंबी किरणों के लिए उपेक्षित किया जा सकता है| इस प्रकार किरण-प्रकाशिकी कई सामान्य परिस्थितियों में वैध है|

10.7 ध्रुवण

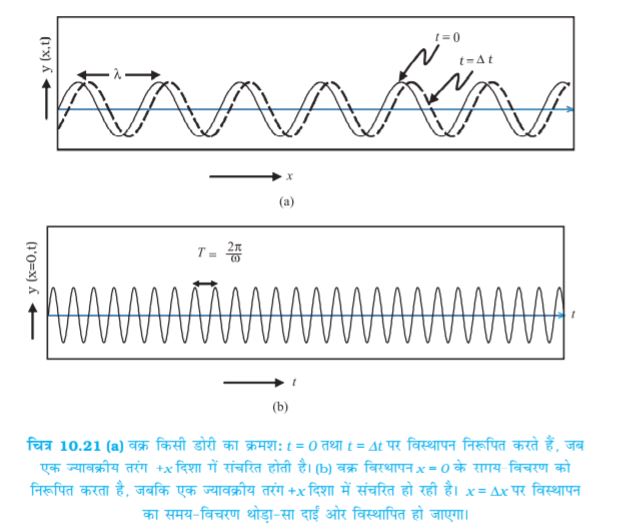
एक लंबी डोरी पर विचार कीजिए जिसे क्षैतिज रखकर पकड़ा गया है और इसका दूसरा सिरा स्थिर माना गया है| यदि हम डोरी के सिरे को ऊपर-नीचे आवर्ती रूप से गति कराएँ तो एक तरंग उत्पन्न कर पाएँगे जो +x दिशा में संचारित होगी (चित्र 10.21)| एेसी तरंग को समीकरण (10.32) द्वारा व्यक्त किया जा सकता है|

y (x,t) = a sin (kx – ωt) (10.32)

जहाँ a तथा ω (= 2πν) क्रमशः तरंग का आयाम तथा कोणीय आवृत्ति निरूपित करते हैं| इसके अतिरिक्त,

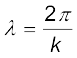(10.33)

तरंग से संबद्ध तरंगदैर्घ्य को निरूपित करता है| इस प्रकार की तरंगों के संचरण की चर्चा हम कक्षा 11 की पाठ्यपुस्तक के अध्याय 15 में कर चुके हैं| क्योंकि विस्थापन (जो y दिशा के अनुदिश है) तरंग संचरण की दिशा के लंबवत है, हमें अनुप्रस्थ तरंगें प्राप्त होती हैं| साथ ही, क्योंकि विस्थापन y दिशा में है, इसीलिए इसे प्रायः y-ध्रुवित तरंग कहा जाता है| क्योंकि डोरी का प्रत्येक बिंदु एक सरल रेखा में गति करता है, तरंग को रैखिकतः ध्रुवित तरंग कहा जाता है| इसके अतिरिक्त, डोरी सदैव x-y तल में ही सीमित रहती है, इसीलिए इसे समतल ध्रुवित तरंग भी कहा जाता है|

इसी प्रकार हम x-z तल में z-ध्रुवित तरंग उत्पन्न करके किसी डोरी के कंपन पर विचार कर सकते हैं, जिसका विस्थापन प्राप्त होगा

z (x,t) = a sin (kx – ωt) (10.34)

यह बतलाना आवश्यक है कि [समीकरणों (10.32) तथा (10.34) से वर्णित] सभी रैखिकतः ध्रुवित तरंगें अनुप्रस्थ तरंगें होती हैं; अर्थात डोरी के प्रत्येक बिंदु का विस्थापन सदैव तरंग संचरण की दिशा के लंबवत होता है| अंततः, यदि डोरी के कंपन के तल को अत्यंत अल्प अंतराल में यादृच्छिकतः बदला जाए तो हमें अध्रुवित तरंग प्राप्त होगी| इस प्रकार एक अध्रुवित तरंग के लिए विस्थापन, समय के साथ, यादृच्छिकतः बदलता रहता है, यद्यपि यह सदैव तरंग संचरण की दिशा के लंबवत रहता है|

प्रकाश की तरंगों की प्रकृति अनुप्रस्थ होती है; अर्थात संचरित हो रही प्रकाश तरंग से संबद्ध विद्युत क्षेत्र सदैव तरंग संचरण की दिशा के लंबवत होता है| इसे एक सरल पोलेरॉइड का उपयोग करके सरलता से प्रदर्शित किया जा सकता है| आपने पतली प्लास्टिक जैसी शीटें देखी होंगी जिन्हें पोलेरॉइड कहते हैं| पोलेरॉइड में अणुओं की एक लंबी शृंखला होती है जो एक विशेष दिशा में पंक्तिबद्ध होते हैं| पंक्तिबद्ध अणुओं की दिशा के अनुदिश विद्युत सदिश (संचरित होती प्रकाश तरंगों से संबद्ध) अवशोषित हो जाता है| इस प्रकार यदि कोई अध्रुवित प्रकाश तरंग एेसे पोलेरॉइड पर आपतित होती तो प्रकाश तरंग रेखीय ध्रुवित हो जाती है, जिसमें विद्युत सदिश पंक्तिबद्ध अणुओं की लंबवत दिशा के अनुदिश दोलन करता है, इस दिशा को पोलेरॉइड की पारित-अक्ष (pass-axis) कहते हैं|

इस प्रकार, जब किसी साधारण स्रोत (जैसे एक सोडियम लैंप) का प्रकाश पोलेरॉइड की किसी शीट P1 से पारित होता है तो यह देखा जाता है कि इसकी तीव्रता आधी हो जाती है| P1 को घुमाने पर पारगत किरण-पुंज पर कोई प्रभाव नहीं पड़ता क्योंकि पारगमित तीव्रता स्थिर रहती है| अब हम एक समरूप पोलेरॉइड P2 को P1 से पहले रखते हैं| अपेक्षानुसार, लैंप से आने वाले प्रकाश की तीव्रता केवल P2 से ही पारित होने में कम हो जाएगी| परंतु अब P1 के घुमाने का P2 से आने वाले प्रकाश पर एक नाटकीय प्रभाव पड़ेगा| एक स्थिति में P2 से पारगमित तीव्रता P1 से पारित होने पर लगभग शून्य हो जाती है| जब इस स्थिति से P1 को 90° पर घुमाते हैं तो यह P2 से आने वाली लगभग पूर्ण तीव्रता को पारगमित कर देता है (चित्र 10.22)|

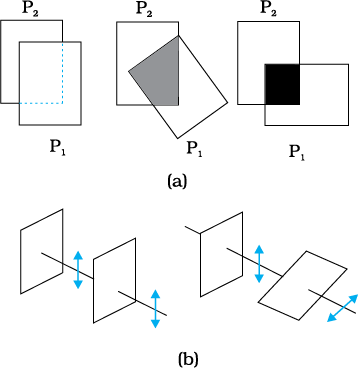
चित्र 10.22 (a) दो पोलेरॉइड P2 तथा P1 से होकर प्रकाश का पारगमन| पारगमित अंश 1 से 0 तक गिरता है, जब उनके बीच का कोण 0° से 90° तक परिवर्तित होता है| ध्यान रखें कि प्रकाश जब एक ही पोलेरॉइड P1 से देखा जाता है तब वह कोण के साथ परिवर्तित नहीं होता| (b) जब प्रकाश दो पोलेरॉइडों से पारित होता है तो विद्युत सदिश का व्यवहार पारगमित ध्रुवण पोलेरॉइड अक्ष के समांतर घटक है| द्विबाणाग्र विद्युत सदिश के दोलन को दर्शाते हैं|

उपरोक्त प्रयोग को यह मानकर आसानी से समझा जा सकता है कि पोलेरॉइड P2 से पारगमित प्रकाश का P2 की पारित अक्ष (pass-axis) के अनुदिश ध्रुवण हो जाता है| यदि P2 की पारित अक्ष, P1 की पारित अक्ष से θ कोण बनाती है, तब जबकि ध्रुवित प्रकाश-पुंज पोलोरॉइड P1 से पारगमित होती है, तो P1 से घटक E cos θ (P1 की पारित अक्ष के अनुदिश) पारित होगा| इस प्रकार जब हम पोलेरॉइड P1 (या पोलेरॉइड P2) को घुमाते हैं तो तीव्रता निम्न प्रकार बदलेगी :

I = I0 cos2θ (10.35)

यहाँ I0, P1 से गुज़रने के पश्चात ध्रुवित प्रकाश की तीव्रता है| इसे मेलस का नियम (Malus' Law) कहते हैं| उपरोक्त विवेचन दर्शाता है कि एक पोलेरॉइड से आने वाले प्रकाश की तीव्रता, आपतित तीव्रता की आधी है| दूसरा पोलेरॉइड रखकर तथा दोनों पोलेरॉइडों की पारित-अक्षों के बीच के कोण को समायोजित करके तीव्रता को आपतित तीव्रता के 50% से शून्य तक नियंत्रित कर सकते हैं|

पोलेरॉइडों को धूप के चश्मों, खिड़की के शीशों आदि में तीव्रता नियंत्रित करने में उपयोग किया जा सकता है| पोलेरॉइडों का उपयोग फ़ोटोग्राफ़ी कैमरों तथा 3D (त्रिआयामी) चलचित्र कैमरों में भी किया जाता है|

उदाहरण 10.8 जब दो क्रॉसित पोलेरॉइडों के बीच में पॉलराइड की एक तीसरी शीट को घुमाया जाता है तो पारगमित प्रकाश की तीव्रता में होने वाले परिवर्तन की विवेचना कीजिए|

हल माना कि प्रथम पोलेराइड P1 से गुज़रने के बाद ध्रुवित प्रकाश की तीव्रता Ia है| तब दूसरे पोलेराइड P2 से गुज़रने के बाद प्रकाश की तीव्रता होगी,

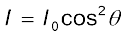जहाँ कोण θ, P1 एवं P2 की पारित-अक्षों के बीच बना कोण है| क्योंकि P1 एवं P3 क्रॉसित हैं उनके पारित-अक्षों के बीच कोण (π/2–θ) होगा| अतः P3 से निर्गमित होने वाले प्रकाश की तीव्रता होगी,

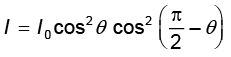
= I0 cos2θ sin2θ =(I0/4) sin22θ

अतः, कोण θ = π/4 के लिए पारगमित प्रकाश की तीव्रता अधिकतम होगी|

10.7.1 प्रकीर्णन के द्वारा ध्रुवण

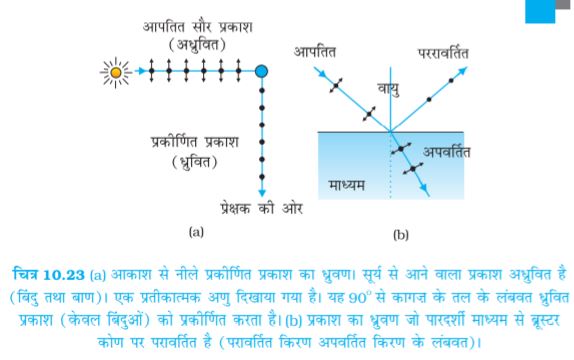
आकाश के एक साफ़ नीले भाग से आने वाले प्रकाश को जब एक घूमते हुए पोलेरॉइड में से होकर देखा जाता है तो तीव्रता बढ़ती तथा घटती हुई दिखाई देती है| यह और कुछ नहीं बल्कि सूर्य से आने वाला वह प्रकाश है जिसने पृथ्वी के वायुमंडल के अणुओं से टकराकर (प्रकीर्णन के कारण) अपनी दिशा बदल दी है| आपतित सूर्य का प्रकाश अध्रुवित है [चित्र 10.23(a)]| बिंदुओं के द्वारा चित्र के तल के लंबवत ध्रुवण को दर्शाया गया है| द्विशीर्ष बाण चित्र के तल में ध्रुवण को दर्शाते हैं| (अध्रुवित प्रकाश में इन दोनों में कोई कला-संबंध नहीं है|) आपतित तरंग के विद्युत क्षेत्र के प्रभाव में अणुओं में इलेक्ट्रॉन इन दोनों दिशाओें में गति ग्रहण कर लेते हैं| हमने सूर्य की दिशा के 90° पर देखते हुए एक प्रेक्षक को दर्शाया है| स्पष्टतः आवेश जो द्विशीर्ष बाणों के समांतर त्वरित हैं, इस प्रेक्षक की दिशा में ऊर्जा विकिरित नहीं करते क्योंकि उनके त्वरण का कोई अनुप्रस्थ घटक नहीं है| अणु के द्वारा प्रकीर्णित विकिरण को इसीलिए बिंदुओं से प्रस्तुत किया गया है| यह चित्र-तल के लंबवत ध्रुवित है| इससे आकाश से प्रकीर्णित प्रकाश के ध्रुवण की व्याख्या होती है|

अणुओं के द्वारा प्रकाश के प्रकीर्णन का गहन अध्ययन सी.वी. रमन तथा उनके सहयोगियों के द्वारा कोलकाता में 1920 के दशक में किया गया था| रमन को सन् 1930 में इस कार्य के लिए भौतिकी के नोबेल पुरस्कार से सम्मानित किया गया था|

10.7.2 परावर्तन के द्वारा ध्रुवण

चित्र 10.23 (b) एक पारदर्शी माध्यम जैसे जल से परावर्तित प्रकाश को दर्शाता है| पहले की भाँति बिंदु तथा बाण संकेत करते हैं कि आपतित तथा परावर्तित तरंगों में दोनों ही ध्रुवण मौजूद हैं| हमने एक एेसी स्थिति प्रस्तुत की है जिसमें परावर्तित किरण, अपवर्तित किरण के समकोण पर चलती है| जल में दोलनकारी इलेक्ट्रॉन परावर्तित तरंग उत्पन्न करते हैं| यह माध्यम तरंग के विकिरण, अर्थात अपवर्तित तरंग के अनुप्रस्थ दो दिशाओं में चलते हैं| बाण परावर्तित तरंग की दिशा के समांतर हैं| इस दिशा में गति परावर्तित तरंग को कोई योगदान नहीं देती| इसलिए, जैसा कि चित्र दर्शाता है, परावर्तित प्रकाश चित्र-तल के लंबवत रेखीय ध्रुवित है (बिंदुओं के द्वारा दिखाए गए)| इसकी जाँच परावर्तित प्रकाश को किसी विश्लेषक में से होकर आने वाले प्रकाश को देखकर की जा सकती है| जब विश्लेषक का अक्ष, चित्र-तल में (अर्थात आपतन तल में) होगा तो पारगमित तीव्रता शून्य होगी|

दो पारदर्शी माध्यमों की सीमा पर जब कोई अध्रुवित प्रकाश आपतित होता है, तब यदि अपवर्तित तथा परावर्तित किरणें एक-दूसरे के बीच समकोण बनाती हों, तो परावर्तित प्रकाश पूर्णतः ध्रुवित होता है तथा इसका विद्युत सदिश आपतन तल के लंबवत होता है| इस प्रकार हमने देखा कि जब परावर्तित तरंग अपवर्तित तरंग पर लंबवत है तो परावर्तित तरंग एक पूर्ण ध्रुवित तरंग है| इस अवस्था में आपतन कोण को ब्रूस्टर कोण कहते हैं तथा इसे iB से निरूपित करते हैं| हम देख सकते हैं कि iB सघन माध्यम के अपवर्तनांक से संबंधित है| क्योंकि iB+r = π/2 है, हमें स्नैल के नियम से प्राप्त होगा

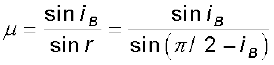
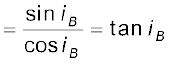(10.36)

इसे ब्रूस्टर का नियम कहते हैं|

उदाहरण 10.9 एक समतल काँच के पृष्ठ पर अध्रुवित प्रकाश आपतित होता है| आपतन कोण कितना होना चाहिए जिससे कि परावर्तित या अपवर्तित किरणें एक-दूसरे पर लंबवत हों|

हल i + r, π/2 के बराबर होने के लिए, tan iB = µ = 1.5 होना चाहिए| इससे
iB = 57° प्राप्त होता है| यह वायु से काँच के अंतरापृष्ठ पर ब्रूस्टर कोण है|

सरलता के लिए, हमने 90° पर प्रकाश के प्रकीर्णन तथा ब्रूस्टर कोण पर परावर्तन का विवेचन किया है| इस विशिष्ट परिस्थिति में, विद्युत क्षेत्र के दो लंबवत घटकों में से एक शून्य हो जाता है| अन्य कोणों पर, दोनों ही घटक विद्यमान होते हैं परंतु एक घटक दूसरे घटक से प्रबल होता है| दोनों लंबवत घटकों में कोई स्थिर कला संबंध नहीं होता है क्योंकि ये एक अध्रुवित किरण-पुंज के दो लंबवत घटकों से उत्पन्न होते हैं| जब एेसे प्रकाश को किसी घूर्णित विश्लेषक में से देखा जाता है तो तीव्रता का उच्चिष्ठ तथा निम्निष्ठ दिखाई देता है, परंतु पूर्ण अदीप्त नहीं हो पाता| इस प्रकार के प्रकाश को आंशिक ध्रुवित प्रकाश कहते हैं|

पूर्ण पारगमन की एक विशेष दशा

जब प्रकाश दो माध्यमों के अंतरापृष्ठ पर आपतित होता है तो यह देखा गया है कि इसका कुछ भाग परावर्तित हो जाता है तथा कुछ भाग पारगमित हो जाता है| इसी से संबंधित एक प्रश्न पर विचार करें ः क्या यह संभव है कि किसी दशा में किसी सतह पर आपतित होने वाला एकवर्णीय प्रकाश का एक किरण-पुंज (सतह सामान्यतः परावर्ती है) पूर्ण रूप से पारगमित हो जाए तथा कोई परावर्तन न हो? आपको आश्चर्य होगा कि इस प्रश्न का उत्तर "हाँ" है|

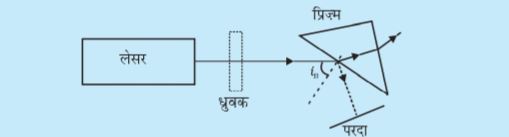
आइए, एक साधारण प्रयोग करें तथा जाँच करें कि क्या होता है| एक लेसर, एक अच्छा ध्रुवक (polarizer), एक प्रिज़्म तथा एक परदा दर्शाए गए चित्र की भाँति व्यवस्थित करें|

लेसर स्रोत से उत्सर्जित प्रकाश को ध्रुवक से पारित होने के पश्चात प्रिज़्म की सतह पर ब्रूस्टर कोण iB से आपतित होने दें| अब ध्रुवक को सावधानीपूर्वक घुमाएँ| आप देखेंगे कि ध्रुवक के एक विशेष संरेखन (alignment) के लिए प्रिज़्म पर आपतित होने वाला प्रकाश पूर्ण रूप से पारगमित हो जाता है तथा प्रिज़्म के पृष्ठ से कोई प्रकाश परावर्तित नहीं होता| परावर्तित धब्बा पूरी तरह अदृश्य हो जाता है|

आइए, इस स्थिति को समझने का प्रयत्न करें| जब दो माध्यमों के अंतरापृष्ठ पर एक अध्रुवित प्रकाश का किरण-पुंज ब्रूस्टर कोण पर आपतित होता है, प्रकाश का केवल एक भाग, जिसका विद्युत क्षेत्र सदिश आपतन तल के लंबवत है, परावर्तित होगा| अब यदि एक अच्छे ध्रुवक (Polarizer) का उपयोग करके, आपतन तल के लंबवत प्रकाश के विद्युत सदिश को पूर्णतया पृथक कर दें तथा इस प्रकाश को ब्रूस्टर कोण पर प्रिज़्म के पृष्ठ पर आपतित कराएँ, तब आप परावर्तन बिलकुल नहीं देख पाएँगे तथा प्रकाश का पूर्ण परागमन होगा|

इस अध्याय को हमने यह संकेत करते हुए प्रारंभ किया कि कुछ परिघटनाएँ एेसी हैं जिनकी व्याख्या केवल तरंग सिद्धांत द्वारा की जा सकती है| उचित रूप से समझने के लिए हमने पहले परावर्तन तथा अपवर्तन जैसी परिघटनाओं का, जिनका हम किरण प्रकाशिकी के आधार पर अध्याय 9 में अध्ययन कर चुके थे, वर्णन किया तथा देखा कि इन्हें तरंग प्रकाशिकी के आधार पर भी समझा जा सकता है| फिर हमने यंग के द्विझिरी प्रयोग का वर्णन किया जो कि प्रकाशिकी के अध्ययन का एक मोड़ था| अंत में हमने कुछ संबंधित विषयों जैसे विवर्तन, विभेदन, ध्रुवण तथा किरण प्रकाशिकी की वैधता का वर्णन किया| अगले अध्याय में आप देखेंगे कि शताब्दी के समाप्त होते-होते लगभग 1900 ई. में किस प्रकार नए प्रयोगों ने नए सिद्धांतों को जन्म दिया|

सारांश

1. हाइगेंस का सिद्धांत बतलाता है कि किसी तरंगाग्र का प्रत्येक बिंदु द्वितीयक तरंगों का स्रोत होता है, जो जुड़कर कुछ समय पश्चात एक तरंगाग्र बनाते हैं|

2. हाइगेंस की रचना हमें यह बतलाती है कि नया तरंगाग्र द्वितीयक तरंगों का अग्र आवरण है| जब प्रकाश की चाल दिशा पर निर्भर नहीं करती हो तो द्वितीयक तरंगें गोलीय होती हैं| किरणें तब दोनों तरंगाग्रों के लंबवत होती हैं तथा यात्रा काल किसी भी किरण की दिशा में समान होता है| इस सिद्धांत से परावर्तन तथा अपवर्तन के सुज्ञात नियम प्राप्त होते हैं|

3. जब दो अथवा दो से अधिक प्रकाश स्रोत एक ही बिंदु को प्रदीप्त करते हैं तो तरंगों के अध्यारोपण का सिद्धांत लागू होता है| जब हम एक बिंदु पर इन स्रोतों द्वारा प्रकाश की तीव्रता का विचार करते हैं तो विशिष्ट तीव्रताओं के योग के अतिरिक्त एक व्यतिकरण पद प्राप्त होता है| परंतु यह पद तभी महत्वपूर्ण होता है जबकि इसका औसत शून्य नहीं है, जो केवल तभी होता है जबकि स्रोतों की आवृत्तियाँ समान हों तथा इनके बीच एक स्थिर कलांतर हो|

4. पृथकता d वाली टॉमस यंग की द्विझिरी से समान अंतराल की फ्रिंजें प्राप्त होती हैं जिनकी कोणीय पृथकता λ/d होती है| स्रोत, झिरियों का मध्यबिंदु तथा केंद्रीय दीप्त फ्रिंज एक सीधी रेखा में होते हैं| एक बड़े आकार का स्रोत जो झिरियों पर λ/d से अधिक कोण बनाता है, फ्रिंजों को विलुप्त कर देगा|

5. चौड़ाई a की एक एकल झिरी एक विवर्तन पैटर्न देती है जिसमें एक केंद्रीय उच्चिष्ठ होता है| तीव्रता 3050.pngλ/a, 3055.png2λ/a, आदि कोणों पर शून्य होती है तथा इनके बीच में उत्तरोत्तर क्षीण होते द्वितीयक उच्चिष्ठ होते हैं| विवर्तन किसी दूरदर्शी के कोणीय विभेदन को λ/D तक परिसीमित कर देता है, जहाँ D द्वारक का व्यास है| दो तारें जिनके बीच की दूरी इससे कम होगी प्रबलतः अतिव्यापी प्रतिबिंब बनाएँगे| इसी प्रकार, एक सूक्ष्मदर्शी अभिदृश्यक जो n अपवर्तनांक के माध्यम में फ़ोकस बिंदु पर कोण 2β बनाता है, दो वस्तुओं जिनके बीच की दूरी λ/(2n sin β) है, को ठीक-ठीक पृथक करेगा, जोकि सूक्ष्मदर्शी की विभेदन सीमा है| विवर्तन प्रकाश किरणों की संकल्पना की सीमा निर्धारित करता है| इससे पहले कि विवर्तन के कारण प्रकाश प्रसरित होना प्रारंभ करे चौड़ाई a का एक किरण-पुंज एक दूरी a2/λ चलता है जो फ्रेनेल दूरी कहलाती है|

6. प्राकृतिक प्रकाश, जैसे सूर्य से प्राप्त प्रकाश, अध्रुवित होता है| इसका अर्थ यह हुआ कि अनुप्रस्थ तल में विद्युत सदिश मापन के समय, द्रुततः तथा यादृच्छिकतः सभी संभव दिशाओं में हो सकता है| पोलेरॉइड केवल एक घटक (एक विशिष्ट अक्ष के समांतर) को पारगमित करता है| परिणामी प्रकाश को रेखीय ध्रुवित अथवा समतल ध्रुवित कहते हैं| जब इस प्रकार के प्रकाश को एक दूसरे पोलेरॉइड में से देखते हैं, जिसका अक्ष 2π से घूमता है तो तीव्रता के दो उच्चिष्ठ तथा निम्निष्ठ दिखलाई देते हैं| ध्रुवित प्रकाश एक विशिष्ट कोण (जिसे ब्रूस्टर कोण कहते हैं) पर परावर्तन के द्वारा तथा पृथ्वी के वायुमंडल में π/2 के प्रकीर्णन द्वारा भी उत्पन्न किया जा सकता है|

विचारणीय विषय

1. एक बिंदु स्रोत से तरंगें सभी दिशाओं में प्रसरित होती हैं, जबकि प्रकाश को संकीर्ण किरणों के रूप में चलते हुए देखा गया था| तरंग सिद्धांत से प्रकाश के व्यवहार के सभी पक्षों के विश्लेषण को समझने के लिए हाइगेंस, यंग तथा फ्रेनेल के प्रयोगों तथा अंतर्दृष्टि की आवश्यकता हुई|

2. तरंगों का महत्वपूर्ण तथा नया स्वरूप भिन्न स्रोतों के आयामों का व्यतिकरण है, जो यंग के प्रयोग में दर्शाए अनुसार संपोषी तथा विनाशी दोनों हो सकता है|

3. विवर्तन परिघटना से किरण प्रकाशिकी की परिसीमा परिभाषित होती है| दो बहुत निकटस्थ वस्तुओं के विभेदन के लिए सूक्ष्मदर्शियों तथा दूरदर्शियों की सक्षमता की सीमाएँ भी प्रकाश की तरंगदैर्घ्य द्वारा निर्धारित होती हैं|

4. अधिकांश व्यतिकरण तथा विवर्तन प्रभाव अनुदैर्घ्य तरंगों, जैसे वायु में ध्वनि के लिए भी होते हैं| परंतु ध्रुवण परिघटना केवल अनुप्रस्थ तरंगों, जैसे प्रकाश तरंगों की, विशिष्टता है|

अभ्यास

10.1 589 nm तरंगदैर्घ्य का एकवर्णीय प्रकाश वायु से जल की सतह पर आपतित होता है|
(a) परावर्तित तथा (b) अपवर्तित प्रकाश की तरंगदैर्घ्य, आवृत्ति तथा चाल क्या होगी? जल का आवर्तनांक 1.33 है|

10.2 निम्नलिखित दशाओं में प्रत्येक तरंगाग्र की आकृति क्या है?

(a) किसी बिंदु स्रोत से अपसरित प्रकाश|

(b) उत्तल लेंस से निर्गमित प्रकाश, जिसके फ़ोकस बिंदु पर कोई बिंदु स्रोत रखा है|

10.3 (a) काँच का अपवर्तनांक 1.5 है| काँच में प्रकाश की चाल क्या होगी? (निर्वात में प्रकाश की चाल 3.0 × 108 m s–1 है|)

(b) क्या काँच में प्रकाश की चाल, प्रकाश के रंग पर निर्भर करती है? यदि हाँ, तो लाल तथा बैंगनी में से कौन-सा रंग काँच के प्रिज़्म में धीमा चलता है?

10.4 यंग के द्विझिरी प्रयोग में झिरियों के बीच की दूरी 0.28 mm है तथा परदा 1.4 m की दूरी पर रखा गया है| केंद्रीय दीप्त फ्रिंज एवं चतुर्थ दीप्त फ्रिंज के बीच की दूरी 1.2 cm मापी गई है| प्रयोग में उपयोग किए गए प्रकाश की तरंगदैर्घ्य ज्ञात कीजिए|

10.5 यंग के द्विझिरी प्रयोग में, λ तरंगदैर्घ्य का एकवर्णीय प्रकाश उपयोग करने पर, परदे के एक बिंदु पर जहाँ पथांतर λ है, प्रकाश की तीव्रता K इकाई है| उस बिंदु पर प्रकाश की तीव्रता कितनी होगी जहाँ पथांतर λ/3 है?

10.6 यंग के द्विझिरी प्रयोग में व्यतिकरण फ्रिंजों को प्राप्त करने के लिए, 650 nm तथा 520 nm तरंगदैर्घ्यों के प्रकाश-पुंज का उपयोग किया गया|

(a) 650 nm तरंगदैर्घ्य के लिए परदे पर तीसरे दीप्त फ्रिंज की केंद्रीय उच्चिष्ठ से दूरी ज्ञात
कीजिए|

(b) केंद्रीय उच्चिष्ट से उस न्यूनतम दूरी को ज्ञात कीजिए जहाँ दोनों तरंगदैर्घ्यों के कारण दीप्त
फ्रिंज संपाती (coincide) होते हैं|

10.7 एक द्विझिरी प्रयोग में एक मीटर दूर रखे परदे पर एक फ्रिंज की कोणीय चौड़ाई 0.2° पाई गई| उपयोग किए गए प्रकाश की तरंगदैर्घ्य 600 nm है| यदि पूरा प्रायोगिक उपकरण जल में डुबो दिया जाए तो फ्रिंज की कोणीय चौड़ाई क्या होगी? जल का अपवर्तनांक 4/3 लीजिए|

10.8 वायु से काँच में संक्रमण (transition) के लिए ब्रूस्टर कोण क्या है? (काँच का
अपवर्तनांक = 1.5)|

10.9 5000 Å तरंगदैर्घ्य का प्रकाश एक समतल परावर्तक सतह पर आपतित होता है| परावर्तित प्रकाश की तरंगदैर्घ्य एवं आवृत्ति क्या है? आपतन कोण के किस मान के लिए परावर्तित किरण आपतित किरण के लंबवत होगी?

10.10 उस दूरी का आकलन कीजिए जिसके लिए किसी 4 mm के आकार के द्वारक तथा 400 nm तरंगदैर्घ्य के प्रकाश के लिए किरण प्रकाशिकी सन्निकट रूप से लागू होती है|

अतिरिक्त अभ्यास

10.11 एक तारे में हाइड्रोजन से उत्सर्जित 6563 Å की Hα लाइन में 15 Å का अभिरक्त-विस्थापन (red-shift) होता है| पृथ्वी से दूर जा रहे तारे की चाल का आकलन कीजिए|

10.12 किसी माध्यम (जैसे जल) में प्रकाश की चाल निर्वात में प्रकाश की चाल से अधिक है| न्यूटन के कणिका सिद्धांत द्वारा इस आशय की भविष्यवाणी कैसे की गई| क्या जल में प्रकाश की चाल प्रयोग द्वारा ज्ञात करके इस भविष्यवाणी की पुष्टि हुई? यदि नहीं, तो प्रकाश के चित्रण का कौन-सा विकल्प प्रयोगानुकूल है|

10.13 आप मूल पाठ में जान चुके हैं कि हाइगेंस का सिद्धांत परावर्तन और अपवर्तन के नियमों के लिए किस प्रकार मार्गदर्शक है| इसी सिद्धांत का उपयोग करके प्रत्यक्ष रीति से निगमन (deduce) कीजिए कि समतल दर्पण के सामने रखी किसी वस्तु का प्रतिबिंब आभासी बनता है, जिसकी दर्पण से दूरी, बिंब से दर्पण की दूरी के बराबर होती है|

10.14 तरंग संचरण की चाल को प्रभावित कर सकने वाले कुछ संभावित कारकों की सूची है ः

(i) स्रोत की प्रकृति,

(ii) संचरण की दिशा,

(iii) स्रोत और/या प्रेक्षक की गति,

(iv) तरंगदैर्घ्य, तथा

(v) तरंग की तीव्रता|

बताइए कि–

(a) निर्वात में प्रकाश की चाल,

(b) किसी माध्यम (माना काँच या जल) में प्रकाश की चाल इनमें से किन कारकों पर निर्भर करती है?

10.15 ध्वनि तरंगों में आवृत्ति विस्थापन के लिए डॉप्लर का सूत्र निम्नलिखित दो स्थितियों में थोड़ा-सा भिन्न है ः (i) स्रोत विरामावस्था में तथा प्रेक्षक गति में हो, तथा (ii) स्रोत गति में परंतु प्रेक्षक विरामावस्था में हो| जबकि प्रकाश के लिए डॉप्लर के सूत्र निश्चित रूप से निर्वात में, इन दोनों स्थितियों में एकसमान हैं| एेसा क्यों है? स्पष्ट कीजिए| क्या आप समझते हैं कि ये सूत्र किसी माध्यम में प्रकाश गमन के लिए भी दोनों स्थितियों में पूर्णतः एकसमान होंगे?

10.16 द्विझिरी प्रयोग में, 600 nm तरंगदैर्घ्य का प्रकाश करने पर, एक दूरस्थ परदे पर बने फ्रिंज की कोणीय चौड़ाई 0.1º है| दोनों झिरियों के बीच कितनी दूरी है?

10.17 निम्नलिखित प्रश्नों के उत्तर दीजिए ः

(a) एकल झिरी विवर्तन प्रयोग में, झिरी की चौड़ाई मूल चौड़ाई से दोगुनी कर दी गई है| यह केंद्रीय विवर्तन बैंड के साइज़ तथा तीव्रता को कैसे प्रभावित करेगी?

(b) द्विझिरी प्रयोग में, प्रत्येक झिरी का विवर्तन, व्यतिकरण पैटर्न से किस प्रकार संबंधित है?

(c) सुदूर स्रोत से आने वाले प्रकाश के मार्ग में जब एक लघु वृत्ताकार वस्तु रखी जाती है तो वस्तु की छाया के मध्य एक प्रदीप्त बिंदु दिखाई देता है| स्पष्ट कीजिए क्यों?

(d) दो विद्यार्थी एक 10 m ऊँची कक्ष विभाजक दीवार द्वारा 7 m के अंतर पर हैं| यदि ध्वनि और प्रकाश दोनों प्रकार की तरंगें वस्तु के किनारों पर मुड़ सकती हैं तो फिर भी वे विद्यार्थी एक-दूसरे को देख नहीं पाते यद्यपि वे आपस में आसानी से वार्तालाप किस प्रकार कर पाते हैं?

(e) किरण प्रकाशिकी, प्रकाश के सीधी रेखा में गति करने की संकल्पना पर आधारित है| विवर्तन प्रभाव (जब प्रकाश का संचरण एक द्वारक/झिरी या वस्तु के चारों ओर प्रेक्षित किया जाए) इस संकल्पना को नकारता है| तथापि किरण प्रकाशिकी की संकल्पना प्रकाशकीय यंत्रों में प्रतिबिंबों की स्थिति तथा उनके दूसरे अनेक गुणों को समझने के लिए सामान्यतः उपयोग में लाई जाती है| इसका क्या औचित्य है?

10.18 दो पहाड़ियों की चोटी पर दो मीनारें एक-दूसरे से 40 km की दूरी पर हैं| इनको जोड़ने वाली रेखा मध्य में आने वाली किसी पहाड़ी के 50 m ऊपर से होकर गुज़रती है| उन रेडियो तरंगों की अधिकतम तरंगदैर्घ्य ज्ञात कीजिए, जो मीनारों के मध्य बिना पर्याप्त विवर्तन प्रभाव के भेजी जा सकें|

10.19 500 nm तरंगदैर्घ्य का एक समांतर प्रकाश-पुंज एक पतली झिरी पर गिरता है तथा 1 m दूर परदे पर परिणामी विवर्तन पैटर्न देखा जाता है| यह देखा गया कि पहला निम्निष्ठ परदे के केंद्र से 2.5 mm दूरी पर है| झिरी की चौड़ाई ज्ञात कीजिए|

10.20 निम्नलिखित प्रश्नों के उत्तर दीजिए ः

(a) जब कम ऊँचाई पर उड़ने वाला वायुयान ऊपर से गुज़रता है तो हम कभी-कभी टेलीविज़न के परदे पर चित्र को हिलते हुए पाते हैं| एक संभावित स्पष्टीकरण सुझाइए|

(b) जैसा कि आप मूल पाठ में जान चुके हैं कि विवर्तन तथा व्यतिकरण पैटर्न में तीव्रता का वितरण समझने का आधारभूत सिद्धांत तरंगों का रेखीय प्रत्यारोपण है| इस सिद्धांत की तर्कसंगति क्या है?

10.21 एकल झिरी विवर्तन पैटर्न की व्युत्पत्ति में कथित है कि nλ/a कोणों पर तीव्रता शून्य है| इस निरसन (cancillation) को, झिरी को उपयुक्त भागों में बाँटकर सत्यापित कीजिए|

Table of Contents

अध्याय 10

तरंग-प्रकाशिकी

10.1 भूमिका

क्या प्रकाश सीधी रेखा में चलता है?

10.3.1 समतल तरंगों का अपवर्तन

10.3.2 विरल माध्यम पर अपवर्तन

10.3.3 समतल पृष्ठ से एक समतल तरंग का परावर्तन

10.3.4 डॉप्लर प्रभाव

10.6.1 एकल झिरी

10.6.2 एकल झिरी विवर्तन पैटर्न का अवलोकन

10.6.3 प्रकाशिक यंत्रों की विभेदन क्षमता

10.6.4 किरण प्रकाशिकी की वैधता

10.7.1 प्रकीर्णन के द्वारा ध्रुवण

10.7.2 परावर्तन के द्वारा ध्रुवण

अभ्यास