Table of Contents
अध्याय 11
विकिरण तथा द्रव्य की द्वैत प्रकृति
11.1 भूमिका
सन् 1887 में वैद्युतचुंबकीय किरणों की उत्पत्ति एवं संसूचना पर विद्युत चुंबकत्व के मैक्सवेल समीकरण तथा हर्ट्ज़ के प्रयोगों ने प्रकाश की तरंगीय प्रकृति को अभूतपूर्व रूप से स्थापित किया| उन्नीसवीं शताब्दी के अंतिम चरण में विसर्जन-नलिका में गैसों में कम दाब पर विद्युत-चालन (विद्युत-विसर्जन) पर प्रायोगिक अन्वेषणों से कई एेतिहासिक खोजें हुईं| रूंटगेन के द्वारा 1895 में X-किरणों की खोज तथा जे. जे. टॉमसन के द्वारा 1897 में की गई इलेक्ट्रॉन की खोज परमाणु-संरचना को समझने में मील का पत्थर थीं| लगभग 0.001 mm पारे के स्तंभ के अत्यंत कम दाब पर यह पाया गया कि एेसे दो इलेक्ट्रोडों के बीच, जिनके द्वारा विसर्जन-नलिका में गैस पर विद्युत क्षेत्र स्थापित किया जाता है, एक विसर्जन होता है| कैथोड के सम्मुख काँच पर प्रतिदीप्त उत्पन्न होती है| दीप्त का रंग काँच की प्रकृति पर निर्भर करता है, जैसे–सोडा-काँच के लिए पीत-हरा रंग का| इस प्रतिदीप्ति का कारण उस विकिरण को माना गया जो कैथोड से आ रहा था| ये कैथोड किरणें 1870 में विलियम क्रुक्स के द्वारा खोजी गई थीं, जिसने बाद में 1879 में यह सुझाया कि ये किरणें तीव्रता से चलने वाली ऋण-आवेशी कणों की धारा से बनी हैं| ब्रिटिश भौतिक शास्त्री जे.जे. टॉमसन (1856 – 1940) ने इस परिकल्पना की पुष्टि की| जे.जे. टॉमसन ने पहली बार विसर्जन-नलिका के आर-पार परस्पर लंबवत विद्युत एवं चुंबकीय क्षेत्रों को स्थापित कर प्रायोगिक तौर पर कैथोड-किरण कणों के वेग तथा आपेक्षिक आवेश [अर्थात आवेश और द्रव्यमान का अनुपात (e/m)] ज्ञात किया| यह पाया गया कि ये कण प्रकाश के वेग (3 ×108 m/s) के लगभग 0.1 से लेकर 0.2 गुने वेग से चलते हैं| वर्तमान में e/m का स्वीकृत मान 1.76 × 1011 C/kg है| यह भी पाया गया कि e/m का मान कैथोड (उत्सर्जक) के पदार्थ अथवा धातु या विसर्जन-नलिका में भरी गैस की प्रकृति पर निर्भर नहीं करता| इस प्रेक्षण ने कैथोड-किरण कणों की सार्विकता को सुझाया|
लगभग उसी समय, 1887 में, यह पाया गया कि जब कुछ निश्चित धातुओं को पराबैंगनी प्रकाश द्वारा किरणित करते हैं तो कम वेग वाले ऋण-आवेशित कण उत्सर्जित होते हैं| इसी प्रकार, जब कुछ निश्चित धातुओं को उच्च ताप तक गरम किया जाता है तो ये ऋण-आवेशित कण उत्सर्जित करते हैं| इन कणों के लिए e/m का मान उतना ही पाया गया जितना कि कैथोड किरण कणों का था| इस प्रकार इन प्रेक्षणों ने यह स्थापित कर दिया कि ये सभी कण, यद्यपि भिन्न दशाओं में उत्पन्न हुए थे, प्रकृति में समान थे| जे.जे. टॉमसन ने, 1897 में, इन कणों को इलेक्ट्रॉन नाम दिया और सुझाया कि ये द्रव्य के मौलिक सार्वत्रिक अवयव हैं| गैसों में विद्युत के संवहन पर उनके सैद्धांतिक तथा प्रायोगिक प्रेक्षणों के द्वारा इलेक्ट्रॉन की इस युगांतकारी खोज के लिए उन्हें 1906 में नोबेल पुरस्कार प्रदान किया गया| 1913 में अमेरिकी भौतिकविज्ञानी आर.ए. मिलिकन (1868– 1953) ने इलेक्ट्रॉन पर आवेश के परिशुद्ध मापन के लिए तेल-बूँद का पथ प्रदर्शक प्रयोग किया| उन्होंने यह पाया कि तेल-बिंदुक पर आवेश सदैव एक मूल आवेश, 1.602 × 10–19 C का पूर्ण गुणांक है| मिलिकन के प्रयोग ने यह प्रस्थापित कर दिया कि वैद्युतआवेश क्वांटीकृत है| आवेश (e) तथा आपेक्षित आवेश (e/m) के मान से, इलेक्ट्रॉन का द्रव्यमान (m) ज्ञात किया जा सका|
11.2 इलेक्ट्रॉन उत्सर्जन
हम जानते हैं कि धातुओं में मुक्त इलेक्ट्रॉन (ऋण आवेशित कण) होते हैं जो उनकी चालकता के लिए उत्तरदायी होते हैं| तथापि, मुक्त इलेक्ट्रॉन सामान्यतः धातु-पृष्ठ से बाहर नहीं निकल सकते| यदि इलेक्ट्रॉन धातु से बाहर आते हैं तो इसका पृष्ठ धन आवेश प्राप्त कर लेता है और इलेक्ट्रॉनों को वापस धातु पर आकर्षित कर लेता है| इस प्रकार मुक्त इलेक्ट्रॉन धातु के भीतर आयनों के आकर्षण बलों के द्वारा रोककर रखे गए होते हैं| परिणामस्वरूप सिर्फ़ वे इलेक्ट्रॉन जिसकी ऊर्जा इस आकर्षण को अभिभूत कर सके, धातु पृष्ठ से बाहर आ पाते हैं| अतः इलेक्ट्रॉनों को धातु पृष्ठ से बाहर निकालने के लिए एक निश्चित न्यूनतम ऊर्जा की आवश्यकता होती है| इस न्यूनतम ऊर्जा को धातु का कार्य-फलन कहते हैं| इसे साधारणतया φο के द्वारा व्यक्त करते हैं और eV (इलेक्ट्रॉन वोल्ट) में मापते हैं| एक इलेक्ट्रॉन वोल्ट किसी इलेक्ट्रॉन को 1 वोल्ट विभवांतर के द्वारा त्वरित कराने पर प्राप्त ऊर्जा का मान है| अतः 1 eV = 1.602 × 10–19 J
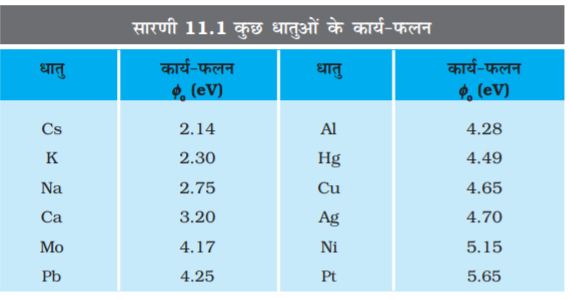
साधारणतया ऊर्जा की इस इकाई का प्रयोग परमाणु तथा नाभिकीय भौतिकी में किया जाता है| कार्य-फलन (φ0) धातु के गुणों और इसके पृष्ठ की प्रकृति पर निर्भर करता है| कुछ धातुओं के कार्य-फलन के मान सारणी 11.1 में दिए गए हैं| ये मान अनुमानित हैं क्योंकि इनके मान पृष्ठीय अपद्रव्यों पर बहुत अधिक निर्भर करते हैं|
सारणी 11.1 से यह ध्यान किया जा सकता है कि प्लैटिनम का कार्य-फलन उच्चतम(φ0 = 5.65 eV) है जबकि सीज़ियम का न्यूनतम (φ0 = 2.14 eV) है|
धातु के पृष्ठ से इलेक्ट्रॉन उत्सर्जन के लिए मुक्त इलेक्ट्रॉनों को न्यूनतम आवश्यक ऊर्जा निम्न किसी भी एक भौतिक विधि के द्वारा दी जा सकती है :
(i) तापायनिक उत्सर्जन : उपयुक्त तापन के द्वारा मुक्त इलेक्ट्रॉनों को पर्याप्त तापीय ऊर्जा दी जा सकती है जिससे कि वे धातु से बाहर आ सकें|
(ii) क्षेत्र उत्सर्जन : किसी धातु पर लगाया गया एक प्रबल विद्युत क्षेत्र (108 V m–1 की कोटि का) इलेक्ट्रॉनों को धातु-पृष्ठ के बाहर ला सकता है, जैसा कि किसी स्पार्क प्लग में|
(iii) प्रकाश-विद्युत उत्सर्जन : उपयुक्त आवृत्ति का प्रकाश जब किसी धातु-पृष्ठ पर पड़ता है तो इलेक्ट्रॉनों का उत्सर्जन होता है| ये प्रकाशजनित इलेक्ट्रॉन प्रकाशिक इलेक्ट्रॉन (photo-electron) कहलाते हैं|
11.3 प्रकाश-विद्युत प्रभाव
11.3.1 हट्ज़ के परीक्षण
प्रकाश-विद्युत उत्सर्जन की परिघटना की खोज हेनरिच हट्ρज़ (1857-1894) के द्वारा 1887 में वैद्युतचुंबकीय तरंगों के प्रयोगाें के समय की गई थी| स्फुलिंग-विसर्जन (spark discharge) के द्वारा वैद्युतचुंबकीय तरंगों की उत्पत्ति के अपने प्रायोगिक अन्वेषण में हर्ट्ज़ ने यह प्रेक्षित किया कि कैथोड को किसी आर्क लैंप से पराबैंगनी प्रकाश के द्वारा प्रदीप्त करने पर धातु-इलेक्ट्रोडों के पार उच्च वोल्टता स्फुलिंग अधिक हो जाता है|
धातु-पृष्ठ पर चमकने वाला प्रकाश मुक्त आवेशित कणों जिन्हें अब हम इलेक्ट्रॉन कहते हैं, को स्वतंत्र करने में सहायता प्रदान करता है| जब धातु-पृष्ठ पर प्रकाश पड़ता है तो पृष्ठ के समीप इलेक्ट्रॉन आपतित विकिरण से पदार्थ के पृष्ठ में धनात्मक आयनों के आकर्षण को पार करने के लिए ऊर्जा अवशोषित कर लेते हैं| आपतित प्रकाश से आवश्यक ऊर्जा प्राप्त करने के पश्चात, इलेक्ट्रॉन धातु-पृष्ठ से बाहर परिवेश में आ जाते हैं|
11.3.2 हालवॉक्स तथा लीनार्ड के प्रेक्षण
विलहेल्म हालवॉक्स तथा फिलिप लीनार्ड ने 1886-1902 के बीच प्रकाशविद्युत उत्सर्जन की परिघटना का अन्वेषण किया|
दो इलेक्ट्रोडों (धातु पट्टिकाओं) वाली किसी निर्वातित काँच की नली में उत्सर्जक पट्टिका पर पराबैंगनी विकिरणों को आपतित करने पर लीनार्ड (1862-1947) ने पाया कि परिपथ में धारा प्रवाह होता है (चित्र 11.1)| जैसे ही पराबैंगनी विकिरणों को रोका गया, वैसे ही धारा प्रवाह भी रुक गया| इन परीक्षणों से ज्ञात होता है कि जब पराबैंगनी विकिरण उत्सर्जक पट्टिका C पर आपतित होते हैं, इलेक्ट्रॉन पट्टिका से बाहर आ जाते हैं तथा विद्युत क्षेत्र द्वारा धनात्मक संग्राहक पट्टिका A की ओर आकर्षित हो जाते हैं| निर्वातित काँच की नली में इलेक्ट्रॉनों के प्रवाह के कारण धाराप्रवाह होती है| इस प्रकार से, उत्सर्जक के पृष्ठ पर प्रकाश पड़ने के कारण बाह्य परिपथ में धाराप्रवाह होती है| हालवॉक्स तथा लीनार्ड ने संग्राहक पट्टिका के विभव, आपतित प्रकाश की आवृत्ति तथा तीव्रता के साथ प्रकाश धारा में परिवर्तन का अध्ययन किया|
हालवॉक्स ने 1888 में इस अध्ययन को आगे बढ़ाया और एक ऋणावेशित जिंक पट्टिका को एक विद्युतदर्शी से जोड़ दिया| उसने प्रेक्षित किया कि जब पट्टिका को पराबैंगनी प्रकाश से किरणित किया गया तो इसने अपना आवेश खो दिया| इसके अतिरिक्त जब एक अनावेशित जिंक पट्टिका को पराबैंगनी प्रकाश से किरणित किया गया तो यह धनावेशित हो गई| जिंक पट्टिका को पराबैंगनी प्रकाश से पुनः किरणित करने पर, इस पट्टिका पर धनआवेश और अधिक हो गया| इन प्रेक्षणों से उसने यह निष्कर्ष निकाला कि पराबैंगनी प्रकाश के प्रभाव से जिंक पट्टिका से ऋणावेशित कण उत्सर्जित होते हैं|
1897 में इलेक्ट्रॉन की खोज के पश्चात यह निश्चित हो गया कि उत्सर्जक पट्टिका से इलेक्ट्रॉनों के उत्सर्जन का कारक आपतित प्रकाश है| ऋण आवेश के कारण उत्सर्जित इलेक्ट्रॉन विद्युत क्षेत्र द्वारा संग्राहक पट्टिका की ओर धकेले जाते हैं| हालवॉक्स तथा लीनार्ड ने यह भी प्रेक्षित किया कि जब उत्सर्जक पट्टिका पर एक नियत न्यूनतम मान से कम आवृत्ति का पराबैंगनी प्रकाश पड़ता है तो कोई भी इलेक्ट्रॉन उत्सर्जित नहीं होता| इस नियत न्यूनतम आवृत्ति को देहली आवृत्ति (threshold frequency) कहते हैं तथा इसका मान उत्सर्जक पट्टिका के पदार्थ की प्रकृति पर निर्भर करता है|
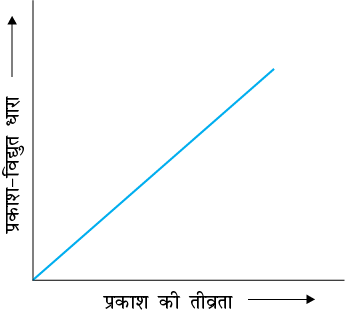
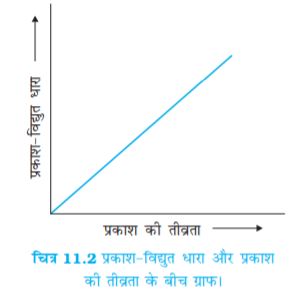
चित्र 11.2 प्रकाश-विद्युत धारा और प्रकाश की तीव्रता के बीच ग्राफ|
यह पाया गया कि जिंक, कैडमियम, मैग्नीशियम जैसी कुछ धातुओं मेें यह प्रभाव केवल कम तरंगदैर्घ्य की पराबैंगनी तरंगों के लिए होता है| तथापि लीथियम, सोडियम, पोटेशियम, सीजियम तथा रूबीडियम जैसी क्षार धातुएँ दृश्य प्रकाश के द्वारा भी यह प्रभाव दर्शाती हैं| जब इन प्रकाश-संवेदी पदार्थों को प्रकाश से प्रदीप्त किया जाता है तो ये इलेक्ट्रॉन उत्सर्जित करते हैं| इलेक्ट्रॉन की खोज के पश्चात् इन इलेक्ट्रॉनों को प्रकाशिक इलेक्ट्रॉन नाम दिया गया| यह परिघटना प्रकाश-विद्युत प्रभाव कहलाती है|
11.4 प्रकाश-विद्युत प्रभाव का प्रायोगिक अध्ययन
चित्र 11.1 में प्रकाश-विद्युत प्रभाव के प्रायोगिक अध्ययन के लिए उपयोग में लाई गई व्यवस्था को दर्शाया गया है| इसमें एक निर्वातित काँच/क्वार्टज़ की नली है जिसमें एक प्रकाश-संवेदी पट्टिका C और दूसरी धातु पट्टिका A है| स्रोत S से प्रकाश, गवाक्ष (window) W से पार होता है और पतली प्रकाश-संवेदी पट्टिका (उत्सर्जक) C पर पड़ता है| पारदर्शी क्वार्ट्ज़ गवाक्ष (काँच-नली पर मुद्रित) से पराबैंगनी विकिरण पार हो जाता है और प्रकाश-संवेदी पट्टिका C को किरणित करता है| पट्टिका C से इलेक्ट्रॉन उत्सर्जित होते हैं जो पट्टिका A (संग्राहक) पर बैटरी द्वारा उत्पन्न विद्युत क्षेत्र द्वारा एकत्र कर लिए जाते हैं| C तथा A पट्टिकाओं के बीच विभवांतर को बैटरी द्वारा बनाए रखा जाता है तथा इसे परिवर्तित किया जा सकता है| प्लेट C तथा A के ध्रुव दिशा दिक्परिवर्तक (Commutator) के द्वारा बदले जा सकते हैं| इस प्रकार उत्सर्जक पट्टिका C की तुलना में पट्टिका A को इच्छानुसार धन अथवा ऋण विभव पर रखा जा सकता है| जब संग्राहक पट्टिका A, उत्सर्जक पट्टिका C की तुलना में धनात्मक होगी तब इलेक्ट्रॉन इसकी ओर आकर्षित होंगे| इलेक्ट्रॉनों के उत्सर्जन के कारण विद्युत परिपथ में एक प्रवाह उत्पन्न होता है जिससे परिपथ में एक विद्युत धारा स्थापित हो जाती है| इलेक्ट्रोडों के बीच के विभवांतर को एक वोल्टमीटर के द्वारा और परिणामस्वरूप परिपथ में प्रवाहित होने वाली प्रकाशिक धारा को माइक्रोएेमीटर के द्वारा मापते हैं| प्रकाशिक विद्युत धारा को संग्राहक पट्टिका A का विभव उत्सर्जक पट्टिका C के सापेक्ष परिवर्तित करके बढ़ाया अथवा घटाया जा सकता है| आपतित प्रकाश की तीव्रता तथा आवृत्ति को भी परिवर्तित किया जा सकता है जैसे कि उत्सर्जक C और संग्राहक A के बीच विभवांतर V को परिवर्तित किया जाता है|
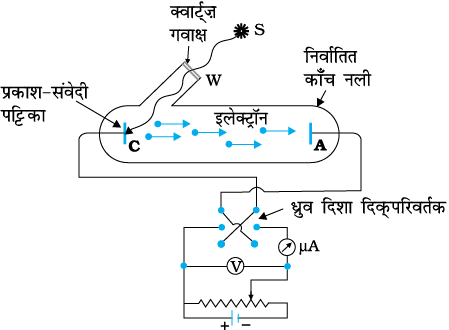
चित्र 11.1 प्रकाश-विद्युत प्रभाव के अध्ययन के लिए प्रायोगिक व्यवस्था|
हम चित्र 11.1 की प्रायोगिक व्यवस्था का उपयोग प्रकाशिक धारा के (a) विकिरण की तीव्रता, (b) आपतित विकिरण की आवृत्ति, (c) पट्टिकाओं A तथा C के बीच के विभवांतर, तथा (d) पट्टिका C के पदार्थ की प्रकृति के साथ परिवर्तन के अध्ययन के लिए कर सकते हैं| उत्सर्जक C पर पड़ने वाले प्रकाश के मार्ग में उपयुक्त फिल्टर अथवा रंगीन काँच रखकर भिन्न तरंगदैर्घ्य के प्रकाश का उपयोग कर सकते हैं| प्रकाश स्रोत की उत्सर्जक से दूरी को बदलते हुए प्रकाश की तीव्रता को परिवर्तित किया जा सकता है|
11.4.1 प्रकाश-विद्युत धारा पर प्रकाश की तीव्रता का प्रभाव
संग्राहक A को उत्सर्जक C की तुलना में एक धन विभव पर रखा जाता है जिससे C से उत्सर्जित इलेक्ट्रॉन संग्राहक A की ओर आकर्षित होते हैं| आपतित विकिरण की आवृत्ति तथा विभव को स्थिर रखते हुए, प्रकाश की तीव्रता को परिवर्तित किया जाता है और परिणामी प्रकाश-विद्युत धारा को प्रत्येक बार मापा जाता है| यह पाया जाता है कि प्रकाशिक धारा आपतित प्रकाश की तीव्रता के साथ रैखिकतः बढ़ती है जैसा कि चित्र 11.2 में ग्राफीय रूप में दर्शाया गया है| प्रकाशिक धारा उत्सर्जित होने वाले प्रति सेकंड इलेक्ट्रॉनों की संख्या के अनुक्रमानुपाती है, अतः उत्सर्जित होने वाले प्रति सेकंड प्रकाशिक इलेक्ट्रॉनों की संख्या आपतित विकिरण की तीव्रता के समानुपाती है|
11.4.2 प्रकाश-विद्युत धारा पर विभव का प्रभाव
हम पहले पट्टिका A को पट्टिका C की तुलना में किसी धन विभव पर रखते हैं और पट्टिका C को निश्चित आवृत्ति ν तथा निश्चित तीव्रता I1 के प्रकाश से प्रदीप्त करते हैं| फिर हम पट्टिका A के धन विभव को धीरे-धीरे परिवर्तित करते हैं और प्रत्येक बार परिणामी प्रकाश-विद्युत धारा को मापते हैं| यह पाया जाता है कि प्रकाश-विद्युत धारा धन (त्वरक) विभव के साथ बढ़ती है| पट्टिका A के एक निश्चित धन विभव के लिए एक एेसी स्थिति आ जाती है जिस पर सभी उत्सर्जित इलेक्ट्रॉन पट्टिका A पर संग्रहीत हो जाते हैं तथा प्रकाश-विद्युत धारा उच्चतम हो जाती है अर्थात संतृप्त हो जाती है| यदि हम विद्युत पट्टिका A के त्वरक विभव को और अधिक बढ़ाते हैं तो प्रकाश-विद्युत धारा नहीं बढ़ती| प्रकाश-विद्युत धारा के इस उच्चतम मान को संतृप्त धारा कहते हैं| संतृप्त धारा उस स्थिति के संगत है जब उत्सर्जक पट्टिका C के द्वारा उत्सर्जित सभी प्रकाशिक इलेक्ट्रॉन संग्राहक पट्टिका A पर पहुँच जाते हैं|
चित्र 11.3 आपतित विकिरण की विभिन्न तीव्रताओं के लिए प्रकाशिक-धारा तथा पट्टिका विभव के बीच आलेख|
अब हम पट्टिका A पर पट्टिका C की तुलना में एक ऋण (मंदक) विभव लगाते हैं और इसे धीरे-धीरे अधिक ऋणात्मक करते जाते हैं| जब पट्टिकाओं की ध्रुवता बदली जाती है तो इलेक्ट्रॉन प्रतिकर्षित होते हैं तथा केवल कुछ पर्याप्त ऊर्जा वाले इलेक्ट्रॉन ही संग्राहक A तक पहुँच पाते हैं| यह पाया गया कि प्रकाशिक-धारा तेज़ी से कम होती जाती है जब तक कि यह पट्टिका A पर ऋण विभव V0 के किसी निश्चित तीक्ष्ण और स्पष्ट क्रांतिक मान पर शून्य नहीं हो जाती| आपतित विकिरण की एक निश्चित आवृत्ति के लिए पट्टिका A पर दिया गया निम्नतम ऋण (मंदक) विभव V0 जिस पर प्रकाशिक-धारा शून्य हो जाती है, अंतक (Cut-off)अथवा निरोधी विभव (Stopping potential) कहलाता है|
प्रकाशिक इलेक्ट्रॉन के द्वारा प्रेक्षण की व्याख्या सीधी है| धातु से उत्सर्जित सभी प्रकाशिक इलेक्ट्रॉन समान ऊर्जा वाले नहीं होते| प्रकाश-विद्युत धारा तब शून्य होती है जब निरोधी विभव अधिकतम ऊर्जा वाले प्रकाशिक इलेक्ट्रॉनों, जिनकी उच्चतम गतिज ऊर्जा (Kउच्च) है, को प्रतिकर्षित करने की अवस्था में हो| अर्थात
Kउच्च = e V0 (11.1)
अब हम इस प्रयोग को आपतित विकिरण की एकसमान आवृत्ति परंतु उच्च तीव्रता I2 तथा I3 (I3 > I2 > I1) के लिए दोहरा सकते हैं| हम यह नोट करते हैं कि अब संतृप्त धाराओं के मान बढ़ जाते हैं| इससे ज्ञात होता है कि आपतित विकिरण की तीव्रता के अनुपात में प्रति सेकंड अधिक इलेक्ट्रॉन उत्सर्जित होते हैं| परंतु निरोधी विभव उतना ही रहता है जितना कि I1 तीव्रता के आपतित विकिरण के लिए होता है, जैसा कि चित्र 11.3 में ग्राफ के द्वारा दर्शाया गया है| इस प्रकार, आपतित विकिरण की एक निश्चित आवृत्ति के लिए निरोधी विभव इसकी तीव्रता से स्वतंत्र होता है| दूसरे शब्दों में, प्रकाशिक इलेक्ट्रॉन की उच्चतम गतिज ऊर्जा, आपतित विकिरण की तीव्रता पर निर्भर नहीं करती है|
11.4.3 निरोधी विभव पर आपतित विकिरण की आवृत्ति का प्रभाव
अब हम आपतित विकिरण की आवृत्ति ν और निरोधी विभव V0 के मध्य संबंध का अध्ययन करेंगे| हम प्रकाश विकिरण की विभिन्न आवृत्तियों पर उपयुक्त प्रकार से एक ही तीव्रता को समायोजित करते हैं और संग्राही पट्टिका विभव के साथ प्रकाश-विद्युत धारा के परिवर्तन का अध्ययन करते हैं| परिणामी परिवर्तन को चित्र 11.4 में दर्शाया गया है| हमें आपतित विकिरण की भिन्न आवृत्तियों के लिए निरोधी विभव के भिन्न मान परंतु संतृप्त धारा का एक ही मान प्राप्त होता है| उत्सर्जित इलेक्ट्रॉनों की ऊर्जा आपतित विकिरणों की आवृत्ति पर निर्भर है| आपतित विकिरण की उच्चतर आवृत्ति के लिए निरोधी विभव का मान अधिक ऋणात्मक होता है| चित्र 11.4 से यह ज्ञात होता है कि यदि आवृत्तियाँ ν3 > ν2 > ν1 के क्रम में हों तो निरोधी विभवों का क्रम V03 > V02 > V01 होता है| इसमें यह अंतर्निहित है कि आपतित प्रकाश की आवृत्ति जितनी अधिक होगी, प्रकाशिक इलेक्ट्रॉनों की उच्चतम गतिज ऊर्जा उतनी ही अधिक होगी| फलस्वरूप, इन्हें पूर्ण रूप से रोकने के लिए अधिक निरोधी विभव की आवश्यकता होगी| यदि हम भिन्न धातुओं के लिए आपतित विकिरण की आवृत्ति और संबंधित निरोधी विभव के बीच ग्राफ़ खीचें तो हमें एक सीधी रेखा प्राप्त होती है जैसा कि चित्र 11.5 में दर्शाया गया है|
चित्र 11.4 आपतित विकिरण की विभिन्न आवृत्तियों के लिए पट्टिका विभव तथा प्रकाश-विद्युत धारा के बीच आलेख|
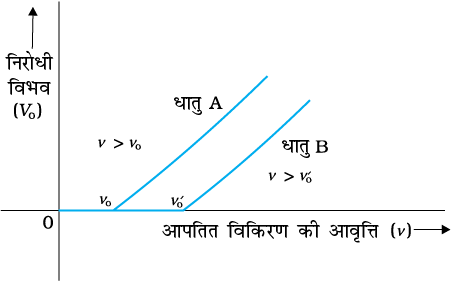
चित्र 11.5 एक दिए हुए प्रकाश संवेदी पदार्थ के लिए आपतित विकिरण की आवृत्ति ν के साथ निरोधी विभव V0 का परिवर्तन|
ग्राफ़ यह दर्शाता है कि
(i) निरोधी विभव V0 एक दिए हुए प्रकाश-संवेदी पदार्थ के लिए, आपतित विकिरण की आवृत्ति के साथ रैखिकतः परिवर्तित होता है|
(ii) एक निश्चित निम्नतम अंतक आवृत्ति ν0 होती है जिसके लिए निरोधी विभव शून्य होता है|
इन प्रेक्षणों में दो तथ्य अंतर्निहित हैं ः
(i) प्रकाशिक इलेक्ट्रॉनों की उच्चतम गतिज ऊर्जा आपतित विकिरण की आवृत्ति के साथ रैखिकतः परिवर्तित होती है जबकि यह इसकी तीव्रता पर निर्भर नहीं होती|
(ii) आपतित विकिरण की आवृत्ति ν के लिए, जबकि इसका मान अंतक आवृत्ति ν0 से कम है, कोई प्रकाश-विद्युत उत्सर्जन संभव नहीं है (तीव्रता अधिक होने की स्थिति में भी)|
इस न्यूनतम अंतक आवृत्ति ν0 को देहली आवृत्ति कहते हैं| यह भिन्न धातुओं के लिए भिन्न होती है|
भिन्न प्रकाश-संवेदी पदार्थ प्रकाश के लिए विभिन्न अनुक्रियाएँ दर्शाते हैं| सेलिनियम, जिंक अथवा कॉपर की तुलना में अधिक संवेदी है| एक ही प्रकाश-संवेदी पदार्थ विभिन्न तरंगदैर्घ्य के प्रकाश के लिए भिन्न अनुक्रिया दर्शाता है| उदाहरण के लिए, कॉपर में पराबैंगनी प्रकाश से प्रकाश-विद्युत प्रभाव होता है जबकि हरे अथवा लाल रंग के प्रकाश से यह प्रभाव नहीं होता|
ध्यान दें कि ऊपर के सभी प्रयोगों में यह पाया गया है कि यदि आपतित विकिरण की आवृत्ति देहली आवृत्ति से अधिक हो जाती है तो बिना किसी काल-पश्चता के तत्काल प्रकाश-विद्युत उत्सर्जन प्रारंभ हो जाता है, तब भी जब आपतित विकिरण बहुत मंद हो| अब यह ज्ञात है कि
10–9s की कोटि के या इससे कम समय में उत्सर्जन प्रारंभ हो जाता है|
अब हम इस अनुभाग में वर्णन किए गए प्रायोगिक लक्षणों एवं प्रेक्षणों का यहाँ सारांश देंगे ः
(i) किसी दिए गए प्रकाश-संवेदी पदार्थ और आपतित विकिरण की आवृत्ति (देहली आवृत्ति से अधिक) के लिए, प्रकाश-विद्युत धारा आपतित प्रकाश की तीव्रता के अनुक्रमानुपाती होती है (चित्र 11.2)|
(ii) किसी दिए गए प्रकाश-संवेदी पदार्थ और आपतित विकिरण की आवृत्ति के लिए, संतृप्त धारा आपतित विकिरण की तीव्रता के अनुक्रमानुपाती पाई जाती है जबकि निरोधी विभव तीव्रता पर निर्भर नहीं होता है (चित्र 11.3)|
(iii) किसी दिए गए प्रकाश-संवेदी पदार्थ के लिए, एक निश्चित न्यूनतम अंतक-आवृत्ति होती है जिसे देहली आवृत्ति कहते हैं, जिसके नीचे प्रकाशिक इलेक्ट्रॉनों का कोई उत्सर्जन नहीं होता चाहे आपतित प्रकाश कितना भी तीव्र क्यों न हो| देहली आवृत्ति के ऊपर, निरोधी विभव अथवा तुल्यतः उत्सर्जित प्रकाशिक इलेक्ट्रॉनों की उच्चतम गतिज ऊर्जा आपतित विकिरण की आवृत्ति के साथ रैखिकतः बढ़ती है परंतु यह इसकी तीव्रता से स्वतंत्र होती है (चित्र 11.5)|
(iv) प्रकाश-विद्युत उत्सर्जन बिना किसी काल-पश्चता के (∼10–9s अथवा कम) एक तात्क्षणिक प्रक्रिया है, तब भी जब आपतित विकिरण को अत्यधिक मंद कर दिया जाता है|
11.5 प्रकाश-विद्युत प्रभाव तथा प्रकाश का तरंग सिद्धांत
प्रकाश की तरंग प्रकृति उन्नीसवीं शताब्दी के अंत तक अच्छी तरह स्थापित हो गई थी| प्रकाश के तरंग-चित्र के द्वारा व्यतिकरण, विवर्तन तथा ध्रुवण की घटनाओं की स्वाभाविक एवं संतोषजनक रूप में व्याख्या की जा चुकी थी| इस चित्र के अनुसार, प्रकाश एक वैद्युतचुंबकीय तरंग है, जो विद्युत एवं चुंबकीय क्षेत्र से मिलकर बनी होती है तथा जिस आकाशीय क्षेत्र में फैली होती है, वहाँ ऊर्जा का संतत वितरण होता है| अब हम यह देखेंगे कि क्या प्रकाश का यह तरंग-चित्रण पिछले अनुभाग में दिए गए प्रकाश-विद्युत उत्सर्जन संबंधी प्रेक्षणों की व्याख्या कर सकता है|
प्रकाश-विद्युत उत्सर्जन के तरंग-चित्रण के अनुसार धातु के पृष्ठ (जहाँ विकिरण की किरण-पुंज पड़ती है) पर स्वतंत्र इलेक्ट्रॉन विकिरित ऊर्जा को संतत रूप में अवशोषित करते हैं| जितनी अधिक प्रकाश की तीव्रता होगी उतने ही अधिक वैद्युत तथा चुंबकीय क्षेत्रों के आयाम होंगे| परिणामस्वरूप, तीव्रता जितनी अधिक होगी उतना ही अधिक प्रत्येक इलेक्ट्रॉन के द्वारा ऊर्जा-अवशोषण होना चाहिए| इस चित्रण के अनुसार, प्रकाशिक इलेक्ट्रॉन की उच्चतम गतिज ऊर्जा तीव्रता में वृद्धि के साथ बढ़नी चाहिए| साथ ही, चाहे प्रकाश की आवृत्ति कुछ भी हो, एक पर्याप्त तीव्र विकिरण किरण-पुंज (पर्याप्त समय में) इलेक्ट्रॉनों को इतनी पर्याप्त ऊर्जा देने में समर्थ होगा जो इनके धातु-पृष्ठ से बाहर निकलने के लिए आवश्यक निम्नतम ऊर्जा से अधिक होगी| इसलिए, एक देहली आवृत्ति का अस्तित्व नहीं होना चाहिए| तरंग सिद्धांत की इन प्रागुक्तियों से अनुभाग 11.4.3 में दिए गए प्रेक्षणों (i), (ii) तथा (iii) का सीधे विरोध होता है|
आगे हमें ध्यान रखना होगा कि तरंग-चित्रण में, इलेक्ट्रॉन द्वारा ऊर्जा का संतत अवशोषण विकिरण के पूरे तरंगाग्र पर होता है| चूँकि एक बड़ी संख्या में इलेक्ट्रॉन ऊर्जा अवशोषित करते हैं, अतः प्रति इलेक्ट्रॉन प्रति इकाई समय में अवशोषित ऊर्जा बहुत कम होगी| स्पष्ट गणना से यह आकलन किया जा सकता है कि एकल इलेक्ट्रॉन के लिए कार्य-फलन को पार कर धातु से बाहर निकल आने के लिए पर्याप्त ऊर्जा जुटाने में कई घंटे अथवा और भी अधिक समय लग सकता है| यह निष्कर्ष भी प्रेक्षण (iv), जिसके अनुसार प्रकाश-विद्युत उत्सर्जन (लगभग) तात्क्षणिक होता है, के बिलकुल विपरीत है| संक्षेप में, तरंग-चित्रण के द्वारा प्रकाश-विद्युत उत्सर्जन के अत्यंत मूल लक्षणों की व्याख्या नहीं हो सकती|
11.6 आइंस्टाइन का प्रकाश-विद्युत समीकरण ः विकिरण का ऊर्जा क्वांटम
सन्् 1905 में अल्बर्ट आइंसटाइन (1879 – 1955) ने प्रकाश-विद्युत प्रभाव की व्याख्या के लिए वैद्युतचुंबकीय विकिरण का एक मौलिक रूप से नया चित्रण प्रस्तावित किया| इस चित्रण में, प्रकाश-विद्युत उत्सर्जन विकिरण से संतत ऊर्जा-अवशोषण के द्वारा नहीं होता| विकिरण ऊर्जा विविक्त इकाइयों से बनी होती है–जो विकिरण की ऊर्जा के क्वांटा कहलाते हैं| विकिरण ऊर्जा के प्रत्येक क्वांटम की ऊर्जा hν होती है, जहाँ h प्लांक स्थिरांक है और ν प्रकाश की आवृत्ति| प्रकाश-विद्युत प्रभाव में, एक इलेक्ट्रॉन विकिरण के एक क्वांटम की ऊर्जा (hν) अवशोषित करता है| यदि ऊर्जा का यह अवशोषित क्वांटम इलेक्ट्रॉन के लिए धातु की सतह से बाहर निकल आने के लिए निम्नतम आवश्यक ऊर्जा से अधिक होता है (कार्य-फलन, φ0) तब उत्सर्जित इलेक्ट्रॉन की अधिकतम गतिज ऊर्जा होगी :
Kउच्च = hν – φ0 (11.2)
अल्बर्ट आइंस्टाइन (1879 – 1955)
अल्बर्ट आइंस्टाइन (1879 – 1955) सन् 1879 में जर्मनी में उल्म नामक स्थान पर जन्मे अल्बर्ट आइंसटाइन आज तक के विश्व के भौतिकविदों में सर्वाधिक महान भौतिकविद के रूप में जाने जाते हैं| उनका विस्मयकारी वैज्ञानिक जीवन उनके सन् 1905 में प्रकाशित तीन क्रांतिकारी शोधपत्रों से आरंभ हुआ| उन्होंने अपने प्रथम शोधपत्र में प्रकाश क्वांटा (अब फ़ोटॉन कहा जाता है) की धारणा को प्रस्तुत किया और प्रकाश-वैद्युत प्रभाव के उस लक्षण की व्याख्या की जिसे विकिरण का चिरप्रतिष्ठित तरंग सिद्धांत नहीं समझा सका| अपने दूसरे शोधपत्र में उन्होंने ब्राउनी गति का सिद्धांत विकसित किया जिसकी कुछ वर्षों बाद प्रयोगात्मक पुष्टि हुई और जिसने द्रव्य के आण्विक चित्रण का विश्वासोत्पादक साक्ष्य उपलब्ध कराया| उनके तृतीय शोधपत्र ने आपेक्षिकता के विशिष्ट सिद्धांत को जन्म दिया| सन् 1916 में उन्होंने आपेक्षिकता के व्यापक सिद्धांत को प्रकाशित किया| आइंस्टाइन के कुछ अन्य महत्वपूर्ण योगदान हैं : उद्दीपित उत्सर्जन की धारणा जो प्लांक कृष्णिका विकिरण नियम के एक वैकल्पिक व्युत्पन्न में प्रस्तुत की गई है, विश्व का स्थैतिक प्रतिरूप जिसने आधुनिक ब्रह्मांडिकी का आरंभ किया, किसी गैस के स्थूल बोसॉन की क्वांटम-सांख्यिकी तथा क्वांटम-यांत्रिकी की संस्थापना का आलोचनात्मक विश्लेषण| सैद्धांतिक भौतिकी में उनके योगदान तथा प्रकाश-विद्युत प्रभाव के लिए 1921 में उन्हें नोबेल पुरस्कार से सम्मानित किया गया|
समीकरण (11.2) को आइंस्टाइन का प्रकाश-विद्युत समीकरण कहते हैं| अब हम यह देख सकते हैं कि किस प्रकार यह समीकरण अनुभाग 11.4.3 में दिए प्रकाश-विद्युत प्रभाव से संबंधित सभी प्रेक्षणों को एक सरल एवं परिष्कृत ढंग से प्रस्तुत करता है|
• समीकरण (11.2) के अनुसार, प्रेक्षण के अनुरूप, Kउच्च आवृत्ति ν पर रैखिकतः निर्भर करती है और विकिरण की तीव्रता पर निर्भर नहीं करती है| एेसा इसलिए हुआ है क्योंकि आइंस्टाइन के चित्रण में, प्रकाश-विद्युत प्रभाव एकल इलेक्ट्रॉन द्वारा विकिरण के एकल क्वांटम के अवशोषण से उत्पन्न होता है| विकिरण की तीव्रता (जो ऊर्जा क्वांटमों की संख्या प्रति इकाई क्षेत्रफल प्रति इकाई समय के अनुक्रमानुपाती है) इस मूल प्रक्रिया के लिए असंगत है|
• क्योंकि Kउच्च ऋण राशि नहीं होगी, समीकरण (11.2) में यह अंतर्निहित है कि प्रकाश-विद्युत उत्सर्जन तभी संभव है जब
h ν > φ0
अथवा ν > ν0 , जहाँ
ν0 =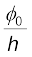 
(11.3)
समीकरण (11.3) के अनुसार, कार्य-फलन φ0 के अधिक मान के लिए, प्रकाशिक इलेक्ट्रॉन उत्सर्जित करने के लिए आवश्यक न्यूनतम अथवा देहली आवृत्ति ν0 का मान अधिक होगा| इस प्रकार, एक देहली आवृत्ति ν0 (= φ0/h) अस्तित्व में होती है जिससे कम आवृत्ति पर कोई प्रकाश-विद्युत उत्सर्जन संभव नहीं है, चाहे विकिरण की तीव्रता कुछ भी क्यों न हो अथवा वह पृष्ठ पर कितनी भी देर क्यों न पड़े|
• इस चित्रण में, विकिरण की तीव्रता, जैसा ऊपर परिलक्षित है, ऊर्जा क्वांटा की संख्या प्रति इकाई क्षेत्रफल प्रति इकाई समय के अनुक्रमानुपाती होती है| जितनी अधिक संख्या में ऊर्जा क्वांटा उपलब्ध होंगे, उतनी ही अधिक संख्या में इलेक्ट्रॉन ऊर्जा क्वांटा का अवशोषण करेंगे और इसलिए (ν > ν0 के लिए) धातु से बाहर आने वाले इलेक्ट्रॉनों की संख्या उतनी ही अधिक होगी| इससे यह स्पष्ट हो जाता है कि क्यों ν > ν0 के लिए प्रकाश-विद्युत धारा तीव्रता के अनुक्रमानुपाती होती है|
• आइंस्टाइन के चित्रण में, प्रकाश-विद्युत प्रभाव में एक इलेक्ट्रॉन के द्वारा प्रकाश के एक क्वांटम का अवशोषण मूल प्राथमिक प्रक्रिया होती है| यह प्रक्रिया तात्क्षणिक होती है| इस प्रकार, तीव्रता अर्थात विकिरण क्वांटा की संख्या चाहे जितनी भी हो, प्रकाश-विद्युत उत्सर्जन तात्क्षणिक ही होगा| कम तीव्रता से उत्सर्जन में विलंब नहीं होगा क्योंकि मूल प्राथमिक प्रक्रिया वही रहेगी| तीव्रता से केवल यह निर्धारित होता है कि कितने इलेक्ट्रॉन इस प्राथमिक प्रक्रिया (एक एकल इलेक्ट्रॉन द्वारा एक प्रकाश क्वांटम का अवशोषण) में भाग ले सकने वाले इलेक्ट्रॉनों की संख्या से ही प्रकाश-विद्युत धारा के परिमाण का निर्धारण होता है|
समीकरण (11.1) का उपयोग कर, प्रकाश-विद्युत समीकरण (11.2) को इस प्रकार लिखा जा सकता है
e V0 = h ν – φ0 ; के लिए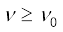 
अथवा V0 =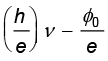 
(11.4)
यह एक महत्वपूर्ण परिणाम है| इससे यह प्रागुक्ति होती है कि V0 के विरुद्ध ν का वक्र एक सरल रेखा है, जिसका ढलान = (h/e), जो कि पदार्थ की प्रकृति पर निर्भर नहीं करता| 1906-1916 के मध्य, मिलिकन ने आइंस्टाइन के प्रकाश-विद्युत समीकरण को असत्यापित करने के लिए प्रकाश-वैद्युत प्रभाव पर प्रयोगों की शृंखला की| चित्र 11.5 में दर्शाए अनुसार, उसने सोडियम के लिए प्राप्त सरल रेखा का ढलान मापा| e के ज्ञात मान का उपयोग कर उसने प्लांक स्थिरांक h का मान निर्धारित किया था| यह मान प्लांक स्थिरांक के उस मान (= 6.626 × 10–34J s) के निकट था जिसे बिलकुल ही भिन्न संदर्भ में ज्ञात किया गया था| इस प्रकार से 1916 में मिलिकन ने आइंस्टाइन के प्रकाश-विद्युत समीकरण को असत्यापित करने के स्थान पर उसकी सत्यता को स्थापित किया|
प्रकाश क्वांटा की परिकल्पना एवं h तथा φ0 के मान (जो अन्य प्रयोगों से प्राप्त मान से मेल रखते हैं) के निर्धारण के उपयोग से प्रकाश-विद्युत प्रभाव के आइंस्टाइन के चित्रण को स्वीकारा गया| मिलिकन ने प्रकाश-विद्युत समीकरण को बड़ी परिशुद्धता से कई क्षारीय धातुओं के लिए विकिरण-आवृत्तियों के विस्तृत परास के लिए सत्यापित किया|
11.7 प्रकाश की कणीय प्रकृति : फ़ोटॉन
प्रकाश-विद्युत प्रभाव ने इस विलक्षण तथ्य को प्रमाणित किया कि प्रकाश किसी द्रव्य के साथ अन्योन्य क्रिया में इस प्रकार व्यवहार करता है जैसे यह क्वांटा अथवा ऊर्जा के पैकेट (जिनमें प्रत्येक की ऊर्जा h ν है) का बना हो|
क्या प्रकाश ऊर्जा के क्वांटम को किसी कण से संबद्ध किया जा सकता है? आइंसटाइन एक महत्वपूर्ण परिणाम पर पहुँचे कि प्रकाश क्वांटम को संवेग (h ν/c) से संबद्ध किया जा सकता है| ऊर्जा के साथ-साथ संवेग का निश्चित मान इसका प्रबल सूचक है कि प्रकाश क्वांटम को कण से संबद्ध किया जा सकता है| इस कण को बाद में फ़ोटॉन नाम दिया गया| प्रकाश के कण जैसे व्यवहार को ए. एच. कांपटन (1892-1962) के इलेक्ट्रॉन के द्वारा X-किरणों के प्रकीर्णन के प्रयोग से सन् 1924 में पुनः पुष्ट किया गया| सैद्धांतिक भौतिकी में योगदान तथा प्रकाश-विद्युत प्रभाव के अपने कार्य के लिए आइंस्टाइन को 1921 में भौतिकी का नोबेल पुरस्कार प्रदान किया गया| विद्युत के मूल आवेश तथा प्रकाश-विद्युत प्रभाव पर किए गए कार्य के लिए सन् 1923 में मिलिकन को भौतिकी का नोबेल पुरस्कार प्रदान किया गया|
हम वैद्युतचुंबकीय विकिरण के फ़ोटॉन चित्रण का सारांश निम्नानुसार दे सकते हैं :
(i) विकिरण के द्रव्य के साथ अन्योन्य क्रिया में, विकिरण इस प्रकार व्यवहार करता है मानो यह एेसे कणों से बना हो जिन्हें फ़ोटॉन कहते हैं|
(ii) प्रत्येक फ़ोटॉन की ऊर्जा E (=hν) होती है और संवेग p (= h ν/c) तथा चाल c होती है| जहाँ c प्रकाश की चाल है|
(iii) एक निश्चित आवृत्ति ν, अथवा तरंगदैर्घ्य λ, के सभी फ़ोटॉनों की ऊर्जा E (=hν = hc/λ) और संवेग p (= hν/c= h/λ), एकसमान होते हैं (विकिरण की तीव्रता चाहे जो भी हो)| किसी दी गई तरंगदैर्घ्य के प्रकाश की तीव्रता बढ़ाने पर केवल किसी दिए गए क्षेत्र से गुज़रने वाले प्रति सेकंड फोटॉनों की संख्या ही बढ़ती है (सभी फोटॉनों की ऊर्जा एकसमान होती है)| अतः फ़ोटॉन की ऊर्जा विकिरण की तीव्रता पर निर्भर नहीं करती|
(iv) फ़ोटॉन विद्युत उदासीन होते हैं और विद्युत तथा चुंबकीय क्षेत्रों के द्वारा विक्षेपित नहीं होते|
(v) फ़ोटॉन-कण संघट्ट (जैसे कि फोटॉन-इलेक्ट्रॉन संघट्ट) में कुल ऊर्जा तथा कुल संवेग संरक्षित रहते हैं| तथापि, किसी संघट्ट में फ़ोटॉनों की संख्या भी संरक्षित नहीं रह सकती है| फ़ोटॉन अवशोषित हो सकता है अथवा एक नया फ़ोटॉन सृजित हो सकता है|
उदाहरण 11.1 6.0 ×1014 Hz आवृत्ति का एकवर्णी प्रकाश किसी लेसर के द्वारा उत्पन्न किया जाता है| उत्सर्जन क्षमता 2.0 ×10–3 W है| (a) प्रकाश किरण-पुंज में किसी फ़ोटॉन की ऊर्जा कितनी है? (b) स्रोत के द्वारा औसत तौर पर प्रति सेकंड कितने फ़ोटॉन उत्सर्जित होते हैं?
हल
(a)प्रत्येक फ़ोटॉन की ऊर्जा होगी
E = h ν = ( 6.63 ×10–34 J s) (6.0 ×1014 Hz)
= 3.98 × 10–19 J
(b)यदि स्रोत के द्वारा प्रति सेकंड उत्सर्जित फ़ोटॉनों की संख्या N है तो किरण-पुंज में संचरित क्षमता P प्रति फ़ोटॉन ऊर्जा E के N गुना होगी जिससे कि P = N E | तब
N =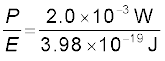 
= 5.0 ×1015 फ़ोटॉन प्रति सेकंड
उदाहरण 11.2 यदि सीज़ियम का कार्य-फलन 2.14 eV है तो परिकलन कीजिए :
(a) सीज़ियम की देहली आवृत्ति तथा (b) आपतित प्रकाश का तरंगदैर्घ्य, यदि प्रकाशिक धारा को 0.60 V का एक निरोधी विभव लगाकर शून्य किया जाए|
हल
(a)अंतक अथवा देहली आवृत्ति के लिए, आपतित विकिरण की ऊर्जा h ν0 कार्य फलन φ0 के समान होती है| अतः
ν0 =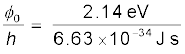 
इस प्रकार ν0 = 5.16 × 1014 Hz से कम आवृत्तियों के लिए, कोई प्रकाशिक इलेक्ट्रॉन मुक्त नहीं होता है|
(b)उत्सर्जित प्रकाशिक इलेक्ट्रॉनों की उच्चतम गतिज ऊर्जा e V0 स्थितिज ऊर्जा (मंदन-विभव V0 के द्वारा) के समान होने की स्थिति में प्रकाशिक धारा शून्य हो जाती है| आइंस्टाइन का प्रकाश-विद्युत समीकरण निम्न है :
eV0 = hν – φ0 =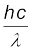 
– φ0
अथवा λ = hc/(eVo + φ0)
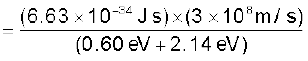
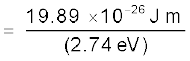
उदाहरण 11.3 दृश्य क्षेत्र में बैंगनी रंग, पीले-हरे रंग तथा लाल रंग के प्रकाश की तरंगदैर्घ्य क्रमशः लगभग 390 nm, लगभग 550 nm (औसत तरंगदैर्घ्य) तथा लगभग 760 nm है|
(a) दृश्य क्षेत्र के निम्न प्रकाश के लिए फ़ोटॉन की ऊर्जा (eV) क्या होगीः (i) बैंगनी सिरा;
(ii) पीले-हरे रंग की औसत तरंगदैर्घ्य; तथा (iii) लाल सिरा (h = 6.63×10–34 J s तथा 1 eV = 1.6×10 –19J)
(b) प्रकाश-संवेदी पदार्थों के लिए सारणी 11.1 में दिए गए कार्य-फलनों के मान तथा (a) प्रश्न के (i), (ii) तथा (iii) भागों के परिणामों को उपयोग में लाते हुए क्या आप दृश्य प्रकाश के साथ कार्य कर सकने वाली प्रकाश विद्युत युक्ति का सृजन कर सकते हैं?
हल
(a) आपतित फ़ोटॉन की ऊर्जा E = hν = hc/λ
E = (6.63×10–34J s) (3×108 m/s)/λ
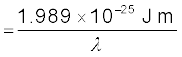
(i) बैंगनी प्रकाश के लिए λ1 = 390 nm (निम्न तरंगदैर्घ्य सिरा)
आपतित फ़ोटॉन ऊर्जा, E1 =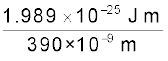 
= 5.10 × 10–19J
=
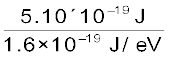
= 3.19 eV
(ii) पीले-हरे प्रकाश के लिए, λ2 = 550 nm (औसत तरंगदैर्घ्य)
आपतित फ़ोटॉन ऊर्जा, E2 =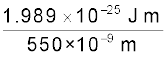 
= 3.62×10–19 J = 2.26 eV
(iii) लाल प्रकाश के लिए, λ3 = 760 nm (उच्च तरंगदैर्घ्य सिरा)
आपतित फ़ोटॉन ऊर्जा, E3 =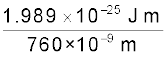 
= 2.62×10–19 J = 1.64 eV
(b) किसी प्रकाश-विद्युत युक्ति के कार्य के लिए आपतित प्रकाश ऊर्जा E का मान प्रयुक्त पदार्थ के कार्य-फलन के मान के समान या अधिक होना चाहिए| अतः बैंगनी प्रकाश (E = 3.19 eV) के लिए कार्य कर सकने वाली प्रकाश-विद्युत युक्ति के प्रकाश-संवेदी पदार्थ, Na (कार्य फलन φ0 = 2.75 eV), K (कार्य-फलन φ0 = 2.30 eV) तथा Cs(कार्य-फलन φ0 = 2.14 eV) हो सकते हैं| यह युक्ति पीले-हरे प्रकाश (E = 2.26 eV) के लिए प्रकाश-संवेदी पदार्थCs (कार्य-फलन φ0 = 2.14 eV), के उपयोग से ही कार्य कर सकती है| तथापि, यह युक्ति लाल प्रकाश (E = 1.64eV) के लिए उपरोक्त तीनों में से किसी प्रकाश-संवेदी पदार्थ के उपयोग से कार्य नहीं कर सकेगी|
11.8 द्रव्य की तरंग प्रकृति
प्रकाश (व्यापक तौर पर वैद्युतचुंबकीय विकिरण) की द्वैत प्रकृति (तरंग-कण), वर्तमान तथा पूर्व अध्यायों में किए गए अध्ययन द्वारा, स्पष्ट रूप से प्रकट होती है| प्रकाश की तरंग प्रकृति व्यतिकरण, विवर्तन तथा ध्रुवण की परिघटनाओं में दृष्टिगोचर होती है| दूसरी ओर, प्रकाश-विद्युत प्रभाव तथा कॉम्पटन प्रभाव जिनमें ऊर्जा और संवेग का अंतरण होता है, विकिरण इस प्रकार व्यवहार करता है कि मानो यह कणों के गुच्छ अर्थात फ़ोटॉनों से बना हो| कण अथवा तरंग-चित्रण में से कौन किसी प्रयोग को समझने में सर्वाधिक उपयुक्त है, यह प्रयोग की प्रकृति पर निर्भर है| उदाहरण के लिए, अपने नेत्रों से किसी वस्तु को देखने की सुपरिचित घटना में दोनों ही चित्रण महत्वपूर्ण हैं| नेत्र लेंस द्वारा प्रकाश को एकत्र कर फ़ोकस करने की प्रक्रिया को तरंग-चित्रण से भली-भाँति विवेचित किया गया है| परंतु इसका शलाकाओं तथा शंकुओं (रेटिना के) द्वारा अवशोषण में फोटॉन चित्रण की आवश्यकता होती है|
एक स्वाभाविक प्रश्न यह उठता है कि यदि विकिरण की द्वैत प्रकृति (तरंग तथा कण) है तो क्या प्रकृति के कण (इलेक्ट्रॉन, प्रोटॉन आदि) भी तरंग-जैसा लक्षण प्रदर्शित करते हैं? सन् 1924 में एक फ्रांसीसी भौतिकवैज्ञानिक लुइस विक्टर दे ब्रॉग्ली (फ्रेंच उच्चारण में इसे लुई विक्टर दे ब्राए पुकारा जाता है) (1892 – 1987) ने एक निर्भीक परिकल्पना को प्रस्तुत किया कि पदार्थ के गतिमान कण उपयुक्त परिस्थितियों में तरंग सदृश गुण प्रदर्शित कर सकते हैं| उसने यह तर्क दिया कि प्रकृति सममित है और दो मूल भौतिक सत्ताओं, द्रव्य एवं ऊर्जा, का भी सममित लक्षण होना चाहिए| यदि विकिरण का द्वैत लक्षण है तो द्रव्य का भी होना चाहिए| दे ब्रॉग्ली ने प्रस्तावित किया कि संवेग p के कण के साथ जुड़ी तरंगदैर्घ्य λ निम्न प्रकार दर्शायी जा सकती है ः
λ =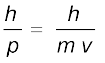 
(11.5)
जहाँ m कण का द्रव्यमान तथा v इसकी चाल है| समीकरण (11.5) को दे ब्रॉग्ली का संबंध और द्रव्य-तरंग के तरंगदैर्घ्य λ को दे ब्रॉग्ली तरंगदैर्घ्य कहते हैं| द्रव्य का द्वैत स्वरूप दे ब्रॉग्ली के संबंध में स्पष्ट है| समीकरण (11.5) की बाईं ओर, λ तरंग का लक्षण है जबकि दाईं ओर संवेग p कण का विशिष्ट लक्षण है| प्लांक स्थिरांक h दोनों लक्षणों को संयोजित करता है|
समीकरण (11.5) एक पदार्थ-कण के लिए मूलतः एक परिकल्पना है जिसकी तर्कसंगति केवल प्रयोग के द्वारा ही परखी जा सकती है| तथापि, यह देखना रोचक है कि यह एक फ़ोटॉन के द्वारा भी संतुष्ट होता है| एक फ़ोटॉन के लिए, जैसा कि हमने देखा है,
p = hν /c (11.6)
इसलिए,
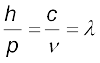(11.7)
अर्थात, एक फोटॉन का दे ब्रॉग्ली तरंगदैर्घ्य जो समीकरण (11.5) द्वारा दिया गया है उस वैद्युतचुंबकीय विकिरण के तरंगदैर्घ्य के समान होता है तथा फोटॉन विकिरण की ऊर्जा तथा संवेग का एक क्वांटम है|
स्पष्टतः समीकरण (11.5) के द्वारा, λ एक ज़्यादा भारी कण (बड़ा m) अथवा अधिक ऊर्जस्वी कण (बड़े v) के लिए छोटा होगा| उदाहरण के लिए, एक 0.12 kg द्रव्यमान की गेंद जो 20 m s–1 की चाल से चल रही है, की दे ब्रॉग्ली तरंगदैर्घ्य का सरलता से परिकलन किया जा सकता है|
p = m v = 0.12 kg × 20 m s–1 = 2.40 kg m s–1
λ =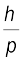 
= 
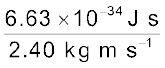= 2.76 × 10–34 m
यह तरंगदैर्घ्य इतनी छोटी है कि यह किसी मापन की सीमा से बाहर है| यही कारण है कि स्थूल वस्तुएँ हमारे दैनिक जीवन में तरंग-सदृश गुण नहीं दर्शातीं| दूसरी ओर, अव-परमाण्विक डोमेन (Sub-atomic domain) में, कणों का तरंग लक्षण महत्वपूर्ण है तथा मापने योग्य है|
फ़ोटो सेल
फ़ोटो सेल (प्रकाश सेल) प्रकाश-विद्युत प्रभाव का एक शिल्प प्रौद्योगिकीय अनुप्रयोग है| यह एक एेसी युक्ति है जो प्रकाश-ऊर्जा को वैद्युत-ऊर्जा में बदल देती है| इसे कभी-कभी विद्युत नेत्र भी कहते हैं| एक फ़ोटो सेल में एक अर्ध-बेलनाकार प्रकाश-संवेदी धातु पट्टिका C (उत्सर्जक) होती है और एक तार का पाश (लूप) A (संग्राहक) एक निर्वातित काँच या क्वार्टज़ बल्ब में लगे होते हैं| इसे चित्र में दर्शाए अनुसार किसी बाह्य परिपथ में एक उच्च-विभव बैटरी B तथा माइक्रोएेमीटर (µ A) के साथ संयोजित किया जाता है, कभी-कभी पट्टिका C के स्थान पर, प्रकाश-संवेदी पदार्थ (c) की एक पतली परत बल्ब की भीतरी सतह पर चिपका दी जाती है| बल्ब के एक भाग को साफ़ छोड़ दिया जाता है जिससे कि प्रकाश इसमें प्रवेश कर सके|
जब उपयुक्त तरंगदैर्घ्य का प्रकाश उत्सर्जक C पर पड़ता है तो इलेक्ट्रॉन उत्सर्जित होते हैं| ये प्रकाशिक इलेक्ट्रॉन संग्राहक पर आकर्षित हो जाते हैं| किसी प्रकाश सेल से कुछ माइक्रोएेम्पियर की कोटि की प्रकाशिक धारा प्राप्त की जाती है|
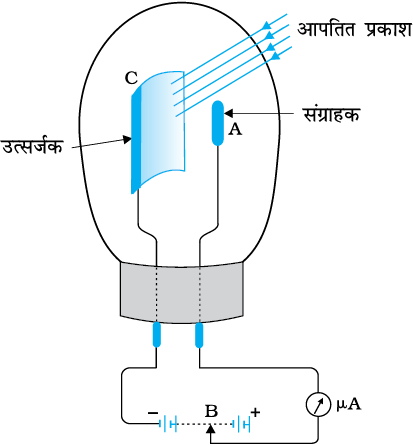
फ़ोटो सेल
एक प्रकाश सेल प्रदीप्त-तीव्रता में परिवर्तन कर प्रकाशिक धारा में परिवर्तन कर सकता है| यह धारा नियंत्रण तंत्र के चालन और प्रकाश मापक युक्तियों में उपयोग में लाई जा सकती है| अवरक्त विकिरण के लिए संवेदी लेड सल्फ़ाइड के प्रकाश सेलों का उपयोग इलेक्ट्रॉनिक प्रज्वलन परिपथों में किया जाता है|
वैज्ञानिक कार्यों में, प्रकाश की तीव्रता को मापने के सभी अनुप्रयोगों में प्रकाश सेलों का उपयोग किया जाता है| फ़ोटोग्राफी कैमरों में प्रकाश मापक प्रकाश सेल का उपयोग आपतित प्रकाश की तीव्रता मापने में करते हैं| स्वचालित द्वार नियंत्रक में प्रकाश सेल का प्रयोग द्वार-प्रकाश विद्युत परिपथ में होता है| द्वार की ओर बढ़ते हुए व्यक्ति द्वारा प्रकाश सेल पर पड़ने वाले प्रकाश पुंज बाधित हो सकते हैं| प्रकाशिक धारा में अचानक होने वाले बदलाव का उपयोग द्वार खोलने के लिए मोटर को प्रारंभ करने में या अलार्म बजाने में किया जा सकता है| इनका उपयोग उस गणना युक्ति के नियंत्रण में भी किया जाता है जो प्रकाश किरण-पुंज की प्रत्येक रुकावट, जो किरण-पुंज के पार किसी व्यक्ति अथवा वस्तु के जाने के कारण उत्पन्न होती है, को अंकित करता है| इसलिए, प्रकाश सेल किसी प्रेक्षागृह में प्रवेश करने वाले व्यक्तियों की गणना करने में सहायता करता है, यदि वे विशाल कक्ष में एक-एक करके प्रवेश करते हों| इनका उपयोग यातायात नियम तोड़ने वालों की पहचान के लिए किया जाता है| जब भी विकिरण के एक किरण-पुंज को अवरोधित किया जाता है तो एक एलार्म बजाया जा सकता है|
चोर एलार्म में, पराबैंगनी प्रकाश (अदृश्य) को संतत प्रवेश-द्वार पर स्थापित प्रकाश सेल पर डाला जाता है| कोई व्यक्ति जो द्वार में प्रवेश करता है वह प्रकाश सेल पर पड़ने वाले किरण-पुंज को अवरोधित करता है| प्रकाशक विद्युत-धारा में आकस्मिक परिवर्तन का उपयोग एक विद्युत घंटी के बजने से प्रारंभ किया जाता है| अग्नि-एलार्म में, भवन में उपयुक्त स्थानों पर कई प्रकाश सेल स्थापित कर दिए जाते हैं| आग लगने पर प्रकाश विकिरण प्रकाश सेल पर पड़ते हैं| इससे एक विद्युत घंटी अथवा एक भोंपू से होकर जाने वाला परिपथ पूर्ण हो जाता है और यह एक चेतावनी-संकेत के रूप में कार्य करना प्रारंभ कर देता है|
प्रकाश सेलों का उपयोग चल चित्रण में ध्वनि के पुनरुत्पादन तथा टेलीविज़न कैमरे में दृश्य के क्रमवीक्षण (scanning) तथा टेलिविज़न प्रसारण (telecasting) में किया जाता है| इनका प्रयोग उद्योगों में धातु की चादरों में छोटी त्रुटियों तथा छिद्रों को खोजने में भी किया जाता है|
एक इलेक्ट्रॉन (द्रव्यमान m, आवेश e) जिसे विरामावस्था से एक विभव V द्वारा त्वरित किया जाता है, का विचार करें| इलेक्ट्रॉन की गतिज ऊर्जा K इस पर विद्युत क्षेत्र द्वारा किए गए कार्य (V e) के बराबर होगी :
K = e V (11.8)
यहाँ K =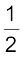 
m v2 = 
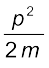, जिससे
p =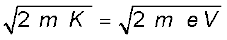 
(11.9)
तब इलेक्ट्रॉन का दे ब्रॉग्ली तरंगदैर्घ्य λ होगा
λ =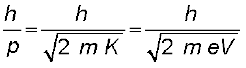 
(11.10)
h, m तथा e के सांख्यिक मान को स्थानापन्न करने पर हम निम्न मान पाते हैं
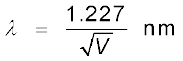(11.11)
जहाँ V त्वरक विभव का वोल्ट में मान है| एक 120 V त्वरक विभव के लिए, समीकरण (11.11) से λ = 0.112 nm प्राप्त होता है| यह तरंगदैर्घ्य उसी कोटि की है जितनी दूरी क्रिस्टलों में परमाण्वीय तलों के बीच होती है| इससे यह संकेत मिलता है कि एक इलेक्ट्रॉन से जुड़ी पदार्थ तरंग को X-किरण विवर्तन जैसे क्रिस्टल विवर्तन प्रयोगों से परखा जा सकता है| हम अगले अनुभाग में दे ब्रॉग्ली की परिकल्पना के प्रायोगिक परीक्षण का वर्णन करेंगे| इलेक्ट्रॉन की तरंगीय प्रकृति की खोज के लिए दे ब्रॉग्ली को 1929 में भौतिकी के नोबेल पुरस्कार से सम्मानित किया गया|
द्रव्य-तरंग चित्रण ने हाइज़नबर्ग के अनिश्चितता सिद्धांत को परिष्कृत रूप में समाविष्ट किया| इस सिद्धांत के अनुसार, एक ही समय पर किसी इलेक्ट्रॉन (अथवा कोई और कण) की स्थिति एवं संवेग दोनों को परिशुद्ध रूप से मापना असंभव है| हमेशा ही कुछ अनिश्चितता (∆x) स्थिति के विनिर्देश और कुछ अनिश्चितता (∆p) संवेग के विनिर्देश में होती है| ∆x तथा ∆p के गुणनफल की एक निम्नतर सीमा होती है, जो ö* (जहाँ ö = h/2π) की कोटि की होती है, अर्थात्
∆x ∆p ≈ ö (11.12)
लुईस विक्टर दे ब्रॉग्ली (1892 – 1987)
लुईस विक्टर दे ब्रॉग्ली (1892 – 1987) फ्रांसीसी भौतिकविद, जिन्होंने द्रव्य की तरंग प्रकृति का क्रांतिकारी विचार प्रस्तुत किया| यह विचार इरविन श्रोडिंगर द्वारा क्वांटम-यांत्रिकी के एक संपूर्ण सिद्धांत के रूप में विकसित किया गया, जिसे सामान्यतः तरंग-यांत्रिकी कहते हैं| इलेक्ट्रॉनों की तरंग प्रकृति की खोज के लिए इन्हें सन् 1929 में नोबेल पुरस्कार से सम्मानित किया गया|
समीकरण (11.12) इस संभावना की अनुमति देता है कि ∆x शून्य हो; परंतु तब ∆ p को अनंत होना चाहिए जिससे कि गुणनफल शून्य न हो| इसी प्रकार यदि ∆p शून्य होता है, तब ∆x अनंत होगा| सामान्यतया, दोनों ∆x तथा ∆p शून्य नहीं होते जिससे कि उनका गुणनफल ö कोटि का हो|
अब यदि एक इलेक्ट्रॉन निश्चित संवेग p ( अर्थात ∆p = 0) हो, तब दे ब्रॉग्ली संबंध के द्वारा, इसका तरंगदैर्घ्य (λ) निश्चित होगा| एक निश्चित (एकल) तरंगदैर्घ्य की तरंग का विस्तार संपूर्ण स्थान में होता है| बॉर्न की प्रायिकता व्याख्या से इसका अर्थ यह हुआ कि इलेक्ट्रॉन स्थान के किसी निश्चित क्षेत्र में स्थानीयित नहीं होगा| अर्थात्, इसकी स्थिति अनिश्चितता अनंत होगी (∆x → ∞) जो अनिश्चितता के सिद्धांत के साथ संगत है|
सामान्यतः इलेक्ट्रॉन के साथ जुड़ी पदार्थ-तरंग संपूर्ण आकाश में विस्तृत नहीं होती| यह एक तरंग-पैकेट के रूप में आकाश में एक निश्चित क्षेत्र में विस्तृत होता है| उस स्थिति में ∆x अनंत नहीं होता है बल्कि तरंग-पैकेट के विस्तार पर निर्भर इसका कोई परिमित मान होता है| आपको यह भी जानना चाहिए कि परिमित विस्तार की किसी तरंग-पैकेट का तरंगदैर्घ्य एकल नहीं होता| यह किसी केंद्रीय तरंगदैर्घ्य के आसपास विस्तृत तरंगदैर्घ्य से बनी होती है|
तब, दे ब्रॉग्ली के संबंध के द्वारा, इलेक्ट्रॉन के संवेग का भी एक विस्तार होगा – ∆p की अनिश्चितता| यह अनिश्चितता के संबंध से अपेक्षित है| गणितीय ढंग (उपपत्ति छोड़ दी गई है) से यह दर्शाया जा सकता है कि तरंग-पैकेट विवरण दे ब्रॉग्ली संबंध तथा बॉर्न-प्रायिकता व्याख्या के साथ हाइजेनबर्ग अनिश्चितता-संबंध का परिशुद्ध रूप में पुनरुत्पन्न करता है|
अध्याय 12 में, दे ब्रॉग्ली संबंध को किसी परमाणु में इलेक्ट्रॉन के कोणीय संवेग के क्वांटमीकरण पर बोर की परिकल्पना की समर्थता को दर्शाते हुए पाएँगे|
चित्र 11.6(a) में एक स्थानीयित तरंग-पैकेट तथा चित्र 11.6(b) में निश्चित तरंगदैर्घ्य के लिए विस्तृत तरंग का व्यवस्था-चित्र दर्शाया गया है|
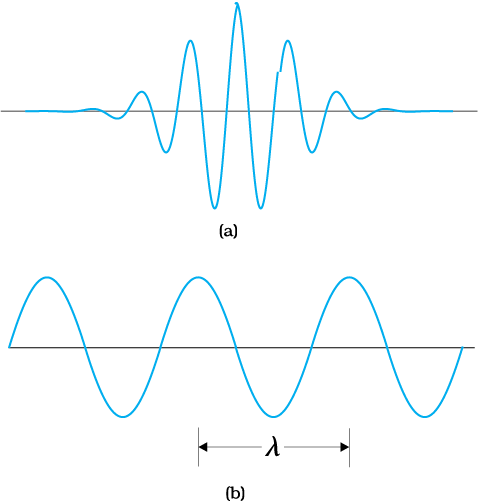
चित्र 11.6 (a) एक इलेक्ट्रॉन का तरंग-पैकेट विवरण| किसी बिंदु के आयाम के वर्ग को उस बिंदु पर इलेक्ट्रॉन की प्रायिकता घनत्व के साथ संबंधित किया गया है| तरंग-पैकेट किसी केंद्रीय तरंगदैर्घ्य के आसपास तरंगदैर्घ्य के विस्तार (और इस प्रकार दे ब्रॉग्ली संबंध के द्वारा, संवेग के विस्तार) के साथ मेल रखता है| परिणामतः, यह स्थिति में अनिश्चितता (∆x) और संवेग में अनिश्चितता (∆p) से जुड़ा है| (b) किसी इलेक्ट्रॉन के निश्चित संवेग से मेल खाती द्रव्य-तरंग संपूर्ण आकाश में विस्तृत होती है| इस उदाहरण में ∆p = 0 और ∆ x→ ∞|
उदाहरण 11.4 (a) एक इलेक्ट्रॉन जो 5.4×106 m/s की चाल से गति कर रहा है,
(b) 150 g द्रव्यमान की एक गेंद जो 30.0 m/s की चाल से गति कर रही है, से जुड़ी दे ब्रॉग्ली तरंगदैर्घ्य क्या होगी?
हल
(a) इलेक्ट्रॉन के लिए
द्रव्यमान m = 9.11 × 10–31 kg, वेग v = 5.4×106 m/s
तब संवेग p = m v = 9.11×10–31 (kg) × 5.4 × 106 (m/s)
p = 4.92 × 10–24 kg m/s
दे ब्रॉग्ली तरंगदैर्घ्य, λ = h/p
= 
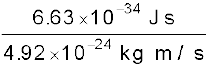
λ = 0.135 nm
(b) गेंद के लिए
द्रव्यमान m' = 0.150 kg, वेग v' = 30.0 m/s
तब संवेग
p' = m' v' = 0.150 (kg) × 30.0 (m/s)
p' = 4.50 kg m/s
दे ब्रॉग्ली तरंगदैर्घ्य λ' = h/p'
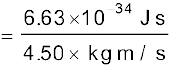
λ' = 1.47 ×10–34 m
इलेक्ट्रॉन के लिए दे ब्रॉग्ली तरंगदैर्घ्य X-किरण तरंगदैर्घ्य के समान है| परंतु गेंद के लिए यह प्रोटॉन के आकार के लगभग 10–19 गुना है जो प्रायोगिक मापन की सीमा के बिलकुल बाहर है|
उदाहरण 11.5 एक इलेक्ट्रॉन, एक α-कण तथा एक प्रोटॉन की गतिज ऊर्जा समान हैं| इनमें से किस कण की दे ब्रॉग्ली तरंगदैर्घ्य न्यूनतम होगी?
हल
किसी कण के लिए, दे ब्रॉग्ली तरंगदैर्घ्य λ = h/p है|
गतिज ऊर्जा K = p2/2m
अतः,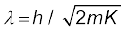 
समान गतिज ऊर्जा K के लिए किसी कण से संबद्ध दे ब्रॉग्ली तरंगदैर्घ्य उसके द्रव्यमान के वर्गमूल के व्युत्क्रमानुपाती है| प्रोटॉन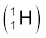 
इलेक्ट्रॉन से 1836 गुना भारी है तथा α-कण 
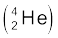प्रोटॉन से चार गुना भारी है|
अतः α – कण की दे ब्रॉग्ली तरंगदैर्घ्य न्यूनतम होगी|
द्रव्य तरंगों का प्रायिकता अर्थ
यहाँ इस बात पर विचार करना उचित होगा कि किसी कण (जैसे इलेक्ट्रॉन), से संबंधित द्रव्य-तरंग का क्या अर्थ है| वास्तव में, अभी तक द्रव्य तथा विकिरण के द्वैत प्रकृति की एक वस्तुतः संतोषजनक भौतिक समझ विकसित नहीं हो सकी है| क्वांटम-यांत्रिकी के महान संस्थापकों (नील्स बोहर, अल्बर्ट आइंस्टाइन और कई अन्य) ने इस तथा इससे संबंधित संकल्पनाओं के साथ बहुत समय तक संघर्ष किया| अब भी क्वांटम-यांत्रिकी की गहन भौतिक व्याख्या सक्रिय शोध का विषय बना हुआ है| इसके होते हुए भी, द्रव्य-तरंग की संकल्पना को बड़ी सफलता के साथ आधुनिक क्वांटम-यांत्रिकी में गणितीय तौर पर प्रविष्ट किया गया है| इस संबंध में एक महत्वपूर्ण उपलब्धि यह है कि जब मैक्स बॉर्न(1882-1970) ने द्रव्य-तरंग के आयाम की एक प्रायिकता-व्याख्या सुझाई| इसके अनुसार, किसी बिंदु पर द्रव्य-तरंग की तीव्रता (आयाम का वर्ग) उस बिंदु पर कण का प्रायिकता-घनत्व निर्धारित करता है| प्रायिकता घनत्व का अर्थ प्रायिकता प्रति इकाई आयतन है| इस प्रकार, यदि किसी बिंदु पर A तरंग का आयाम है तो |A|2 ∆V उस बिंदु के चारों ओर ∆V लघु आयतन में उस कण के पाए जाने की प्रायिकता है| अतः किसी विशिष्ट क्षेत्र में यदि द्रव्य-तरंग की तीव्रता अधिक है, तब उसकी तुलना में जहाँ तीव्रता कम है, कण के पाए जाने की प्रायिकता अधिक होगी|
उदाहरण 11.6 एक कण, इलेक्ट्रॉन की अपेक्षा तीन गुना अधिक चाल से गति कर रहा है| इस कण की दे ब्रॉग्ली तरंगदैर्घ्य का इलेक्ट्रॉन की दे ब्रॉग्ली तरंगदैर्घ्य से अनुपात 1.813 × 10–4 है| कण के द्रव्यमान का परिकलन कीजिए तथा कण को पहचानिए|
हल
गति करते हुए कण (द्रव्यमान m तथा वेग v) की दे ब्रॉग्ली तरंगदैर्घ्य
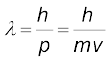
द्रव्यमान m = h/λv
इलेक्ट्रॉन का द्रव्यमान me = h/λe ve
हमें ज्ञात है कि v/ve = 3 तथा
λ/λe = 1.813 × 10–4
कण का द्रव्यमान, m = me 
m = (9.11×10–31 kg) × (1/3) × (1/1.813 × 10–4)
m = 1.675 × 10–27 kg
इस द्रव्यमान का कण प्रोटॉन या न्यूट्रॉन हो सकता है|
उदाहरण 11.7 100 V के विभवांतर द्वारा त्वरित किसी इलेक्ट्रॉन से संबंधित दे ब्रॉग्ली तरंगदैर्घ्य का परिकलन कीजिए|
हल त्वरक विभव V = 100 V
दे ब्रॉग्ली तरंगदैर्घ्य λ होगी
λ = h /p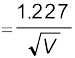 
nm
λ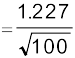 
nm = 0.123 nm
इलेक्ट्रॉन से संबंधित दे ब्रॉग्ली तरंगदैर्घ्य X-किरण तरंगदैर्घ्यों की कोटि की है|
11.9 डेविसन तथा जर्मर प्रयोग
इलेक्ट्रॉन की तरंग प्रकृति प्रायोगिक तौर पर सर्वप्रथम सी.जे. डेविसन तथा एल.एच. जर्मर के द्वारा 1927 में तथा स्वतंत्र रूप से जी.पी. टॉमसन के द्वारा 1928 में सत्यापित की गई थी| इन वैज्ञानिकों ने इलेक्ट्रॉनों के किरण-पुंज का क्रिस्टलों से प्रकीर्णन के द्वारा विवर्तन प्रभाव का प्रेक्षण किया था| सी.जे. डेविसन (1881-1958) और जी.पी. टॉमसन (1892-1975) ने क्रिस्टल के द्वारा इलेक्ट्रॉनों के विवर्तन की प्रायोगिक खोज के लिए 1937 में संयुक्त रूप से नोबेल पुरस्कार प्राप्त किया|
डेविसन तथा जर्मर की प्रायोगिक व्यवस्था चित्र 11.7 में दर्शायी गई है| इसमें एक ‘इलेक्ट्रॉन गन’ होती है जो एक टंगस्टन तंतु F की बनी होती है, जिस पर बेरियम अॉक्साइड का लेप होता है| इसे कम विभव (L.T. बैटरी) से गर्म किया जाता है| किसी उच्च वोल्टता ऊर्जा स्रोत (HT बैटरी) द्वारा उपयुक्त विभव/वोल्टता के अनुप्रयोग से तंतु द्वारा उत्सर्जित इलेक्ट्रॉनों को एेच्छिक वेग तक त्वरित किया जाता है| इन्हें एक बेलन जिसमें इसके अक्ष के समांतर पतले छिद्र होते हैं, से पारित करके एक पतले किरण-पुंज के रूप में समांतरित कर लिया जाता है| इस किरण-पुंज को एक निकिल क्रिस्टल के पृष्ठ पर डाला जाता है| क्रिस्टल के परमाणुओं के द्वारा इलेक्ट्रॉन सभी दिशाओं में प्रकीर्णित होते हैं| किसी दिशा में प्रकीर्णित इलेक्ट्रॉन किरण-पुंज की तीव्रता को इलेक्ट्रॉन संसूचक (संग्राहक) के द्वारा मापा जाता है| संसूचक को वृत्ताकार मापनी पर घुमाया जा सकता है और एक सुग्राही गैल्वेनोमीटर के साथ संयोजित कर दिया जाता है, जो धारा को अंकित करता है| गैल्वेनोमीटर में विक्षेप संग्राहक में प्रवेश करने वाले इलेक्ट्रॉन किरण-पुंज की तीव्रता के अनुक्रमानुपाती होता है| इस उपकरण को एक निर्वातित कोष्ठ में परिबद्ध कर देते हैं| संसूचक को वृत्ताकार मापनी पर विभिन्न स्थितियों में घुमाकर, प्रकीर्णित इलेक्ट्रॉन किरण-पुंज की तीव्रता को विभिन्न अक्षांश कोण के मान के लिए (अथवा प्रकीर्णन के कोण) θ को मापते हैं, जो कि आपतित और प्रकीर्णित इलेक्ट्रॉन किरण पुंजों के बीच का कोण होता है| प्रकीर्णित इलेक्ट्रॉनों की तीव्रता (I) में प्रकीर्णन कोण θ के साथ परिवर्तन को विभिन्न त्वरण विभवों के लिए प्राप्त किया जाता है|
त्वरक विभव के 44 V से 68 V के परास के लिए इस प्रयोग को संपन्न किया गया डेविसन-जर्मर प्रयोग के परिणामों को दर्शाया गया है| यह पाया गया कि एक तीक्ष्ण विवर्तन उच्चिष्ठ के संगत एक प्रबल शिखर, त्वरक विभव 54 V तथा प्रकीर्णन कोण θ = 50o पर इलेक्ट्रॉन वितरण में, प्रकट होती है| एक विशिष्ट दिशा में शिखर का यह प्रकटन क्रिस्टल के परमाणुओं के समान अंतराल की परतों से इलेक्ट्रॉनों के संपोषी व्यतिकरण के कारण होता है| इलेक्ट्रॅान विवर्तन मापन से द्रव्य-तरंग का तरंगदैर्घ्य 0.165 nm प्राप्त किया गया|
दे ब्रॉग्ली तरंगदैर्घ्य λ [समीकरण (11.11) के उपयोग से] V = 54 V के लिए इलेक्ट्रॉन का मान निम्न होगा ः
λ = h /p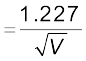 
nm
λ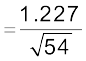 
nm = 0.167 nm
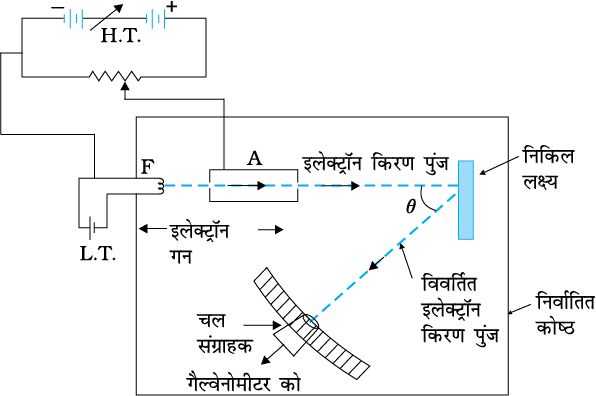
चित्र 11.7 डेविसन-जर्मर इलेक्ट्रॉन विवर्तन व्यवस्था|
दे ब्रॉग्ली की परिकल्पना आधुनिक क्वांटम यांत्रिकी के विकास में आधार रही है| इसने इलेक्ट्रॉन-प्रकाशिकी विषय को भी विकसित किया है| इलेक्ट्रॉन के तरंगीय गुणों का उपयोग इलेक्ट्रॉन-सूक्ष्मदर्शी के निर्माण में किया गया है, जो प्रकाश-सूक्ष्मदर्शी की तुलना में उच्चतर विभेदन के कारण एक बहुत बड़ा सुधार है|
सारांश
1. किसी इलेक्ट्रॉन को धातु से बाहर निकालने के लिए न्यूनतम ऊर्जा को धातु का कार्य-फलन कहते हैं| धातु-पृष्ठ से इलेक्ट्रॉन-उत्सर्जन के लिए आवश्यक ऊर्जा (कार्य-फलन φο से अधिक) को उपयुक्त तापन अथवा प्रबल विद्युत क्षेत्र अथवा उपयुक्त आवृत्ति के प्रकाश द्वारा विकिरित करने से दी जा सकती है|
2. प्रकाश-विद्युत प्रभाव धातुओं से उपयुक्त आवृत्ति के प्रकाश से प्रदीप्त करने पर इलेक्ट्रॉनों के उत्सर्जन की परिघटना है| कुछ धातु पराबैंगनी प्रकाश से प्रतिक्रिया करते हैं जबकि दूसरे दृश्य-प्रकाश के लिए भी सुग्राही हैं| प्रकाश-विद्युत प्रभाव में प्रकाश ऊर्जा का वैद्युत ऊर्जा में रूपांतरण होता है| यह ऊर्जा के संरक्षण के नियम का पालन करता है| प्रकाश-विद्युत उत्सर्जन एक तात्क्षणिक प्रक्रिया है और इसके कुछ विशिष्ट लक्षण होते हैं|
3. प्रकाश-विद्युत धारा (i) आपतित प्रकाश की तीव्रता, (ii) दो इलेक्ट्रोडों के बीच लगाया गया विभवांतर, और (iii) उत्सर्जक के पदार्थ की प्रकृति पर निर्भर करती है|
4. रोधक विभव (Vo) (i) आपतित प्रकाश की आवृत्ति और (ii) उत्सर्जक पदार्थ की प्रकृति पर निर्भर करता है| आपतित प्रकाश की किसी दी हुई आवृत्ति के लिए, यह इसकी तीव्रता पर निर्भर नहीं करता है| रोधक विभव का उत्सर्जित इलेक्ट्रॉनों की उच्चतम गतिज ऊर्जा से संबंधित हैः
e V0 = 
m v2उच्च = Kउच्च
5. एक निश्चित आवृत्ति (देहली आवृत्ति) ν0 के नीचे जो धातु का अभिलक्षण है, कोई प्रकाश-विद्युत उत्सर्जित नहीं होता चाहे आपतित प्रकाश की तीव्रता कितनी भी अधिक क्यों न हो|
6. क्लासिकी तरंग-सिद्धांत प्रकाश-विद्युत प्रभाव के मुख्य लक्षणों की व्याख्या नहीं कर सका| इसका विकिरण से ऊर्जा का संतत अवशोषण का चित्रण Kउच्चकी तीव्रता से स्वतंत्रता, νo के अस्तित्व और इस प्रक्रिया की तात्क्षणिक प्रकृति की व्याख्या नहीं कर सका| आइंस्टाइन ने इन लक्षणों की व्याख्या प्रकाश के फ़ोटॉन-चित्रण के आधार पर की| इसके अनुसार प्रकाश, ऊर्जा के विविक्त पैकेटों से बना है, जिन्हें क्वांटा अथवा फ़ोटॉन कहते हैं| प्रत्येक फोटॉन की ऊर्जा E (= h ν) और संवेग p (= h/λ) होता है, जो कि आपतित प्रकाश की आवृत्ति (ν ) पर निर्भर करते हैं परंतु इसकी तीव्रता पर निर्भर नहीं करते| धातु के पृष्ठ से प्रकाश-विद्युत उत्सर्जन एक इलेक्ट्रॉन के द्वारा फ़ोटॉन के अवशोषण से होता है|
7. आइंस्टाइन का प्रकाश-विद्युत समीकरण ऊर्जा संरक्षण नियम के संगत है जैसा कि धातु में एक इलेक्ट्रॉन के द्वारा फ़ोटॉन अवशोषण में लागू होता है| उच्चतम गतिज ऊर्जा (
m v2उच्च) फ़ोटॉन-ऊर्जा (hν) तथा लक्ष्य धातु कार्य-फलन φ0 (= hν0) के अंतर के बराबर होती है|
m v2उच्च = V0 e = hν – φ0 = h (ν – ν0)
इस प्रकाश-विद्युत समीकरण से प्रकाश-विद्युत प्रभाव के सभी लक्षणों की व्याख्या होती है| मिलिकन के प्रथम परिशुद्ध प्रकाश-विद्युत मापनों ने आइंस्टाइन के प्रकाश-विद्युत समीकरण को संपुष्ट किया और प्लैंक-स्थिरांक (h) के यथार्थ मान को प्राप्त किया| इससे आइंस्टाइन द्वारा प्रवर्तित वैद्युतचुंबकीय विकिरण का कण अथवा फ़ोटॉन वर्णन (प्रकृति) स्वीकृत हुआ|
8. विकिरण की द्वैत प्रकृति होती है : तरंग तथा कण| प्रयोग के स्वरूप पर यह निर्धारित होता है कि तरंग अथवा कण के रूप में वर्णन प्रयोग के परिणाम को समझने के लिए सर्वाधिक उपयुक्त है| इस तर्क के साथ कि विकिरण तथा पदार्थ प्रकृति में सममित हैं, लुइस दे ब्रॉग्ली के पदार्थ (पदार्थ कणों) को तरंग जैसा लक्षण प्रदान किया| गतिमान पदार्थ-कणों से जुड़ी तरंगों को पदार्थ तरंग अथवा दे ब्रॉग्ली तरंग कहते हैं|
9. गतिमान कण से संबंधित दे ब्रॉग्ली तरंगदैर्घ्य (λ) इसके संवेग p से इस प्रकार संबंधित है :
λ = h/p | पदार्थ का द्वैत दे ब्रॉग्ली संबंध, जिसमें तरंग संकल्पना (λ) और कण संकल्पना (p) सम्मिलित हैं, में अंतर्निष्ठ है| दे ब्रॉग्ली तरंगदैर्घ्य पदार्थ-कण के आवेश तथा इसकी प्रकृति से स्वतंत्र है| यह सार्थकताः केवल उप-परमाण्विक कणों, जैसे – इलेक्ट्रॉन, प्रोटॉन आदि (इनके द्रव्यमान अर्थात संवेग की लघुता के कारण) के लिए ही परिमेय (क्रिस्टलों में परमाण्वीय समतलों के बीच की दूरी की कोटि का) है| तथापि यह वास्तव में उन स्थूल वस्तुओं के लिए जो सामान्यतः प्रतिदिन जीवन में मिलती हैं और मापन की सीमा के बिलकुल बाहर है, बहुत छोटा है|
10. डेविसन-जर्मर के तथा जी. पी. टॉमसन के द्वारा इलेक्ट्रॉन विवर्तन प्रयोगों तथा बाद के कई प्रयोगों ने इलेक्ट्रॉन की तरंग-प्रकृति को सत्यापित तथा पुष्ट किया है| पदार्थ तरंग की दे ब्रॉग्ली परिकल्पना, बोहर की स्थायी कक्षा की संकल्पना का समर्थन करती है|
विचारणीय विषय
1. किसी धातु में मुक्त इलेक्ट्रॉन इस अर्थ में मुक्त हैं कि वे धातु के भीतर एक स्थिर विभव के अंतर्गत गतिमान होते हैं (यह केवल एक सन्निकटन है)| वे धातु के बाहर निकलने के लिए मुक्त नहीं होते हैं| उन्हें धातु से बाहर जाने के लिए अतिरिक्त ऊर्जा की आवश्यकता होती है|
2. किसी धातु में सभी मुक्त इलेक्ट्रॉनों की ऊर्जा समान नहीं होती| किसी गैस जार में अणुओं के जैसे, एक दिए गए ताप पर इलेक्ट्रॉनों का एक निश्चित ऊर्जा वितरण होता है| यह वितरण उस सामान्य मैक्सवेल वितरण से भिन्न होता है जिसे आप गैसों के गतिज सिद्धांत के अध्ययन में पढ़ चुके हैं| इसके विषय में आप बाद के पाठ्यक्रमों में जानेंगे, परंतु भिन्नता का संबंध इस तथ्य से है कि इलेक्ट्रॉन पॉली के अपवर्जन के सिद्धांत का अनुसरण करते हैं|
3. किसी धातु में मुक्त इलेक्ट्रॉनों के ऊर्जा वितरण के कारण, धातु से बाहर आने के लिए इलेक्ट्रॉन के द्वारा अपेक्षित ऊर्जा भिन्न इलेक्ट्रॉनों के लिए भिन्न होती है| उच्चतर ऊर्जा वाले इलेक्ट्रॉनों की धातु से बाहर आने के लिए कम ऊर्जा वाले इलेक्ट्रॉनों की तुलना में कम अतिरिक्त ऊर्जा की आवश्यकता होती है| कार्य-फलन धातु से बाहर निकलने के लिए किसी इलेक्ट्रॉन के द्वारा अपेक्षित न्यूनतम ऊर्जा है|
4. प्रकाश-विद्युत प्रभाव से संबंधित प्रयोगों मे केवल यही अंतर्निहित है कि द्रव्य के साथ प्रकाश की अन्योन्य क्रिया में ऊर्जा का अवशोषण hν की विविक्त इकाइयों में होता है| यह बिलकुल ही एेसा कहने के समान नहीं है कि प्रकाश एेसे कणों से बना है जिनमें प्रत्येक की ऊर्जा hν है|
5. निरोधी विभव पर प्रेक्षण (इसकी तीव्रता पर अनिर्भरता और आवृत्ति पर निर्भरता) प्रकाश-विद्युत प्रभाव के तरंग-चित्रण और फ़ोटॉन-चित्रण के बीच निर्णायक विभेदकारक है|
6. सूत्र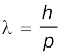 
के द्वारा दिया गया पदार्थ-तरंग का तरंगदैर्घ्य का भौतिकीय महत्त्व है, इसके कला-वेग vp का कोई भौतिकीय महत्त्व नहीं होता है| तथापि, पदार्थ-तरंग का समूह-वेग भौतिकतया अर्थपूर्ण है और कण के वेग के बराबर होता है|
अभ्यास
11.1 30 kV इलेक्ट्रॉनों के द्वारा उत्पन्न X-किरणों की (a) उच्चतम आवृत्ति तथा (b) निम्नतम तरंगदैर्घ्य प्राप्त कीजिए|
11.2 सीज़ियम धातु का कार्य-फलन 2.14 eV है| जब 6 ×1014Hz आवृत्ति का प्रकाश धातु-पृष्ठ पर आपतित होता है, इलेक्ट्रॉनों का प्रकाशिक उत्सर्जन होता है|
(a) उत्सर्जित इलेक्ट्रॉनों की उच्चतम गतिज ऊर्जा,
(b) निरोधी विभव, और
(c) उत्सर्जित प्रकाशिक इलेक्ट्रॉनों की उच्चतम चाल कितनी है?
11.3 एक विशिष्ट प्रयोग में प्रकाश-विद्युत प्रभाव की अंतक वोल्टता 1.5 V है| उत्सर्जित प्रकाशिक इलेक्ट्रॉनों की उच्चतम गतिज ऊर्जा कितनी है?
11.4 632.8 nm तरंगदैर्घ्य का एकवर्णी प्रकाश एक हीलियम-नियॉन लेसर के द्वारा उत्पन्न किया जाता है| उत्सर्जित शक्ति 9.42 mW है|
(a) प्रकाश के किरण-पुंज में प्रत्येक फ़ोटॉन की ऊर्जा तथा संवेग प्राप्त कीजिए,
(b) इस किरण-पुंज के द्वारा विकिरित किसी लक्ष्य पर औसतन कितने फ़ोटॉन प्रति सेकंड पहुँचेंगे? (यह मान लीजिए कि किरण-पुंज की अनुप्रस्थ काट एकसमान है जो लक्ष्य के क्षेत्रफल से कम है), तथा
(c) एक हाइड्रोजन परमाणु को फ़ोटॉन के बराबर संवेग प्राप्त करने के लिए कितनी तेज़ चाल से चलना होगा?
11.5 पृथ्वी के पृष्ठ पर पहुँचने वाला सूर्य-प्रकाश का ऊर्जा-अभिवाह (फ्लक्स) 1.388 × 103 W/m2 है| लगभग कितने फ़ोटॉन प्रति वर्ग मीटर प्रति सेकंड पृथ्वी पर आपतित होते हैं? यह मान लें कि सूर्य-प्रकाश में फ़ोटॉन का औसत तरंगदैर्घ्य 550 nm है|
11.6 प्रकाश-विद्युत प्रभाव के एक प्रयोग में, प्रकाश आवृत्ति के विरुद्ध अंतक वोल्टता की ढलान 4.12 × 10–15 V s प्राप्त होती है| प्लांक स्थिरांक का मान परिकलित कीजिए|
11.7 एक 100 W सोडियम बल्ब (लैंप) सभी दिशाओं में एकसमान ऊर्जा विकिरित करता है| लैंप को एक एेसे बड़े गोले के केंद्र पर रखा गया है जो इस पर आपतित सोडियम के संपूर्ण प्रकाश को अवशोषित करता है| सोडियम प्रकाश का तरंगदैर्घ्य 589 nm है| (a) सोडियम प्रकाश से जुड़े प्रति फ़ोटॉन की ऊर्जा कितनी है? (b) गोले को किस दर से फ़ोटॉन प्रदान किए जा रहे हैं?
11.8 किसी धातु की देहली आवृत्ति 3.3 × 1014 Hz है| यदि 8.2 × 1014 Hz आवृत्ति का प्रकाश धातु पर आपतित हो, तो प्रकाश-विद्युत उत्सर्जन के लिए अंतक वोल्टता ज्ञात कीजिए|
11.9 किसी धातु के लिए कार्य-फलन 4.2 eV है| क्या यह धातु 330 nm तरंगदैर्घ्य के आपतित विकिरण के लिए प्रकाश-विद्युत उत्सर्जन देगा?
11.10 7.21 × 1014 Hz आवृत्ति का प्रकाश एक धातु-पृष्ठ पर आपतित है| इस पृष्ठ से
6.0 × 105 m/s की उच्चतम गति से इलेक्ट्रॉन उत्सर्जित हो रहे हैं| इलेक्ट्रॉनों के प्रकाश उत्सर्जन के लिए देहली आवृत्ति क्या है?
11.11 488 nm तरंगदैर्घ्य का प्रकाश एक अॉर्गन लेसर से उत्पन्न किया जाता है, जिसे प्रकाश-विद्युत प्रभाव के उपयोग में लाया जाता है| जब इस स्पेक्ट्रमी-रेखा के प्रकाश को उत्सर्जक पर आपतित किया जाता है तब प्रकाशिक इलेक्ट्रॉनों का निरोधी (अंतक) विभव 0.38 V है| उत्सर्जक के पदार्थ का कार्य-फलन ज्ञात करें|
11.12 56 V विभवांतर के द्वारा त्वरित इलेक्ट्रॉनों का
(a) संवेग, और
(b) दे ब्रॉग्ली तरंगदैर्घ्य परिकलित कीजिए|
11.13 एक इलेक्ट्रॉन जिसकी गतिज ऊर्जा 120 eV है, उसका
(a) संवेग, (b) चाल और (c) दे ब्रॉग्ली तरंगदैर्घ्य क्या है?
11.14 सोडियम के स्पेक्ट्रमी उत्सर्जन रेखा के प्रकाश का तरंगदैर्घ्य 589 nm है| वह गतिज ऊर्जा ज्ञात कीजिए जिस पर
(a) एक इलेक्ट्रॉन, और (b) एक न्यूट्रॉन का दे ब्रॉग्ली तरंगदैर्घ्य समान होगा|
11.15 (a) एक 0.040 kg द्रव्यमान का बुलेट जो 1.0 km/s की चाल से चल रहा है, (b) एक 0.060 kg द्रव्यमान की गेंद जो 1.0 km/s की चाल से चल रही है, और (c) एक धूल-कण जिसका द्रव्यमान 1.0 × 10–9 kg और जो 2.2 m/s की चाल से अनुगमित हो रहा है, का दे ब्रॉग्ली तरंगदैर्घ्य कितना होगा?
11.16 एक इलेक्ट्रॉन और एक फ़ोटॉन प्रत्येक का तरंगदैर्घ्य 1.00 nm है|
(a) इनका संवेग,
(b) फोटॉन की ऊर्जा, और
(c) इलेक्ट्रॉन की गतिज ऊर्जा ज्ञात कीजिए|
11.17 (a) न्यूट्रॉन की किस गतिज ऊर्जा के लिए दे ब्रॉग्ली तरंगदैर्घ्य 1.40 × 10–10 m होगा?
(b) एक न्यूट्रॉन, जो पदार्थ के साथ तापीय साम्य में है और जिसकी 300 K पर औसत गतिज ऊर्जा 
k T है, का भी दे ब्रॉग्ली तरंगदैर्घ्य ज्ञात कीजिए|
11.18 यह दर्शाइए कि वैद्युतचुंबकीय विकिरण का तरंगदैर्घ्य इसके क्वांटम (फ़ोटॉन) के तरंगदैर्घ्य के बराबर है|
11.19 वायु में 300 K ताप पर एक नाइट्रोजन अणु का दे ब्रॉग्ली तरंगदैर्घ्य कितना होगा? यह मानें कि अणु इस ताप पर अणुओं के चाल वर्ग माध्य से गतिमान है| (नाइट्रोजन का परमाणु द्रव्यमान = 14.0076 u)
अतिरिक्त अभ्यास
11.20 (a) एक निर्वात नली के तापित कैथोड से उत्सर्जित इलेक्ट्रॉनों की उस चाल का आकलन कीजिए जिससे वे उत्सर्जक की तुलना में 500 V के विभवांतर पर रखे गए एनोड से टकराते हैं| इलेक्ट्रॉनों के लघु प्रारंभिक चालों की उपेक्षा कर दें| इलेक्ट्रॉन का आपेक्षिक आवेश अर्थात e/m 1.76 × 1011 C kg–1 है|
(b) संग्राहक विभव 10 MV के लिए इलेक्ट्रॉन की चाल ज्ञात करने के लिए उसी सूत्र का प्रयोग करें, जो (a) में काम में लाया गया है| क्या आप इस सूत्र को गलत पाते हैं? इस सूत्र को किस प्रकार सुधारा जा सकता है?
11.21 (a) एक समोर्जी इलेक्ट्रॉन किरण-पुंज जिसमें इलेक्ट्रॉन की चाल 5.20 × 106 m s–1 है, पर एक चुंबकीय क्षेत्र 1.30 × 10–4 T किरण-पुंज की चाल के लंबवत लगाया जाता है| किरण-पुंज द्वारा आरेखित वृत्त की त्रिज्या कितनी होगी, यदि इलेक्ट्रॉन के e/m का मान 1.76 × 1011 C kg–1 है|
(b) क्या जिस सूत्र को (a) में उपयोग में लाया गया है वह यहाँ भी एक 20 MeV इलेक्ट्रॉन किरण-पुंज की त्रिज्या परिकलित करने के लिए युक्तिपरक है? यदि नहीं तो किस प्रकार इसमें संशोधन किया जा सकता है?
[नोट : अभ्यास 11.20 (b) तथा 11.21 (b) आपको आपेक्षिकीय यांत्रिकी तक ले जाते हैं जो इस पुस्तक के विषय के बाहर है| यहाँ पर इन्हें इस बिंदु पर बल देने के लिए सम्मिलित किया गया है कि जिन सूत्रों को आप (a) में उपयोग में लाते हैं वे बहुत उच्च चालों अथवा ऊर्जाओं पर युक्तिपरक नहीें होते| यह जानने के लिए कि ‘बहुत उच्च चाल अथवा ऊर्जा’ का क्या अर्थ है? अंत में दिए गए उत्तरों को देखें]
11.22 एक इलेक्ट्रॉन गन जिसका संग्राहक 100 V विभव पर है, एक कम दाब (∼10–2 mm Hg) पर हाइड्रोजन से भरे गोलाकार बल्ब में इलेक्ट्रॉन छोड़ती है| एक चुंबकीय क्षेत्र जिसका मान 2.83 × 10–4 T है, इलेक्ट्रॉन के मार्ग को 12.0 cm त्रिज्या के वृत्तीय कक्षा में वक्रित कर देता है| (इस मार्ग को देखा जा सकता है क्योंकि मार्ग में गैस आयन किरण-पुंज को इलेक्ट्रॉनों को आकर्षित करके और इलेक्ट्रॉन प्रग्रहण के द्वारा प्रकाश उत्सर्जन करके फ़ोकस करते हैं; इस विधि को ‘परिष्कृत किरण-पुंज नली’ विधि कहते हैं|) आँकड़ों से e/m का मान निर्धारित कीजिए|
11.23 (a) एक X-किरण नली विकिरण का एक संतत स्पेक्ट्रम जिसका लघु तरंगदैर्घ्य सिरा 0.45 Å पर है, उत्पन्न करता है| विकिरण में किसी फ़ोटॉन की उच्चतम ऊर्जा कितनी है?
(b) अपने (a) के उत्तर से अनुमान लगाइए कि किस कोटि की त्वरक वोल्टता (इलेक्ट्रॉन के लिए) की इस नली में आवश्यकता है?
11.24 एक त्वरित्र (accelerator) प्रयोग में पाज़िट्रॉनों (e+) के साथ इलेक्ट्रॉनों के उच्च-ऊर्जा संघट्टन पर, एक विशिष्ट घटना की व्याख्या कुल ऊर्जा 10.2 BeV के इलेक्ट्रॉन-पाज़िट्रॉन युग्म के बराबर ऊर्जा की दो γ-किरणों में विलोपन के रूप में की जाती है| प्रत्येक γ-किरण से संबंधित तरंगदैर्घ्यों के मान क्या होंगे? (1BeV = 109 eV)
11.25 आगे आने वाली दो संख्याओं का आकलन रोचक हो सकता है| पहली संख्या यह बताएगी कि रेडियो अभियांत्रिक फ़ोटॉन की अधिक चिंता क्यों नहीं करते| दूसरी संख्या आपको यह बताएगी कि हमारे नेत्र ‘फ़ोटॉनों की गिनती’ क्यों नहीं कर सकते, भले ही प्रकाश साफ़-साफ़ संसूचन योग्य हो|
(a) एक मध्य तरंग (medium wave) 10 kW सामर्थ्य के प्रेषी, जो 500 m तरंगदैर्घ्य की रेडियो तरंग उत्सर्जित करता है, के द्वारा प्रति सेकंड उत्सर्जित फ़ोटॉनों की संख्या|
(b) निम्नतम तीव्रता का श्वेत प्रकाश जिसे हम देख सकते हैं (∼10–10 W m–2) के संगत फोटॉनों की संख्या जो प्रति सेकंड हमारे नेत्रों की पुतली में प्रवेश करती है| पुतली का क्षेत्रफल लगभग 0.4 cm2 और श्वेत प्रकाश की औसत आवृत्ति को लगभग 6 × 1014 Hz मानिए|
11.26 एक 100 W पारद (Mercury) स्रोत से उत्पन्न 2271 Å तरंगदैर्घ्य का पराबैंगनी प्रकाश एक मालिब्डेनम धातु से निर्मित प्रकाश सेल को विकिरित करता है| यदि निरोधी विभव
–1.3 V हो, तो धातु के कार्य-फलन का आकलन कीजिए| एक He-Ne लेसर द्वारा उत्पन्न 6328 Å के उच्च तीव्रता (∼105 W m–2) के लाल प्रकाश के साथ प्रकाश सेल किस प्रकार अनुक्रिया करेगा?
11.27 एक नियॉन लैंप से उत्पन्न 640.2 nm (1nm = 10–9 m) तरंगदैर्घ्य का एकवर्णी विकिरण टंगस्टन पर सीज़ियम से निर्मित प्रकाश-संवेदी पदार्थ को विकिरित करता है| निरोधी वोल्टता 0.54 V मापी जाती है| स्रोत को एक लौह-स्रोत से बदल दिया जाता है| इसकी 427.2 nm वर्ण-रेखा उसी प्रकाश सेल को विकिरित करती है| नयी निरोधी वोल्टता ज्ञात कीजिए|
11.28 एक पारद लैंप, प्रकाश-विद्युत उत्सर्जन की आवृत्ति निर्भरता के अध्ययन के लिए एक सुविधाजनक स्रोत है, क्योंकि यह दृश्य-स्पेक्ट्रम के पराबैंगनी (UV) से लाल छोर तक कई वर्ण-रेखाएँ उत्सर्जित करता है| रूबीडियम प्रकाश सेल के हमारे प्रयोग में, पारद (Mercury) स्रोत की निम्न वर्ण-रेखाओं का प्रयोग किया गया ः
λ1 = 3650 Å, λ2= 4047 Å, λ3= 4358 Å, λ4= 5461 Å, λ5= 6907 Å,
निरोधी वोल्टताएँ, क्रमशः निम्न मापी गईं :
V01 = 1.28 V, V02 = 0.95 V, V03 = 0.74 V, V04 = 0.16 V, V05 = 0 V
(a) प्लैंक स्थिरांक h का मान ज्ञात कीजिए|
(b) धातु के लिए देहली आवृत्ति तथा कार्य-फलन का आकलन कीजिए|
[नोट : उपर्युक्त आँकड़ों से h का मान ज्ञात करने के लिए आपको e = 1.6 × 10–19 C की आवश्यकता होगी| इस प्रकार के प्रयोग Na, Li, K आदि के लिए मिलिकन ने किए थे| मिलिकन ने अपने तेल-बूँद प्रयोग से प्राप्त e के मान का उपयोग कर आइंस्टाइन के प्रकाश- विद्युत समीकरण को सत्यापित किया तथा इन्हीं प्रेक्षणों से h के मान के लिए पृथक् अनुमान लगाया|]
11.29 निम्न धातुओं के कार्य-फलन निम्न प्रकार दिए गए हैं :
Na: 2.75 eV; K: 2.30 eV; Mo: 4.17 eV; Ni: 5.15 eV | इनमें धातुओं में से कौन प्रकाश सेल से 1 m दूर रखे गए He-Cd लेसर से उत्पन्न 3300 Å तरंगदैर्घ्य के विकिरण के लिए प्रकाश-विद्युत उत्सर्जन नहीं देगा? लेसर को सेल के निकट 50 cm दूरी पर रखने पर क्या होगा?
11.30 10–5 Wm–2 तीव्रता का प्रकाश एक सोडियम प्रकाश सेल के 2 cm2 क्षेत्रफल के पृष्ठ पर पड़ता है| यह मान लें कि ऊपर की सोडियम की पाँच परतें आपतित ऊर्जा को अवशोषित करती हैं, तो विकिरण के तरंग-चित्रण में प्रकाश-विद्युत उत्सर्जन के लिए आवश्यक समय का आकलन कीजिए| धातु के लिए कार्य-फलन लगभग 2 eV दिया गया है| आपके उत्तर का क्या निहितार्थ है|
11.31 X-किरणों के प्रयोग अथवा उपयुक्त वोल्टता से त्वरित इलेक्ट्रानों से क्रिस्टल-विवर्तन प्रयोग किए जा सकते हैं| कौन-सी जाँच अधिक ऊर्जा संबद्ध है? (परिमाणिक तुलना के लिए, जाँच के लिए तरंगदैर्घ्य को 1 Å लीजिए, जो कि जालक (लेटिस) में अंतर-परमाणु अंतरण की कोटि का है) (me=9.11 × 10–31 kg)|
11.32 (a) एक न्यूट्रॉन, जिसकी गतिज ऊर्जा 150 eV है, का दे ब्रॉग्ली तरंगदैर्घ्य प्राप्त कीजिए| जैसा कि आपने अभ्यास 11.31 में देखा है, इतनी ऊर्जा का इलेक्ट्रॉन किरण-पुंज क्रिस्टल विवर्तन प्रयोग के लिए उपयुक्त है| क्या समान ऊर्जा का एक न्यूट्रॉन किरण-पुंज इस प्रयोग के लिए समान रूप में उपयुक्त होगा? स्पष्ट कीजिए| (mn = 1.675 × 10–27 kg)
(b) कमरे के सामान्य ताप (27 °C) पर ऊष्मीय न्यूट्रॉन से जुड़े दे ब्रॉग्ली तरंगदैर्घ्य ज्ञात कीजिए| इस प्रकार स्पष्ट कीजिए कि क्यों एक तीव्रगामी न्यूट्रॉन को न्यूट्रॉन-विवर्तन प्रयोग में उपयोग में लाने से पहले वातावरण के साथ तापीकृत किया जाता है|
11.33 एक इलेक्ट्रॉन सूक्ष्मदर्शी में 50 kV वोल्टता के द्वारा त्वरित इलेक्ट्रॉनों का उपयोग किया जाता है| इन इलेक्ट्रॉनों से जुड़े दे ब्रॉग्ली तरंगदैर्घ्य ज्ञात कीजिए| यदि अन्य बातों (जैसे कि संख्यात्मक द्वारक, आदि) को लगभग समान लिया जाए, इलेक्ट्रॉन सूक्ष्मदर्शी की विभेदन क्षमता की तुलना पीले प्रकाश का प्रयोग करने वाले प्रकाश सूक्ष्मदर्शी से किस प्रकार होती है?
11.34 किसी जाँच की तरंगदैर्घ्य उसके द्वारा कुछ विस्तार में जाँच की जा सकने वाली संरचना के आकार की लगभग आमाप है| प्रोटॉनों तथा न्यूट्रॉनों की क्वार्क (quark) संरचना 10–15 m या इससे भी कम लंबाई के लघु पैमाने की है| इस संरचना को सर्वप्रथम 1970 दशक के प्रारंभ में, एक रेखीय त्वरित्र (Linear accelerator) से उत्पन्न उच्च ऊर्जा इलेक्ट्रॉनों के किरण-पुंजों के उपयोग द्वारा, स्टैनफ़ोर्ड, संयुक्त राज्य अमेरिका में जाँचा गया था| इन इलेक्ट्रॉन किरण-पुंजों की ऊर्जा की कोटि का अनुमान लगाइए| (इलेक्ट्रॉन की विराम द्रव्यमान ऊर्जा 0.511 MeV है|)
11.35 कमरे के ताप (27 °C) और 1 atm दाब पर He परमाणु से जुड़े प्रारूपी दे ब्रॉग्ली तरंगदैर्घ्य ज्ञात कीजिए और इन परिस्थितियों में इसकी तुलना दो परमाणुओं के बीच औसत दूरी से कीजिए|
11.36 किसी धातु में (27 °C) पर एक इलेक्ट्रॉन का प्रारूपी दे ब्रॉग्ली तरंगदैर्घ्य परिकलित कीजिए और इसकी तुलना धातु में दो इलेक्ट्रॉनों के बीच औसत पृथक्य से कीजिए जो लगभग 2 × 10–10 m दिया गया है|
[नोट ः अभ्यास 11.35 और 11.36 प्रदर्शित करते हैं कि जहाँ सामान्य परिस्थितियों में गैसीय अणुओं से जुड़े तरंग पैकेट अ-अतिव्यापी हैं; किसी धातु में इलेक्ट्रॉन तरंग पैकेट प्रबल रूप से एक-दूसरे से अतिव्यापी हैं| यह सुझाता है कि जहाँ किसी सामान्य गैस में अणुओं की अलग पहचान हो सकती है, किसी धातु में इलेक्ट्रॉन की एक-दूसरे से अलग पहचान नहीं हो सकती| इस अप्रभेद्यता के कई मूल निहितार्थताएँ हैं जिन्हें आप भौतिकी के अधिक उच्च पाठ्यक्रमों में जानेंगे|]
11.37 निम्न प्रश्नों के उत्तर दीजिए :
(a) एेसा विचार किया गया है कि प्रोटॉन और न्यूट्रॉन के भीतर क्वार्क पर आंशिक आवेश होते हैं [(+2/3)e ; (–1/3)e]| यह मिलिकन तेल-बूँद प्रयोग में क्यों नहीं प्रकट होते?
(b) e/m संयोग की क्या विशिष्टता है? हम e तथा m के विषय में अलग-अलग विचार क्यों नहीं करते?
(c) गैसें सामान्य दाब पर कुचालक होती हैं परंतु बहुत कम दाब पर चालन प्रारंभ कर देती हैं| क्यों?
(d) प्रत्येक धातु का एक निश्चित कार्य-फलन होता है| यदि आपतित विकिरण एकवर्णी हो तो सभी प्रकाशिक इलेक्ट्रॉन समान ऊर्जा के साथ बाहर क्यों नहीं आते हैं? प्रकाशिक इलेक्ट्रॉनों का एक ऊर्जा वितरण क्यों होता है?
(e) एक इलेक्ट्रॉन की ऊर्जा तथा इसका संवेग इससे जुड़े पदार्थ-तरंग की आवृत्ति तथा इसके तरंगदैर्घ्य के साथ निम्न प्रकार संबंधित होते हैं ः
E = hν, p = 
परंतु λ का मान जहाँ भौतिक महत्त्व का है, ν के मान (और इसलिए कला चाल ν λ
का मान) का कोई भौतिक महत्त्व नहीं है| क्यों?
परिशिष्ट