Table of Contents

अध्याय 13
नाभिक
13.1 भूमिका
पिछले अध्याय में हमने पढ़ा है कि प्रत्येक परमाणु का धनावेश घनीभूत होकर इसके केंद्र में संकेंद्रित हो जाता है और परमाणु का नाभिक बनाता है| नाभिक का कुल साइज़ परमाणु के साइज़ की तुलना में काफ़ी कम होता है| α-कणों के प्रकीर्णन संबंधी प्रयोगों ने यह प्रदर्शित किया है कि नाभिक की त्रिज्या, परमाणु की त्रिज्या की तुलना में 104 गुने से भी कम होनी चाहिए| इसका अर्थ है कि नाभिक का आयतन परमाणु के आयतन के 10–12 गुने के लगभग है| दूसरे शब्दों में कहें तो परमाणु में अधिकांशतः रिक्त स्थान ही है| यदि हम परमाणु का साइज़ बढ़ाकर कक्षा के कमरे के बराबर कर दें तो नाभिक इसमें एक पिन के शीर्ष के साइज़ का दिखाई देगा| तथापि, परमाणु का लगभग संपूर्ण द्रव्यमान (99.9% से अधिक) नाभिक में ही समाहित होता है|
परमाणु की संरचना के समरूप क्या नाभिक की भी कोई संरचना है? यदि एेसा है तो इसके अवयव क्या-क्या हैं? वे परस्पर किस प्रकार जुड़े हैं? इस अध्याय में हम इस प्रकार के प्रश्नोें के उत्तर खोजने का प्रयास करेंगे| हम नाभिकों के विशिष्ट गुणों, जैसे–उनके साइज़, द्रव्यमान तथा स्थायित्व की चर्चा के साथ इनसे संबद्ध रेडियोएेक्टिवता, विखंडन एवं संलयन जैसी नाभिकीय परिघटनाओं की भी विवेचन करेंगे|
13.2 परमाणु द्रव्यमान एवं नाभिक की संरचना
परमाणु का द्रव्यमान किलोग्राम की तुलना में बहुत कम होता है| उदाहरण के लिए, कार्बन के परमाणु 12C का द्रव्यमान 1.992647 × 10–26 kg है| इतनी छोटी राशियों को मापने के लिए किलोग्राम बहुत सुविधाजनक मात्रक नहीं है| अतः परमाणु द्रव्यमानों को व्यक्त करने के लिए द्रव्यमान का एक अन्य मात्रक प्रस्तुत किया गया| इस मात्रक को परमाणु द्रव्यमान मात्रक (u) कहते हैं| इसको 12C परमाणु के द्रव्यमान के बारहवें 1/12th भाग से व्यक्त करते हैं|
अतः इस परिभाषा के अनुसार
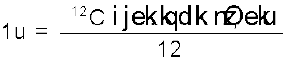
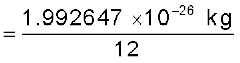
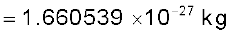 (13.1)
(13.1)
परमाणु द्रव्यमान मात्रक (u) में व्यक्त करने पर विभिन्न तत्वों के परमाणु द्रव्यमान, हाइड्रोजन परमाणु के द्रव्यमान के पूर्ण गुणज के निकट पाए जाते हैं| परंतु इस नियम के अनेक प्रभावशाली अपवाद भी हैं| उदाहरण के लिए, क्लोरीन का परमाणु द्रव्यमान 35.46 u है|
परमाणु द्रव्यमानों का यथार्थ मापन, द्रव्यमान वर्णक्रममापी (स्पेक्ट्रोमीटर) द्वारा किया जाता है| परमाणु द्रव्यमानों के मापन से पता चलता है कि एक ही तत्व के विभिन्न प्रकार के एेसे परमाणुओं का अस्तित्व है जिनके रासायनिक गुण तो समान होते हैं पर इनके द्रव्यमानों में अंतर होता है| एक ही तत्व की एेसी परमाणु प्रजातियाँ जिनके द्रव्यमानों में अंतर होता है, समस्थानिक कहलाती हैं (यूनानी शब्द आइसोटॉप का अर्थ हिंदी में समस्थानिक है, यह नाम इन्हें इसलिए दिया गया है क्योंकि तत्वों की आवर्त सारणी में ये सभी एक ही स्थान पर पाए जाते हैं)| शोध से पता चला कि प्रत्येक तत्व व्यावहारिक रूप से कई समस्थानिकों का मिश्रण है| विभिन्न समस्थानिकों की सापेक्ष बहुलता तत्व बदलने के साथ बदलती है|
उदाहरण के लिए, क्लोरीन के दो समस्थानिक हैं जिनके द्रव्यमान क्रमशः 34.98 u एवं 36.98 u हैं, जो कि हाइड्रोजन परमाणु द्रव्यमान के पूर्ण गुणज के सन्निकट हैं| इन समस्थानिकों की सापेक्ष बहुलता क्रमशः 75.4 एवं 24.6% है| इस प्रकार, प्राकृतिक क्लोरीन परमाणु का द्रव्यमान इन समस्थानिकों का भारित-औसत है| अतः, प्राकृतिक क्लोरीन परमाणु का द्रव्यमान,
= 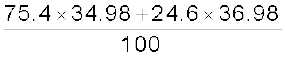
= 35.47 u
वही मान है जो क्लोरीन का परमाणु द्रव्यमान है|
यहाँ तक कि सबसे हलके तत्व हाइड्रोजन के भी तीन समस्थानिक हैं जिनके द्रव्यमान 1.0078 u, 2.0141 u एवं 3.0160 u हैं| सबसे हलके हाइड्रोजन परमाणु जिसकी सापेक्ष बहुलता 99.985 % है, का नाभिक, प्रोटॉन कहलाता है| एक प्रोटॉन का द्रव्यमान है,
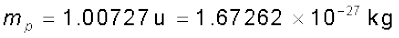 (13.2)
(13.2)
यह हाइड्रोजन परमाणु के द्रव्यमान 1.00783 u में से, इसमें विद्यमान एक इलेक्ट्रॉन के द्रव्यमान me = 0.00055 u को घटाने से प्राप्त द्रव्यमान के बराबर है| हाइड्रोजन के दूसरे दो समस्थानिक ड्यूटीरियम एवं ट्राइटियम कहलाते हैं| ट्राइटियम नाभिक अस्थायी होने के कारण प्रकृति में नहीं पाए जाते और कृत्रिम विधियों द्वारा प्रयोगशालाओं में निर्मित किए जाते हैं|
नाभिक में धन आवेश प्रोटॉनों का ही होता है| प्रोटॉन पर एकांक मूल आवेश होता है और यह स्थायी कण है| पहले यह विचार था कि नाभिक में इलेक्ट्रॉन होते हैं पर क्वांटम सिद्धांत पर आधारित तर्कों के कारण इस मान्यता को नकार दिया गया| किसी परमाणु के सभी इलेक्ट्रॉन उसके नाभिक के बाहर होते हैं| हम जानते हैं कि किसी परमाणु के नाभिक के बाहर इन इलेक्ट्रॉनों की संख्या उसके परमाणु क्रमांक Z, के बराबर होती है| अतः परमाणु में इलेक्ट्रॉनों का कुल आवेश (–Ze) उसके नाभिक के कुल आवेश (+Ze) के बराबर होता है, क्योंकि परमाणु विद्युतीय रूप से उदासीन होता है| इसलिए किसी परमाणु के नाभिक में प्रोटॉनोें की संख्या, तथ्यतः इसका परमाणु क्रमांक, Z होती है|
न्यूट्रॉन की खोज
क्योंकि ड्यूटीरियम एवं ट्राइटियम हाइड्रोजन के ही समस्थानिक हैं, इनमें से प्रत्येक के नाभिक में एक प्रोटॉन होना चाहिए| लेकिन हाइड्रोजन, ड्यूटीरियम एवं ट्राइटियम के नाभिकों के द्रव्यमानों में अनुपात 1 : 2 : 3 है| इसलिए ड्यूटीरियम एवं ट्राइटियम के नाभिकों में प्रोटॉन के अतिरिक्त कुछ उदासीन द्रव्य भी होना चाहिए| इन समस्थानिकों के नाभिकों में विद्यमान उदासीन अनाविष्ट द्रव्य की मात्रा को प्रोटॉन-द्रव्यमान के मात्रकों में व्यक्त करें तो क्रमशः एक एवं दो मात्रकों के लगभग होता है| यह तथ्य इंगित करता है कि परमाणुओं के नाभिकों में प्रोटॉनों के अतिरिक्त विद्यमान रहने वाला यह उदासीन द्रव्य भी एक मूल मात्रक के गुणजों के रूप में ही होता है| इस परिकल्पना की पुष्टि, 1932 में, जेम्स चैडविक द्वारा की गई जिन्होंने देखा कि जब बेरिलियम नाभिकों पर एेल्फ़ा कणों (एेल्फ़ा कण, हीलियम नाभिक होते हैं जिनके विषय में हम अगले अनुभाग में चर्चा करेंगे) की बौछार की जाती है, तो इनसे कुछ उदासीन विकिरण उत्सर्जित होते हैं| यह भी पाया गया कि ये उदासीन विकिरण, हीलियम, कार्बन एवं नाइट्रोजन जैसे हलके नाभिकों से टकराकर उनसे प्रोटॉन बाहर निकालते हैं| उस समय तक ज्ञात एक मात्र उदासीन विकिरण फोटॉन (विद्युत चुंबकीय विकिरण) ही थे| ऊर्जा एवं संवेग संरक्षण के नियमों का प्रयोग करने पर पता चला कि यदि ये उदासीन विकिरण फोटॉनों के बने होते तो इनकी ऊर्जा उन विकिरणों की तुलना में बहुत अधिक होती जो बेरिलियम नाभिकों पर एेल्फ़ा कणों की बौछार से प्राप्त होते हैं| इस समस्या के समाधान का सूत्र, जिसे चैडविक ने संतोषजनक ढंग से हल किया, इस कल्पना में समाहित था कि उदासीन विकिरणों में एक नए प्रकार के उदासीन कण होते हैं जिन्हें न्यूट्रॉन कहते हैं| ऊर्जा एवं संवेग संरक्षण नियमों का उपयोग कर, उन्होंने इस नए कण का द्रव्यमान ज्ञात करने में सफलता प्राप्त की, जिसे प्रोटॉन के द्रव्यमान के लगभग बराबर पाया गया|
अब हम न्यूट्रॉन का द्रव्यमान अत्यधिक यथार्थता से जानते हैं| यह है,
mn = 1.00866 u = 1.6749×10–27 kg (13.3)
न्यूट्रॉन की खोज के लिए चैडविक को 1935 के नोबेल पुरस्कार से सम्मानित किया गया| एक मुक्त प्रोटॉन के विपरीत एक मुक्त न्यूट्रॉन अस्थायी होता है| यह एक प्रोट्रॉन, एक इलेक्ट्रॉन एवं एक प्रतिन्यूट्रिनो (अन्य मूल कण) के रूप में क्षयित हो जाता है| इसकी औसत आयु लगभग 1000 s होती है| तथापि, नाभिक के भीतर यह स्थायी होता है|
अब, नाभिक की संरचना निम्नलिखित पदों एवं संकेत चिह्नों का उपयोग करके समझायी जा सकती है|
Z - परमाणु क्रमांक = प्रोटॉनों की संख्या [13.4(a)]
N - न्यूट्रान संख्या = न्यूट्रॉनों की संख्या [13.4(b)]
A - द्रव्यमान संख्या = Z + N
= न्यूट्रॉनों एवं प्रोटॉनों की कुल संख्या [13.4(c)]
प्रोटॉन एवं न्यूट्रॉन के लिए न्यूक्लियॉन शब्द का भी उपयोग किया जा सकता है| अतः किसी परमाणु में न्यूक्लियॉन संख्या उसकी द्रव्यमान संख्या A होती है|
किसी नाभिकीय प्रजाति या नाभिक को संकेत चिह्न 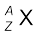 द्वारा प्रदर्शित किया जाता है| जहाँ X उस प्रजाति का रासायनिक चिह्न है| उदाहरण के लिए, स्वर्ण-नाभिक को संकेत
द्वारा प्रदर्शित किया जाता है| जहाँ X उस प्रजाति का रासायनिक चिह्न है| उदाहरण के लिए, स्वर्ण-नाभिक को संकेत 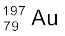 द्वारा व्यक्त करते हैं| इसमें 197 न्यूक्लियॉन होते हैं जिनमें 79 प्रोटॉन एवं 118 न्यूट्रॉन होते हैं|
द्वारा व्यक्त करते हैं| इसमें 197 न्यूक्लियॉन होते हैं जिनमें 79 प्रोटॉन एवं 118 न्यूट्रॉन होते हैं|
अब किसी तत्व के समस्थानिकों की संरचना को सरलता से समझाया जा सकता है| किसी दिए गए तत्व के समस्थानिकों के नाभिकों में प्रोटॉनों की संख्या तो समान होती है, परंतु वे एक-दूसरे से न्यूट्रॉनों की संख्या की दृष्टि से भिन्न होते हैं| ड्यूटीरियम 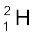 जो हाइड्रोजन का एक समस्थानिक है, इसमें एक प्रोटॉन एवं एक न्यूट्रॉन होता है| इसके दूसरे समस्थानिक ट्राइटियम
जो हाइड्रोजन का एक समस्थानिक है, इसमें एक प्रोटॉन एवं एक न्यूट्रॉन होता है| इसके दूसरे समस्थानिक ट्राइटियम 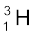 में एक प्रोटॉन एवं दो न्यूट्रॉन होते हैं| तत्व स्वर्ण के 32 समस्थानिक होते हैं जिनकी द्रव्यमान संख्याओं का परास A =173 से A = 204 तक होता है| यह हम पहले ही बता चुके हैं कि तत्वों के रासायनिक गुण उनके इलेक्ट्रॉनिक विन्यास पर निर्भर करते हैं| चूँकि, समस्थानिक परमाणुओं के इलेक्ट्रॉनिक विन्यास समान होते हैं उनका रासायनिक व्यवहार भी एक जैसा होता है और इसलिए उनको आवर्त सारणी में एक ही स्थान पर रखा जाता है|
में एक प्रोटॉन एवं दो न्यूट्रॉन होते हैं| तत्व स्वर्ण के 32 समस्थानिक होते हैं जिनकी द्रव्यमान संख्याओं का परास A =173 से A = 204 तक होता है| यह हम पहले ही बता चुके हैं कि तत्वों के रासायनिक गुण उनके इलेक्ट्रॉनिक विन्यास पर निर्भर करते हैं| चूँकि, समस्थानिक परमाणुओं के इलेक्ट्रॉनिक विन्यास समान होते हैं उनका रासायनिक व्यवहार भी एक जैसा होता है और इसलिए उनको आवर्त सारणी में एक ही स्थान पर रखा जाता है|
एेसे सभी नाभिक जिनकी द्रव्यमान संख्या A समान होती है समभारिक कहलाते हैं| उदाहरणार्थ, नाभिक 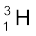 एवं
एवं 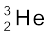 समभारिक हैं| एेसे नाभिक जिनकी न्यूट्रॉन संख्या N समान हो लेकिन परमाणु क्रमांक Z भिन्न हो समन्यूट्रॉनिक कहलाते हैं| उदाहरणार्थ,
समभारिक हैं| एेसे नाभिक जिनकी न्यूट्रॉन संख्या N समान हो लेकिन परमाणु क्रमांक Z भिन्न हो समन्यूट्रॉनिक कहलाते हैं| उदाहरणार्थ, 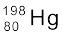 एवं
एवं 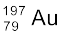 समन्यूट्रॉनिक हैं|
समन्यूट्रॉनिक हैं|
13.3 नाभिक का साइज़
जैसा हमने अध्याय 12 में देखा है, रदरफोर्ड वह अग्रणी वैज्ञानिक थे जिन्होंने परमाणु नाभिक के अस्तित्व की परिकल्पना एवं स्थापना की| रदरफोर्ड के सुझाव पर गीगर एवं मार्सडन ने स्वर्ण के वर्क पर एेल्फ़ा कणों के प्रकीर्णन से संबंधित प्रसिद्ध प्रयोग किया| उनके प्रयोगों से यह स्पष्ट हुआ कि 5.5 MeV गतिज ऊर्जा के एेल्फ़ा कणों की स्वर्ण नाभिकों के निकटस्थ पहुँच की दूरी लगभग 4.0 × 10–14 m है| स्वर्ण की परत से α -कणों के प्रकीर्णन को रदरफोर्ड ने यह मानकर समझाया कि प्रकीर्णन के लिए केवल कूलॉम का प्रतिकर्षण बल ही उत्तरदायी है| चूँकि, धनात्मक आवेश नाभिक में निहित होता है, नाभिक का वास्तविक साइज़ 4.0 × 10–14 m से कम होना चाहिए|
यदि हम 5.5 MeV से अधिक ऊर्जा के α -कण प्रयोग करें तो इनके स्वर्ण नाभिकों के निकटस्थ पहुँच की दूरी और कम हो जाएगी और तब प्रकीर्णन अल्प परास नाभिकीय बलों से प्रभावित होने लगेगा और रदरफोर्ड द्वारा किए गए परिकलनों से प्राप्त मान बदल जाएँगे| रदरफोर्ड के परिकलन एेल्फ़ा कणों एवं स्वर्ण नाभिकों के धनावेश युक्त कणों के बीच लगने वाले शुद्ध कूलॉम प्रतिकर्षण बल पर आधारित हैं| उस दूरी के द्वारा जिस पर रदरफोर्ड के परिकलनों में आने वाले अंतर स्पष्ट होने लगते हैं, नाभिकीय साइज़ों के विषय में निष्कर्ष निकाला जा सकता है|
एेसे प्रकीर्णन प्रयोग करके जिनमें α-कणों के स्थान पर तीव्र गति इलेक्ट्रॉनों की विभिन्न तत्वों के ऊपर बौछार की गई हो, इन तत्वों के नाभिकीय साइज़ अत्यंत परिशुद्धता से ज्ञात किए गए|
यह पाया गया कि A द्रव्यमान संख्या के नाभिक की त्रिज्या है :
R = R0 A1/3 (13.5)
जहाँ R0 = 1.2 × 10–15 m (= 1.2 fm; 1 fm = 10-15m) इसका अर्थ है कि नाभिक का आयतन (जो R3 के अनुक्रमानुपाती है) द्रव्यमान संख्या A के अनुक्रमानुपाती होता है| अतः नाभिक का घनत्व नियत होता है, अर्थात, सभी नाभिकों के लिए इसका मान A पर निर्भर नहीं करता है| विभिन्न नाभिक इस नियत घनत्व के द्रव की बूँद की तरह होते हैं| नाभिकीय द्रव्य का घनत्व 2.3 × 1017 kg m–3 के सन्निकट होता है| सामान्य पदार्थों की तुलना में घनत्व का यह मान बहुत अधिक होता है, जैसे जल के लिए घनत्व केवल 103 kg m–3 ही होता है| इस तथ्य को आसानी से समझा भी जा सकता है, क्योंकि यह हम पहले ही देख चुके हैं कि परमाणु अधिकांशतः भीतर से रिक्त होता है| सामान्य परमाणुओं से बने द्रव्य में बड़ी मात्रा में रिक्त स्थान होता है|
उदाहरण 13.1 लोहे के नाभिक का द्रव्यमान 55.85u एवं A=56 है, इसका नाभिकीय घनत्व ज्ञात कीजिए|
हल
mFe = 55.85
u = 9.27 × 10-26 kg
नाभिकीय घनत्व =  =
= 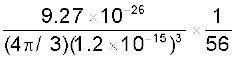
= 2.29 × 1017 kg m–3
न्यूट्रॉन तारे (एक खगोल भौतिकीय पिंड) में पदार्थ का घनत्व इस घनत्व के साथ तुलनीय है| यह दर्शाता है कि इन तारों में द्रव्य इस सीमा तक संपीडित हो गया है कि न्यूट्रॉन तारे स्वयं एक बड़े नाभिक की तरह व्यवहार करते हैं|
13.4 द्रव्यमान-ऊर्जा तथा नाभिकीय बंधन-ऊर्जा
13.4.1 द्रव्यमान-ऊर्जा
आइंस्टाइन ने अपने विशिष्ट आपेक्षिकता सिद्धांत के आधार पर यह दर्शाया कि द्रव्यमान ऊर्जा का ही एक दूसरा रूप है| विशिष्ट आपेक्षिकता सिद्धांत से पहले यह माना जाता था कि किसी अभिक्रिया में द्रव्यमान एवं ऊर्जा अलग-अलग संरक्षित होते हैं| परंतु आइंस्टाइन ने यह दर्शाया कि द्रव्यमान केवल ऊर्जा का दूसरा रूप है और हम द्रव्यमान-ऊर्जा को ऊर्जा के अन्य रूपों, जैसे–गतिज ऊर्जा में, परिवर्तित कर सकते हैं तथा विपरीत प्रक्रम अर्थात ऊर्जा को द्रव्यमान में रूपांतरित करना भी संभव है|
इसके लिए आइंस्टाइन ने जो प्रसिद्ध द्रव्यमान-ऊर्जा समतुल्यता संबंध दिया वह है ः
E = mc2 (13.6)
यहाँ E, द्रव्यमान m के समतुल्य ऊर्जा है एवं c निर्वात में प्रकाश का वेग है जिसका सन्निकट मान 3×108 m s–1 है|
उदाहरण 13.2 1 g पदार्थ के समतुल्य ऊर्जा को परिकलित कीजिए|
हल
ऊर्जा E = 10–3 × ( 3 × 108)2 J
E = 10–3 × 9 × 1016 J = 9 × 1013 J
इस प्रकार, यदि एक ग्राम पदार्थ को भी ऊर्जा में रूपांतरित किया जाए तो इससे ऊर्जा की विशाल मात्रा मुक्त होती है|
आइंस्टाइन के द्रव्यमान-ऊर्जा संबंध की प्रायोगिक पुष्टि, न्यूक्लियॉनों, नाभिकों, इलेक्ट्रॉनों एवं अन्य हाल ही में खोजे गए कणों के बीच होने वाली नाभिकीय अभिक्रियाओं के अध्ययन में हो चुकी है| किसी अभिक्रिया में ऊर्जा संरक्षण नियम से अभिप्राय है कि यदि द्रव्यमान से संबद्ध ऊर्जा को भी परिकलनों में सम्मिलित करें तो प्रारंभिक ऊर्जा अंतिम ऊर्जा के बराबर होती है| यह संकल्पना, नाभिकों की पारस्परिक अन्योन्य क्रियाओं एवं नाभिकीय द्रव्यमानों को समझने के लिए महत्वपूर्ण है| यही अगले कुछ अनुभागों की विषय-वस्तु है|
13.4.2 नाभिकीय बंधन-ऊर्जा
अनुभाग 13.2 में हमने देखा कि नाभिक न्यूट्रॉन एवं प्रोटॉन का बना है| अतः यह अपेक्षित है कि नाभिक का द्रव्यमान, इसमें विद्यमान न्यूट्रॉनों एवं प्रोटॉनों के द्रव्यमानों के कुल योग Σm के बराबर होगा| लेकिन, नाभिकीय द्रव्यमान M, सदैव Σm से कम पाया जाता है| उदाहरण के लिए, आइए 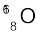 को लें| इसमें 8 प्रोटॉन एवं 8 न्यूट्रॉन हैं| अतः,
को लें| इसमें 8 प्रोटॉन एवं 8 न्यूट्रॉन हैं| अतः,
8 न्यूट्रॉनों का द्रव्यमान = 8 × 1.00866 u
8 प्रोटॉनों का द्रव्यमान = 8 × 1.00727 u
8 इलेक्ट्रॉनों का द्रव्यमान = 8 × 0.00055 u
इसलिए 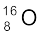 के नाभिक का अपेक्षित द्रव्यमान = 8 × 2.01593 u = 16.12744 u
के नाभिक का अपेक्षित द्रव्यमान = 8 × 2.01593 u = 16.12744 u
द्रव्यमान वर्णक्रममापी के प्रयोगों द्वारा प्राप्त 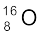 का परमाणु द्रव्यमान 15.99493 u है| इसमें से 8 इलेक्ट्रॉनों का द्रव्यमान (8 × 0.00055 u) घटाने पर
का परमाणु द्रव्यमान 15.99493 u है| इसमें से 8 इलेक्ट्रॉनों का द्रव्यमान (8 × 0.00055 u) घटाने पर 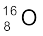 के नाभिक का प्रायोगिक मान 15.99053 u है|
के नाभिक का प्रायोगिक मान 15.99053 u है|
अतः हम पाते हैं कि अॉक्सीजन 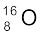 नाभिक का द्रव्यमान, इसके घटकों के कुल द्रव्यमान से 0.13691u कम है| नाभिक के द्रव्यमान एवं इसके घटकों के द्रव्यमान के अंतर ∆M, को द्रव्यमान क्षति कहते हैं, और इसका मान इस प्रकार व्यक्त किया जाता है ः
नाभिक का द्रव्यमान, इसके घटकों के कुल द्रव्यमान से 0.13691u कम है| नाभिक के द्रव्यमान एवं इसके घटकों के द्रव्यमान के अंतर ∆M, को द्रव्यमान क्षति कहते हैं, और इसका मान इस प्रकार व्यक्त किया जाता है ः
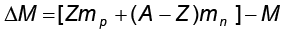 (13.7)
(13.7)
द्रव्यमान-क्षति का अर्थ क्या है? यहीं पर आइंस्टाइन का द्रव्यमान-ऊर्जा समतुल्यता सिद्धांत अपनी भूमिका निभाता है| चूँकि, अॉक्सीजन नाभिक का द्रव्यमान इसके घटकों के द्रव्यमानों के योग (अबंधित अवस्था में 8 प्रोटॉन एवं 8 न्यूट्रॉन का) से कम होता है, अॉक्सीजन नाभिक की समतुल्य ऊर्जा इसके घटकों की समतुल्य ऊर्जाओं के योग से कम होती है| यदि आप अॉक्सीजन नाभिक को 8 प्रोटॉनों एवं 8 न्यूट्रॉनों में विखंडित करना चाहें तो आपको यह अतिरिक्त ऊर्जा,
∆M c2, इस नाभिक को प्रदान करनी होगी| इसके लिए आवश्यक यह ऊर्जा Eb, द्रव्यमान क्षति से निम्नलिखित समीकरण द्वारा संबंधित होती है ः
Eb = ∆ M c2 (13.8)
उदाहरण 13.3 एक परमाणु द्रव्यमान मात्रक के समतुल्य ऊर्जा का मान पहले जूल और फिर MeV में ज्ञात कीजिए| इसका उपयोग करके 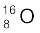 की द्रव्यमान क्षति MeV/c2 में व्यक्त कीजिए|
की द्रव्यमान क्षति MeV/c2 में व्यक्त कीजिए|
हल
1u = 1.6605 × 10–27 kg
इसको ऊर्जा के मात्रकों में परिवर्तित करने के लिए हम इसको c2 से गुणा करते हैं एवं पाते हैं कि इसके
समतुल्य ऊर्जा = 1.6605 × 10–27 × (2.9979 × 108)2 kg m2/s2
= 1.4924 × 10–10 J
= 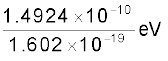
= 0.9315 × 109 eV
= 931.5 MeV
अथवा 1u = 931.5 MeV/c2
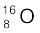 के लिए ∆M = 0.13691 u = 0.13691×931.5 MeV/c2
के लिए ∆M = 0.13691 u = 0.13691×931.5 MeV/c2
= 127.5 MeV/c2
∴ 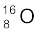 को इसके घटकों में विभाजित करने के लिए आवश्यक ऊर्जा 127.5 MeV/c2 है|
को इसके घटकों में विभाजित करने के लिए आवश्यक ऊर्जा 127.5 MeV/c2 है|
यदि कुछ न्यूट्रॉनों एवं प्रोटॉनों को पास-पास लाकर, निश्चित आवेश एवं द्रव्यमान वाला एक नाभिक बनाया जाए तो इस प्रक्रिया में ∆Eb ऊर्जा मुक्त होगी| यह ऊर्जा ∆Eb नाभिक की बंधन-ऊर्जा कहलाती है| यदि हमें किसी नाभिक के नाभिक-कणों को अलग-अलग करना हो तो हमें इन कणों को कुल ऊर्जा Eb प्रदान करनी होगी| यद्यपि नाभिक को हम इस प्रकार तोड़ नहीं सकते, फिर भी, नाभिक की बंधन-ऊर्जा यह तो बताती ही है कि किसी नाभिक में न्यूक्लियॉन परस्पर कितनी अच्छी तरह से जुड़े हैं| नाभिक के कणों की बंधन शक्ति का एक और अधिक उपयोगी माप बंधन-ऊर्जा प्रति न्यूक्लियॉन, Ebn है; जो कि नाभिक की बंधन-ऊर्जा, Eb एवं इसमें विद्यमान न्यूक्लिअॉनों की संख्या A का अनुपात है|
∆Ebn = ∆Eb /A (13.9)
हम प्रति न्यूक्लियॉन बंधन-ऊर्जा को एेसा मान सकते हैं कि यह किसी नाभिक को इसके न्यूक्लिअॉनों में पृथक्कृत करने के लिए आवश्यक औसत ऊर्जा है|
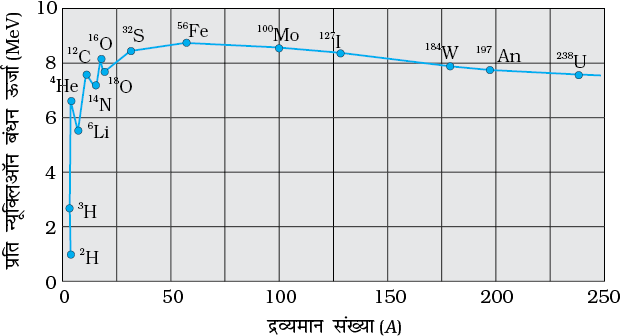
चित्र 13.1 में बहुत से नाभिकों के लिए प्रति न्यूक्लियॉन बंधन ऊर्जा Ebn एवं द्रव्यमान संख्या A में ग्राफ दिखाया गया है| इस ग्राफ में हमें निम्नलिखित लक्षण पर विशेष दृष्टिगोचर होते हैं –
(i) मध्यवर्ती द्रव्यमान संख्याओं ( 30 < A < 170) के लिए, प्रति न्यूक्लियॉन बंधन-ऊर्जा, Ebn, का मान व्यावहारिक रूप में नियत रहता है, अर्थात परमाणु क्रमांक के साथ परिवर्तित नहीं होता है| वक्र A = 56 के लिए लगभग 8.75 MeV का अधिकतम मान एवं A = 238 के लिए 7.6 MeV दर्शाता है|
(ii) हलके नाभिकों (A < 30) एवं भारी नाभिकों (A >170) दोनों के लिए ही Ebn का मान मध्यवर्ती परमाणु क्रमांक के नाभिकों की तुलना में अपेक्षाकृत कम होता है|
इस प्रकार निम्न निष्कर्षों पर पहुँच सकते हैं :
(i) यह बल आकर्षी है तथा प्रति न्यूक्लियॉन कुछ MeV बंधन उत्पन्न करने के लिए पर्याप्त प्रबल है|
(ii) 30 < A < 170 के परास में बंधन-ऊर्जा की अचरता इस तथ्य का परिणाम है कि नाभिकीय बल लघु परासी बल होते हैं| बड़े नाभिक के भीतर स्थित किसी न्यूक्लियॉन पर विचार कीजिए| यह अपने पास-पड़ोस के केवल उन न्यूक्लिअॉनों से प्रभावित होगा जो इसके नाभिकीय बल के परिसर में आते हैं| यदि कोई अन्य न्यूक्लियॉन इस विशिष्ट न्यूक्लियॉन के नाभिकीय बल के परिसर से अधिक दूरी पर है, तो यह विचाराधीन नाभिक की बंधन-ऊर्जा को तनिक भी प्रभावित नहीं करेगा| यदि किसी नाभिक के नाभिकीय बल के परिसर में अधिकतम p न्यूक्लियॉन हो सकते हों, तो इसकी बंधन-ऊर्जा p के अनुक्रमानुपाती होगी| माना कि किसी नाभिक की बंधन-ऊर्जा pk है, जहाँ k एक नियतांक है जिसकी विमाएँ वही हैं जो ऊर्जा की होती हैं| अब यदि हम न्यूक्लियॉनों की संख्या बढ़ाकर A का मान बढ़ाएँ, तो इससे नाभिक के भीतर न्यूक्लियॉनों की बंधन-ऊर्जा प्रभावित नहीं होगी| क्योंकि, किसी भी बड़े नाभिक में अधिकांश न्यूक्लियॉन इसके भीतर रहते हैं तथा पृष्ठ की अपेक्षा, नाभिक की बंधन-ऊर्जा पर A की वृद्धि का कुल प्रभाव नगण्य रहता है| अतः प्रति न्यूक्लियॉन बंधन-ऊर्जा नियत रहती है और इसका सन्निकट मान pk के बराबर होता है| नाभिकों का वह गुण जिसके कारण कोई नाभिक केवल अपने निकट के नाभिकों को ही प्रभावित करता है, नाभिकीय बलों का संतृप्ति गुण कहलाता है|
(iii) एक अत्यधिक भारी नाभिक, जैसे A = 240, की प्रति न्यूक्लियॉन बंधन-ऊर्जा, A = 120 के नाभिक की तुलना में कम होती है| अतः, यदि A = 240 का कोई नाभिक, A = 120 के दो नाभिकों में टूटता है तो, इनमें न्यूक्लियॉन अधिक दृढ़ता से परिबद्ध होंगे| यह इंगित करता है कि इस प्रक्रिया में ऊर्जा विमुक्त होगी| यह विखंडन द्वारा ऊर्जा विमुक्त होने की महत्वपूर्ण संभावना को अभिव्यक्त करता है जिसके विषय में हम अनुभाग 13.7.1 में चर्चा करेंगे|
(iv) कल्पना कीजिए कि दो हलके नाभिक (A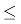 10) संलयित होकर एक भारी नाभिक बनाते हैं| संलयन द्वारा बने इस भारी नाभिक की प्रति न्यूक्लियॉन बंधन-ऊर्जा, हलके नाभिकों की प्रति न्यूक्लियॉन बंधन ऊर्जा से अधिक होती है| इसका अर्थ यह हुआ कि अंतिम निकाय में कण प्रारंभिक निकाय की तुलना में अधिक दृढ़ता से बंधित हैं| यहाँ संलयन की इस प्रक्रिया में भी ऊर्जा विमुक्त होगी| यही सूर्य की ऊर्जा का स्रोत है जिसके विषय में हम अनुभाग 13.7.3 में चर्चा करेंगे|
10) संलयित होकर एक भारी नाभिक बनाते हैं| संलयन द्वारा बने इस भारी नाभिक की प्रति न्यूक्लियॉन बंधन-ऊर्जा, हलके नाभिकों की प्रति न्यूक्लियॉन बंधन ऊर्जा से अधिक होती है| इसका अर्थ यह हुआ कि अंतिम निकाय में कण प्रारंभिक निकाय की तुलना में अधिक दृढ़ता से बंधित हैं| यहाँ संलयन की इस प्रक्रिया में भी ऊर्जा विमुक्त होगी| यही सूर्य की ऊर्जा का स्रोत है जिसके विषय में हम अनुभाग 13.7.3 में चर्चा करेंगे|
13.5 नाभिकीय बल
वह बल जो परमाणु में इलेक्ट्रॉनों की गति नियंत्रित करता है हमारा सुपरिचित कूलॉम बल है| अनुभाग 13.4 में हमने देखा कि औसत द्रव्यमान के नाभिक के लिए प्रति न्यूक्लियॉन बंधन-ऊर्जा लगभग 8 MeV है जो परमाणु की बंधन-ऊर्जा की तुलना में बहुत अधिक है| अतः नाभिक में कणों को परस्पर बाँधे रखने के लिए एक भिन्न प्रकार के शक्तिशाली आकर्षण बल की आवश्यकता है| यह बल इतना अधिक शक्तिशाली होना चाहिए कि (धनावेशित) प्रोटॉनों के बीच लगे प्रतिकर्षण बलों से अधिक प्रभावी होकर प्रोटॉनों एवं न्यूट्रॉनों दोनों को नाभिक के सूक्ष्म आयतन में बाँधे रख सके| हम यह पहले ही देख चुके हैं कि प्रति न्यूक्लियॉन बंधन ऊर्जा की अचरता को इन बलों की लघु परासी प्रकृति से समझा जा सकता है| नाभिकीय बंधन बलों के कुछ अभिलक्षणों को संक्षेप में नीचे दिया गया है| यह ज्ञान 1930 से 1950 के बीच किए गए विभिन्न प्रयोगों द्वारा प्राप्त हुआ है|
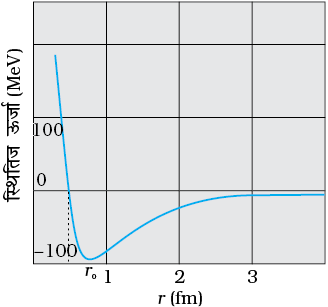
चित्र 13.2 एक नाभिकीय युग्म की स्थितिज ऊर्जा उनके बीच की दूरी के फलन के रूप में| r0 से अधिक दूरी होने परबल आकर्षण बल होता है एवं r0 से कम दूरी पर तीव्र प्रतिकर्षण बल| आकर्षण बल सर्वाधिक प्रबल तब होता है जब नाभिकों के बीच की दूरी r0 होती है|
(i) नाभिकीय बल, आवेशों के बीच लगने वाले कूलॉम बल एवं द्रव्यमानों के बीच लगने वाले गुरुत्वाकर्षण बल की तुलना में अत्यधिक शक्तिशाली होता है| नाभिकीय बंधन बल को, नाभिक के भीतर प्रोटॉनों के बीच लगने वाले कूलॉम प्रतिकर्षण बल पर आधिपत्य करना होता है| यह इसीलिए संभव हो पाता है, क्योंकि नाभिकीय बल कूलॉम बलों की तुलना में अत्यधिक प्रबल होते हैं| गुरुत्वाकर्षण बल तो कूलॉम बल की तुलना में भी अत्यंत दुर्बल होता है|
(ii) न्यूक्लिअॉनों के बीच दूरी बढ़ाकर कुछ फेम्टोमीटर से अधिक करने पर उनके बीच लगने वाला नाभिकीय बल तेज़ी से घटकर शून्य हो जाता है| इस कारण, औसत अथवा बड़े साइज़ के नाभिकों में ‘बलों की संतृप्तता’ की स्थिति आ जाती है जिसके परिणामस्वरूप प्रति न्यूक्लियॉन बंधन-ऊर्जा नियत हो जाती है| दो नाभिकों की स्थितिज ऊर्जा और उनके बीच की दूरी में संबंध दर्शाने वाला एक अपरिष्कृत आरेख चित्र 13.2 में दर्शाया गया है| लगभग 0.8 fm की दूरी r0 पर स्थितिज ऊर्जा का मान न्यूनतम होता है| इसका अर्थ यह हुआ कि यदि नाभिकों के बीच दूरी 0.8 fm से अधिक होती है तो ये बल आकर्षण बल होते हैं और 0.8 fm से कम दूरियों के लिए ये प्रतिकर्षण बल होते हैं|
(iii) न्यूट्रॉन-न्यूट्रॉन, न्यूट्रॉन-प्रोटॉन एवं प्रोटॉन-प्रोटॉन के बीच लगने वाले नाभिकीय बल लगभग समान परिमाण के होते हैं| नाभिकीय बल विद्युत आवेशों पर निर्भर नहीं करते|
कूलॉम के नियम अथवा न्यूटन के गुरुत्वीय नियम की भाँति नाभिकीय बलों का कोई सरल गणितीय रूप नहीं है|
* ∆N क्षयित नाभिकों की संख्या है, अतः इसका मान सदैव धनात्मक होता है| dN, N में परिवर्तन है और इसका कोई भी चिह्न हो सकता है| यहाँ यह ऋणात्मक है क्योंकि, मूल N नाभिकों में ∆N क्षयित हो जाते हैं और (N–∆N) शेष रहते हैं|
13.6 रेडियोएेक्टिवता
रेडियोएेक्टिवता की खोज ए.एच. बैकेरल ने सन्् 1896 में संयोगवश की| यौगिकों को दृश्य प्रकाश से विकीर्णित करके उनकी प्रतिदीप्ति एवं स्फुरदीप्ति का अध्ययन करते हुए बैकेरल ने एक रोचक परिघटना देखी| यूरेनियम-पोटैशियम सल्फेट के कुछ टुकड़ों पर दृश्य प्रकाश डालने के बाद उसने उनको काले कागज़ में लपेट दिया| इस पैकेट और फ़ोटोग्राफ़िक प्लेट के बीच एक चाँदी का टुकड़ा रखा| इसी प्रकार कई घंटे तक रखने के बाद जब फ़ोटोग्राफ़िक प्लेट को डेवेलप किया गया तो यह पाया गया कि यह प्लेट काली पड़ चुकी थी| यह किसी एेसी चीज़ के कारण हुआ होगा जो यौगिक से उत्सर्जित हुई होगी तथा काले कागज़ और चाँदी दोनों को भेद कर फ़ोटोग्राफ़िक प्लेट तक पहुँच गई होगी|
बाद में किए गए प्रयोगों ने दर्शाया कि रेडियोएेक्टिवता एक नाभिकीय परिघटना है जिसमें अस्थायी नाभिक क्षयित होता है| इसे रेडियोएेक्टिव क्षय कहते हैं| प्रकृति में तीन प्रकार के रेडियोएेक्टिव क्षय होते हैं ः
(i) α-क्षय, जिसमें हीलियम नाभिक ( ) उत्सर्जित होते हैं,
) उत्सर्जित होते हैं,
(ii) β-क्षय, जिसमें इलेक्ट्रॉन अथवा पॉजीट्रॉन (एेसे कण जिसका द्रव्यमान तो इलेक्ट्रॉन के बराबर ही होता है पर आवेश ठीक इलेक्ट्रॉन के विपरीत होता है) उत्सर्जित होते हैं|
(iii) γ-क्षय, जिसमें उच्च ऊर्जा (100 keV अथवा अधिक) फोटॉन उत्सर्जित होते हैं|
इनमें प्रत्येक प्रकार के क्षय पर आगामी उपअनुभागों में विचार किया जाएगा|
13.6.1 रेडियोएेक्टिव क्षयता का नियम
किसी रेडियोएेक्टिव नमूने में जिसमें α, β अथवा γ-क्षय हो रहा हो, यह पाया जाता है कि एकांक समय में क्षयित होने वाले नाभिकों की संख्या, नमूने में विद्यमान कुल नाभिकों की संख्या के अनुक्रमानुपाती होती है| यदि दिए गए नमूने में नाभिकों की संख्या N हो और ∆t समय में ∆N नाभिक क्षयित हो रहे हों तो
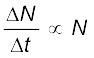
अथवा, ∆N/∆t = λN (13.10)
जहाँ λ रेडियोेएेक्टिव क्षय-स्थिरांक अथवा विघटन-स्थिरांक है|
∆t समय में दिए गए नमूने* में नाभिकों की संख्या में हुआ परिवर्तन है dN = – ∆N| अतः, (जब ∆t → 0) तो N में परिवर्तन की दर है–
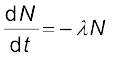
अथवा, 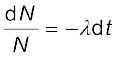
इस समीकरण का दोनों ओर समाकलन करने पर,
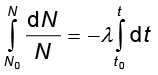 (13.11)
(13.11)
अथवा ln N − ln N0 = −λ (t – t0) (13.12)
यहाँ N0, किसी यादृच्छिक क्षण t0 पर रेडियोएेक्टिव नाभिकों की संख्या है| t0 = 0 रखकर समीकरण (13.12) को पुनर्व्यवस्थित करने पर,
ln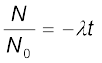 (13.13)
(13.13)
जिससे हमें प्राप्त होता है,
N(t) = N0 e −λt (13.14)
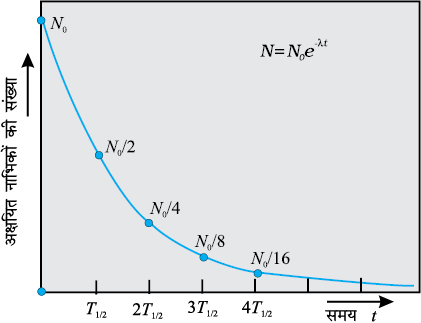
चित्र 13.3 रेडियोएेक्टिव प्रजातियों का चरघातांकी क्षय| प्रत्येक T1/2 समय के पश्चात दी गई प्रजाति की संख्या आधी रह जाती है|
मैरी स्क्लाडोवका क्यूरी (1867-1934)

मैरी स्क्लाडोवका क्यूरी (1867-1934) पोलैंड में जन्मी|
भौतिकविज्ञानी एवं रसायनज्ञ दोनों रूपों में पहचान मिली| 1896 में हेनरी बैकेरल द्वारा रेडियोएेक्टिवता की खोज ने मैरी और उनके पति पियरे क्यूरी को उनके अनुसंधानों एवं विश्लेषणों के लिए प्रेरित किया, जिसके फलस्वरूप तत्वों– रेडियम एवं पोलोनियम– का पृथक्करण संभव हुआ| वह प्रथम वैज्ञानिक थीं जिन्हें दो नोबेल पुरस्कार प्राप्त हुए ः पहला 1903 में भौतिकी के लिए और दूसरा 1911 में रसायनविज्ञान के लिए|
ध्यान देने योग्य बात यह है कि विद्युत बल्ब एेसे किसी चर घातांकी क्षय नियम का पालन नहीं करता| यदि हम 1000 बल्बों की आयु (वह काल विस्तृति जिसके बाद वे फ्यूज़ होंगे) का परीक्षण करें तो हम यह आशा करेंगे कि ये सभी लगभग एक साथ क्षयित (फ्यूज़) हो जाएँगे| रेडियो नाभिकों का क्षय एक पूर्णतः भिन्न नियम, उस रेडियोएेक्टिव-क्षयता नियम के अनुसार होता है, जो समीकरण (13.14) द्वारा व्यक्त किया गया है|
किसी नमूने की क्षयता दर R प्रति एकांक समय में क्षयित होने वाले नाभिकों की संख्या होती है| माना कि dt समयांतराल में क्षयित होने वाले नाभिकों की संख्या ∆N है, तो dN = – ∆N| धनात्मक राशि R की निम्न व्याख्या होती हैः
R = –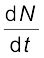
समीकरण (13.14) का अवकलन करने पर,
R = –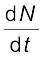 = λN0 e −λt
= λN0 e −λt
अथवा R = R0 e –λt (13.15)
यह रेडियोएेक्टिव क्षयता नियम के समान है [क्योंकि समी. (13.15) का समाकलन करने पर समी. (13.14) प्राप्त होगा] स्पष्टतः R0 = λN0,
t = 0 पर क्षयता दर है| किसी निश्चित समय t पर क्षयता दर R, उस समय अक्षयित नाभिकों की संख्या N से निम्न रूप में संबंधित होती हैः
R = λN (13.16)
रेडियोएेक्टिव नाभिकों की संख्या की तुलना में, किसी नमूने की क्षयता दर अधिक प्रायोगिक मापन राशि है तथा इसका एक निश्चित नाम सक्रियता (एेक्टिवता) है| इसका SI मात्रक बैकेरल (प्रतीक Bq) है जो रेडियोएेक्टिवता के अन्वेषक हेनरी बैकेरल की स्मृति में निश्चित किया गया है|
1 बैकेरल का अर्थ 1 क्षय प्रति सेकंड है| एक दूसरा मात्रक क्यूरी (प्रतीक Ci) भी सामान्य प्रचलन में है जो SI मात्रक Bq से निम्न रूप से संबंधित हैः
1 क्यूरी = 1 Ci = 3.7 × 1010 क्षय प्रति सेकंड = 3.7 × 1010 Bq
विभिन्न रेडियो-नाभिकों की क्षयता दर में अधिक भिन्नता होती है| इस गुण को अर्ध-आयु के आधार पर मापा जा सकता है| किसी रेडियो-नाभिक की अर्ध-आयु (T1/2) वह समय है, जिसमें इसकी संख्या, प्रारंभिक संख्या (माना कि N0) की आधी (अर्थात् N0/2) रह जाय| समी.
(13.14) में, समय t = T1/2 तथा N = N0/2 रखने परः
T1/2 = 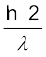
= 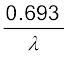 (13.17)
(13.17)
समी. (13.16) के अनुसार, स्पष्टतः यदि संख्या N0, T1/2 समय में आधी हो जाती है तो सक्रियता R0 भी इसी समय में आधी रह जाएगी|
एक और संबंधित मापदंड औसत-आयु (1966.png) है| इसका मान भी समी. (13.14) से प्राप्त किया जा सकता है| किसी समयांतराल t से t + ∆t में क्षयित नाभिक R(t)∆t = (λN0e–λt∆t) हैं| इनमें से सभी t समय तक जीवित रहते हैं| अतः इन सभी नाभिकों का कुल जीवन t λN0e–λt होगा| यह स्पष्ट है कि कुछ नाभिकों का जीवन काल कम तथा कुछ नाभिकों का जीवन काल अधिक होता है| अतः औसत आयु का मान प्राप्त करने के लिए उक्त व्युक्ति का हमें कुल
समय 0 से  तक के लिए योग (अथवा समाकलन) कर समय t = 0 पर उपलब्ध नाभिकों की संख्या N0 से भाग देना होगा| अतः
तक के लिए योग (अथवा समाकलन) कर समय t = 0 पर उपलब्ध नाभिकों की संख्या N0 से भाग देना होगा| अतः
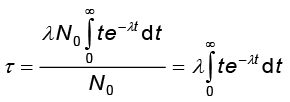
इस समाकलन को करने पर
τ = 1/λ
प्राप्त होगा|
उपरोक्त परिणामों को हम संक्षेप में इस प्रकार प्रकट कर सकते हैंः
T1/2 = 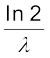 = τ ln 2 (13.18)
= τ ln 2 (13.18)
एेसे रेडियोएेक्टिव तत्व (जैसे कि ट्राइटियम एवं प्लूटोनियम) जिनकी अर्ध-आयु विश्व की आयु (लगभग 15 अरब वर्ष) की तुलना में बहुत कम है, काफी समय पहले ही विघटित हो चुके हैं तथा प्रकृति में उपलब्ध नहीं हैं| हालाँकि, इनका नाभिकीय अभिक्रियाओं में अप्राकृतिक रूप से उत्पादन किया जा सकता है|
उदाहरण 13.4 क्षयित हो रहे 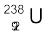 की, α-क्षय के लिए अर्ध-आयु 4.5 ×109 वर्ष है|
की, α-क्षय के लिए अर्ध-आयु 4.5 ×109 वर्ष है| 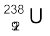 के 1 g नमूने की एेक्टिवता क्या है?
के 1 g नमूने की एेक्टिवता क्या है?
हल
T1/2 = 4.5 × 109 y
= 4.5 × 109 y × 3.16 × 107 s/y
= 1.42 × 1017 s
किसी समस्थानिक के 1 kmol में आवोगाद्रो संख्या के बराबर परमाणु होते हैं| अतः 1g, 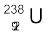 में परमाणुओं की संख्या,
में परमाणुओं की संख्या, 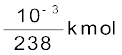 × 6.025 × 1026 परमाणु/kmol
× 6.025 × 1026 परमाणु/kmol
= 25.3 × 1020 है|
∴ क्षयता दर R है,
R = λN
= 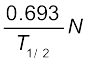 =
= 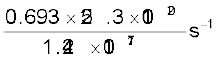
= 1.23 × 104 s–1
= 1.23 × 104 Bq
उदाहरण 13.5 β-क्षय द्वारा, ट्राइटियम की अर्ध-आयु 12.5 वर्ष है| 25 वर्ष बाद शुद्ध ट्राइटियम के एक नमूने का कितना अंश अविघटित रहेगा?
हल परिभाषा के अनुसार 12.5 वर्ष बाद ट्राइटियम के नमूने का ½ भाग बचेगा| अगले 12.5 वर्ष में इस आधे का फिर आधा यानी ¼ भाग बचेगा| अतः 25 साल बाद शुद्ध ट्राइटियम के किसी नमूने का ¼ अविघटित भाग रहेगा|
13.6.2 एेल्फ़ा-क्षय
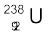 का
का 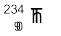 में क्षय एेल्फ़ा-क्षय का एक प्रचलित उदाहरण है| इस प्रक्रिया में हीलियम नाभिक (
में क्षय एेल्फ़ा-क्षय का एक प्रचलित उदाहरण है| इस प्रक्रिया में हीलियम नाभिक (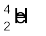 ) उत्सर्जित होता हैः
) उत्सर्जित होता हैः
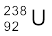 →
→ 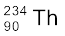 +
+  (13.19)
(13.19)
एेल्फ़ा-क्षय में, उत्पादित विघटनज नाभिक की द्रव्यमान-संख्या क्षय होने वाले मूल नाभिक की तुलना में 4 कम होती है तथा परमाणु क्रमांक 2 कम होता है| सामान्यतः किसी मूल नाभिक 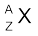 के विघटनज नाभिक
के विघटनज नाभिक 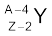 में रूपांतरण को इस प्रकार व्यक्त करते हैं
में रूपांतरण को इस प्रकार व्यक्त करते हैं
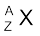 →
→ 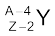 +
+  (13.20)
(13.20)
आइंस्टाइन के द्रव्यमान-ऊर्जा समतुल्यता संबंध [समी. (13.6)] तथा ऊर्जा संरक्षण से यह स्पष्ट है कि एेसा स्वतः क्षय केवल क्षय उत्पादों का कुल द्रव्यमान प्रारंभिक नाभिक के द्रव्यमान से कम होने की स्थिति में ही संभव है| द्रव्यमान में यह अंतर उत्पादों की गतिज ऊर्जा के रूप में अवतरित होता है| नाभिकीय द्रव्यमानों की सूची से यह ज्ञात किया जा सकता है कि 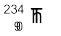 तथा
तथा 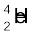 का कुल द्रव्यमान वास्तव में
का कुल द्रव्यमान वास्तव में 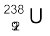 के द्रव्यमान से कम होता है|
के द्रव्यमान से कम होता है|
प्रारंभिक द्रव्यमान-ऊर्जा एवं क्षय उत्पादों की कुल द्रव्यमान-ऊर्जा का अंतर इस प्रक्रिया का Q–मान अथवा विघटनज ऊर्जा कहलाता है| एेल्फ़ा-क्षय में
Q = (mX – mY – mHe) c2 (13.21)
ऊर्जा का यह मान इस प्रक्रिया में जनित कुल गतिज ऊर्जा अथवा उत्पादों की कुल गतिज ऊर्जा (यदि प्रारंभिक नाभिक X स्थिर हो) भी है| स्पष्टतः किसी ऊष्माक्षेपी प्रक्रिया (जैसे कि एेल्फ़ा-क्षय) के लिए Q > 0|
13.6.3 बीटा-क्षय
बीटा-क्षय में किसी नाभिक से एक इलेक्ट्रॉन (β––क्षय) अथवा एक पॉजिट्रॉन (β+–क्षय) का स्वतः उत्सर्जन होता है| β––क्षय तथा β+–क्षय के सामान्य उदाहरण निम्न हैंः
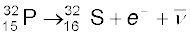 (13.22)
(13.22)
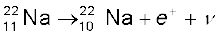 (13.23)
(13.23)
ये क्षय समी. (13.14) तथा (13.15) के अनुसार ही हैं, जिससे कि यह प्रागुक्ति नहीं की जा सकती कि कौन सा नाभिक क्षयित होगा| परंतु इस क्षय को अर्ध-आयु (T1/2) से दर्शाया जा सकता है| उदाहरण के लिए, उपरोक्त क्षयों के लिए अर्ध-आयु क्रमशः 14.3 दिन तथा 2.6 वर्ष हैं|
β––क्षय में इलेक्ट्रॉन के उत्सर्जन के साथ ही एक एंटीन्यूट्रिनो (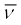 ) का भी उत्सर्जन होता है| तथा β+ –क्षय में पॉजिट्रॉन के साथ न्यूट्रिनो (ν) का उत्सर्जन होता है| न्यूट्रिनो इलेक्ट्रॉन की तुलना में बहुत कम द्रव्यमान (संभवतः शून्य) वाले अनावेशित कण होते हैं| ये अन्य कणों के साथ केवल क्षीण अन्योन्य क्रिया करते हैं| ये बिना क्रिया किये पदार्थ की बहुत बड़ी मात्रा (पृथ्वी भी) को पार कर सकते हैं| यही कारण है कि इनका संसूचन बहुत कठिन है|
) का भी उत्सर्जन होता है| तथा β+ –क्षय में पॉजिट्रॉन के साथ न्यूट्रिनो (ν) का उत्सर्जन होता है| न्यूट्रिनो इलेक्ट्रॉन की तुलना में बहुत कम द्रव्यमान (संभवतः शून्य) वाले अनावेशित कण होते हैं| ये अन्य कणों के साथ केवल क्षीण अन्योन्य क्रिया करते हैं| ये बिना क्रिया किये पदार्थ की बहुत बड़ी मात्रा (पृथ्वी भी) को पार कर सकते हैं| यही कारण है कि इनका संसूचन बहुत कठिन है|
β––तथा β+–दोनों ही क्षयों में द्रव्यमान संख्या A नहीं बदलती है| β––क्षय में नाभिक का परमाणु क्रमांक Z, 1 अधिक हो जाता है, जबकि β+–क्षय में 1 कम हो जाता है| β––क्षय में मूल नाभिकीय प्रक्रिया न्यूट्रॉन का प्रोटॉन में रूपांतरण हैः
n → p + e– + 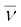 (13.24)
(13.24)
जबकि β+–क्षय में प्रोटॉन का न्यूट्रॉन में रूपांतरण होता हैः
p → n + e+ + 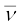 (13.25)
(13.25)
प्रोटॉन का द्रव्यमान, न्यूट्रॉन के द्रव्यमान से कम है, अतः प्रोटॉन का न्यूट्रॉन में क्षय [समी. (13.25)] केवल नाभिक के अंदर ही संभव है, जबकि न्यूट्रॉन का प्रोटॉन में क्षय मुक्त अवस्था में भी संभव है [समी. (13.24)]|
13.6.4 गामा-क्षय
परमाणु के समान, नाभिक में भी विभिन्न ऊर्जा स्तर होते हैं– अनउत्तेजित अवस्था तथा उत्तेजित अवस्थाएँ| हालाँकि इनके ऊर्जा के मानों में अत्यधिक विभिन्नता होती है| परामाण्विक ऊर्जा स्तरों का कोटिमान eV का होता है, जबकि नाभिकीय ऊर्जा स्तरों में ऊर्जाओं का अंतर MeV के कोटिमान का होता है| जब कोई उत्तेजित नाभिक निम्न उत्तेजित अवस्था अथवा अनुत्तेजित अवस्था में संक्रमित होता है तो नाभिक के दोनों ऊर्जा स्तरों के अंतर के समान ऊर्जा का फोटॉन उत्सर्जित होता है| यही गामा-क्षय कहलाता है| यह ऊर्जा (MeV), कठोर X–किरणों के परिसर से कम तंरगदैर्घ्य वाले विकिरणों से संबंधित होती है|
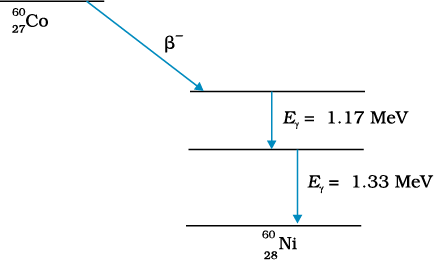
सामान्यतः किसी गामा किरण का उत्सर्जन, एेल्फ़ा अथवा बीटा-क्षय में विघटनज नाभिक का उत्तेजित अवस्था में रहने की अवस्था में होता है| उत्तेजित नाभिक अनुत्तेजित अवस्था में आने की प्रक्रिया में एक फोटॉन अथवा एक से अधिक फोटॉनों (क्रमवार संक्रमण की अवस्था में) का उत्सर्जन करते हैं| 1.17 MeV तथा 1.33 MeV ऊर्जाओं की गामा किरणों के क्रमवार उत्सर्जन का सामान्य उदाहरण 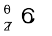 नाभिक के β––क्षय द्वारा
नाभिक के β––क्षय द्वारा 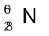 नाभिक में क्षयित होने की प्रक्रिया में प्रदर्शित होता है|
नाभिक में क्षयित होने की प्रक्रिया में प्रदर्शित होता है|
13.7 नाभिकीय ऊर्जा
चित्र 13.1 में दर्शाये गए प्रति न्यूक्लिअॉन बंधन-ऊर्जा Ebn वक्र में A = 30 एवं A= 170 के बीच एक लंबा सपाट भाग है| इस भाग में प्रति न्यूक्लिअॉन बंधन-ऊर्जा लगभग अचर (8.0MeV) है| हलके नाभिकों, A > 30, वाले भाग एवं भारी नाभिकों, A > 170, वाले भाग में, जैसा हम पहले ही देख चुके हैं, प्रति न्यूक्लिअॉन बंधन-ऊर्जा 8.0 MeV से कम है| यदि बंधन-ऊर्जा अधिक हो तो उस बंधित निकाय जैसे नाभिक का कुल द्रव्यमान कम होगा| परिणामस्वरूप यदि कोई कम कुल बंधन-ऊर्जा वाला नाभिक किसी अधिक बंधन-ऊर्जा वाले नाभिक में रूपांतरित हो तो कुल ऊर्जा विमुक्त होगी| किसी भारी नाभिक के दो या दो से अधिक माध्यमिक द्रव्यमान खंडों (विखंडन) अथवा हलके नाभिकों का किसी भारी नाभिक में संयोजन (संलयन) की प्रक्रिया में एेसा ही होता है|
कोयले एवं पेट्रोलियम जैसे पारंपरिक ऊर्जा स्रोतों में ऊष्माक्षेपी रासायनिक अभिक्रियाएँ होती हैं| यहाँ विमुक्त होने वाली ऊर्जा इलेक्ट्रॉन वोल्ट की कोटि की होती है| जबकि किसी नाभिकीय प्रक्रिया में, MeV कोटि की ऊर्जा विमुक्त होती है| अतः द्रव्य की समान मात्रा के लिए, रासायनिक स्रोतों की अपेक्षा नाभिकीय स्रोत लाखों गुना ऊर्जा विमुक्त करते हैं| उदाहरण के लिए, 1 kg यूरेनियम के विखंडन से लगभग 1014J ऊर्जा प्राप्त होती है, जबकि 1 kg कोयले के दहन से 107J ऊर्जा प्राप्त होती है|
13.7.1 विखंडन
प्राकृतिक रेडियोएेक्टिव क्षयों के अलावा नाभिकों पर अन्य नाभिकीय कणों जैसे प्रोटॉन, न्यूट्रॉन, एेल्फा कण आदि के प्रकार से होने वाली नाभिकीय प्रक्रियाओं पर ध्यान देने से नई संभावनाएँ बनती हैं|
विखंडन एक महत्वपूर्ण न्यूट्रॉन-प्रेरक नाभिकीय प्रक्रिया है| विखंडन के उदाहरणतः जब किसी यूरेनियम समस्थानिक 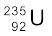 पर न्यूट्रॉन से प्रहार कराया जाता है तो वह दो माध्यमिक द्रव्यमान वाले नाभिकीय खंडों में विखंडित हो जाता है ः
पर न्यूट्रॉन से प्रहार कराया जाता है तो वह दो माध्यमिक द्रव्यमान वाले नाभिकीय खंडों में विखंडित हो जाता है ः
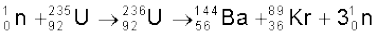 (13.26)
(13.26)
इसी क्रिया में माध्यमिक द्रव्यमान वाले नाभिकों के भिन्न युग्म भी उत्पन्न हो सकते हैं ः
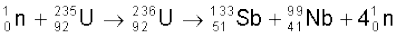 (13.27)
(13.27)
एक अन्य उदाहरण है ः
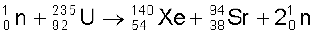
(13.28)
ये विखंडित उत्पाद रेडियोएेक्टिव नाभिक होते हैं और इनमें तब तक β-क्षय का क्रम चलता रहता है जब तक कि अंत में स्थायी खंड प्राप्त न हो जाएँ|
यूरेनियम जैसे नाभिक की विखंडन अभिक्रिया में निर्मुक्त ऊर्जा (Q -मान) प्रति विखंडित नाभिक 200 MeV की कोटि की होती है| इसका आकलन हम निम्नवत करते हैं ः
माना कि एक नाभिक का A = 240 है और यह A = 120 के दो खंडों में विखंडित होता है| तब
A = 240 नाभिक के लिए Ebn लगभग 7.6 MeV है (चित्र 13.1 देखें)|
A = 120 वाले विखंडित नाभिक के लिए Ebn लगभग 8.5 MeV है|
प्रति न्यूक्लियॉन बंधन-ऊर्जा की लब्धि लगभग 0.9 MeV है|
अतः बंधन-ऊर्जा में कुल लब्धि 240×0.9 अथवा 216 MeV है|
विखंडन की घटनाओं की विघटन ऊर्जा पहले क्षय-उत्पादों तथा न्यूट्रॉनों की गतिज ऊर्जा के रूप में संलग्नित होती है| अंत में यह आसपास के द्रव्य को हस्तांतरित होकर ऊष्मा के रूप में परिणित हो जाती है| नाभिकीय रिएक्टरों में नाभिकीय विखंडन ऊर्जा से विद्युत उत्पादन होता है| परमाणु बम में विमुक्त होने वाली बृहत ऊर्जा अनियंत्रित नाभिकीय विखंडन से ही उत्पन्न होती है| अगले अनुभाग में हम कुछ विस्तार से यह चर्चा करेंगे कि नाभिकीय रिएक्टर कैसे कार्य करता है|
13.7.2 नाभिकीय रिएक्टर
समीकरणों (13.26) से (13.28) में वर्णित विखंडन से एक अति महत्वपूर्ण सत्य प्रतीत होता है| विखंडन क्रिया में एक अतिरिक्त न्यूट्रॉन की उत्पत्ति होती है| प्रति यूरेनियम विखंडन में औसतन 2.5 न्यूट्रॉनों की उत्पत्ति होती है| यह एक अनुपात है क्योंकि कुछ विखंडन घटनाओं में 2 न्यूट्रॉनों तथा कुछ में 3 न्यूट्रॉनों की उत्पत्ति होती है| ये अतिरिक्त न्यूट्रॉन अन्य विखंडन क्रियाओं की शुरुआत कर सकते हैं तथा और भी अधिक न्यूट्रॉनों की उत्पत्ति हो सकती है| इससे एक शृंखला अभिक्रिया की संभावना बनती है| यह विचार सर्वप्रथम एनरिको फर्मी ने रखा था| यदि इस शृंखला-अभिक्रिया को समुचित रूप से नियंत्रित किया जाए तो हमें एक स्थायी ऊर्जा निर्गत हो सकती है| नाभिकीय रिएक्टर में यही होता है| यदि शृंखला अभिक्रिया अनियंत्रित हो जाये तो इससे विखंडनकारी एवं विनाशकारी ऊर्जा निर्गत हो सकती है, जैसा कि किसी नाभिकीय बम में होता है|
परमाणु ऊर्जा के क्षेत्र में भारत के बढ़ते कदम
भारत में परमाणु ऊर्जा कार्यक्रम की शुरुआत डॉ. होमी जहाँगीर भाभा (1909 – 1966) के नेतृत्व में लगभग स्वतंत्रता प्राप्ति के साथ ही की गई| एक प्रारंभिक, एेतिहासिक उपलब्धि पहले भारतीय नाभिकीय रिएक्टर (अप्सरा नामक) की रचना एवं निर्माण था जिसने 4 अगस्त 1956 से अपना कार्य शुरू किया| इसमें संवर्धित यूरेनियम को ईंधन और जल को मंदक की तरह इस्तेमाल किया गया था| इसके बाद दूसरी बड़ी घटना 1960 में बना कनाडा इंडिया रिएक्टर(CIRUS) था| 40 MW के इस रिएक्टर में प्राकृतिक यूरेनियम ईंधन की तरह एवं भारी जल मंदक की तरह इस्तेमाल किया गया था| अप्सरा एवं साइरस ने मूल एवं प्रायोगिक नाभिकीय विज्ञान के विभिन्न क्षेत्रों में विस्तृत शोध को प्रोत्साहित किया| कार्यक्रम के पहले दो दशकों की विशिष्ट उपलब्धियों में एक था ट्रॉम्बे में स्वदेशी प्लूटोनियम संयंत्र की रचना एवं निर्माण, जिसने भारत में ईंधन पुनर्संसाधन तकनीकी (रिएक्टर के मुक्त शेष ईंधन से उपयोगी विखंडनीय एवं उर्वर नाभिकीय सामग्री को अलग करना) का मार्ग प्रशस्त किया| बाद में जो अन्य रिएक्टर शोध के लिए शुरू किए गए, उनमें शामिल हैं– एरलिना, पूर्णिमा (I, II एवं III), ध्रुव एवं कामिनी| कामिनी देश का पहला बड़ा शोध रिएक्टर है जिसमें U-233 को ईंधन की तरह इस्तेमाल किया गया है| जैसा नाम से स्पष्ट है शोध-रिएक्टर का प्राथमिक उद्देश्य शक्ति जनन नहीं है, वरन नाभिकीय विज्ञान एवं तकनीकी के विभिन्न पक्षों पर शोध के लिए सुविधा प्रदान करना है| शोध रिएक्टर विभिन्न समस्थानिकों के उत्पादन के भी श्रेष्ठ स्रोत हैं जिनके विभिन्न क्षेत्रों–उद्योग, औषधि, कृषि आदि में उपयोग हैं|
कार्यक्रम का मुख्य उद्देश्य शुरू से ही यह रहा है कि देश के सामाजिक एवं आर्थिक विकास के लिए सुरक्षित एवं विश्वसनीय विद्युत शक्ति प्रदान की जाए और नाभिकीय तकनीकी के सभी क्षेत्रों में आत्मनिर्भर बना जाए| पचास के दशक के शुरुआती वर्षों में, भारत में परमाण्विक खनिजों को ढूँढ़ने का जो कार्य हुआ, उससे यह संकेत मिले कि यहाँ यूरेनियम के भंडार तो बहुत सीमित हैं, पर थोरियम के भंडार पर्याप्त मात्रा में हैं| उसके अनुसार ही हमारे देश ने नाभिकीय शक्ति जनन की एक तीन चरणों में पूरी होने वाली योजना अपनायी| पहले चरण में प्राकृतिक यूरेनियम को ईंधन के रूप में एवं भारी जल को मंदक के रूप में प्रयुक्त किया जाना है| रिएक्टर के अपशिष्ट को पुनर्संसाधित करने पर प्राप्त प्लूटोनियम-239, दूसरे चरण में तीव्र रिएक्टर में ईंधन का काम करता है| इन रिएक्टरों को तीव्र प्रजनक रिएक्टर इसलिए कहते हैं क्योंकि इनमें शृंखला प्रक्रिया को बनाए रखने के लिए तीव्र न्यूट्रॉनों का उपयोग होता है (अतः मंदक की आवश्यकता नहीं होती) और ये शक्ति जनन के अतिरिक्त, जिस तरह का ईंधन खर्च करते हैं, उससे अधिक विखंडनशील पदार्थों (प्लूटोनियम) को जन्म भी देते हैं| तीसरा चरण, जो दीर्घकालिक योजना के हिसाब से सर्वाधिक महत्त्वपूर्ण है, एेसे तीव्र प्रजनक रिएक्टरों के इस्तेमाल पर आधारित है जो थोरियम-232 को विखंडनशील यूरेनियम-233 में बदलेंगे और फिर इनके लिए विशेष रूप से बनाए गए शक्ति संयंत्रों में इस्तेमाल किए जाएँगे|
अभी भारत कार्यक्रम के दूसरे चरण से गुजर रहा है और थोरियम के उपयोग संबंधी तीसरे चरण के लिए भी काफ़ी कार्य हो चुका है| देश ने खनिज अनुसंधान एवं उत्खनन| ईंधन निर्माण, भारी जल उत्पादन, रिएक्टर की रचना, निर्माण एवं प्रचालन, तथा ईंधन पुनर्संसाधन आदि, संश्लिष्ट तकनीकों पर प्रभुत्व प्राप्त कर लिया है| संपीडित भारी जल रिएक्टर(PHWRs) जो देश में विभिन्न स्थानों पर बनाए गए हैं, पहले चरण की पूर्णता का संकेत देते हैं| भारत अब अपनी आवश्यकता से अधिक भारी जल का उत्पादन कर रहा है| रिएक्टरों की रचना एवं प्रचालन दोनों के संबंध में विस्तृत सुरक्षा प्रबंध तथा रेडियो विकिरणों से बचाव संबंधी प्रामाणिक निर्देशों का सख्ती से पालन, भारतीय परमाणु ऊर्जा कार्यक्रम की पहचान है|
हालांकि, किसी शृंखला अभिक्रिया को पोषित करने में एक और दुविधा है, जैसा कि यहाँ वर्णित है| प्रयोगों से हमें ज्ञात है कि मंद न्यूट्रॉनों (तापीय न्यूट्रॉन) द्वारा तीव्र न्यूट्रॉनों की अपेक्षा 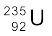 में विखंडन की ज्यादा प्रायिकता है| विखंडन में निकले तीव्र न्यूट्रॉन अन्य विखंडन प्रक्रिया करने की अपेक्षा बाहर भी निकल सकते हैं|
में विखंडन की ज्यादा प्रायिकता है| विखंडन में निकले तीव्र न्यूट्रॉन अन्य विखंडन प्रक्रिया करने की अपेक्षा बाहर भी निकल सकते हैं|
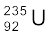 के विख्ांडन में उत्पादित न्यूट्रॉन की औसत ऊर्जा 2 MeV होती है| ये न्यूट्रॉन जब तक कि इनका मंदन न किया जाए, यूरेनियम नाभिकों से क्रिया किए बिना ही रिएक्टर से बाहर निकल जाते हैं| यूरेनियम नाभिकों से इन तीव्र न्यूट्रॉनों के लिए शृंखला क्रिया (chain reaction) को बनाए रखने में प्रयुक्त विखंडनीय पदार्थ की बहुत अधिक मात्रा की आवश्यकता होती है| तीव्र न्यूट्रॉनों को हलके न्यूट्रॉनों के साथ प्रत्यास्थ संघट्ट द्वारा मंदित किया जाता है| वास्तव में, चैडविक के प्रयोगों ने दर्शाया कि हाइड्रोजन के साथ प्रत्यास्थ टक्कर में न्यूट्रॉन लगभग स्थिर हो जाते हैं तथा समस्त ऊर्जा प्रोटॉन द्वारा ले ली जाती है| यह स्थिति वैसी ही है जैसा कि किसी गतिमान काँच की गोली की अन्य स्थिर समान गोली के साथ आमने-सामने की टक्कर| अतः रिएक्टरों में, तीव्र न्यूट्रॉनों को मंदित करने के लिए विखंडनीय नाभिकों के साथ हलके नाभिकों [जिन्हें अवमंदक (moderator) कहते हैं] का प्रयोग किया जाता है| प्रायः प्रयुक्त होने वाले अवमंदक जल, भारी जल (D2O) तथा ग्रैफाइट हैं| भाभा परमाणु अनुसंधान केंद्र (BARC), मुंबई के अप्सरा रिएक्टर में अवमंदक के रूप में जल का प्रयोग होता है| शक्ति उत्पादन के लिए प्रयुक्त भारत के अन्य रिएक्टरों में अवमंदक के रूप में भारी जल का उपयोग होता है|
के विख्ांडन में उत्पादित न्यूट्रॉन की औसत ऊर्जा 2 MeV होती है| ये न्यूट्रॉन जब तक कि इनका मंदन न किया जाए, यूरेनियम नाभिकों से क्रिया किए बिना ही रिएक्टर से बाहर निकल जाते हैं| यूरेनियम नाभिकों से इन तीव्र न्यूट्रॉनों के लिए शृंखला क्रिया (chain reaction) को बनाए रखने में प्रयुक्त विखंडनीय पदार्थ की बहुत अधिक मात्रा की आवश्यकता होती है| तीव्र न्यूट्रॉनों को हलके न्यूट्रॉनों के साथ प्रत्यास्थ संघट्ट द्वारा मंदित किया जाता है| वास्तव में, चैडविक के प्रयोगों ने दर्शाया कि हाइड्रोजन के साथ प्रत्यास्थ टक्कर में न्यूट्रॉन लगभग स्थिर हो जाते हैं तथा समस्त ऊर्जा प्रोटॉन द्वारा ले ली जाती है| यह स्थिति वैसी ही है जैसा कि किसी गतिमान काँच की गोली की अन्य स्थिर समान गोली के साथ आमने-सामने की टक्कर| अतः रिएक्टरों में, तीव्र न्यूट्रॉनों को मंदित करने के लिए विखंडनीय नाभिकों के साथ हलके नाभिकों [जिन्हें अवमंदक (moderator) कहते हैं] का प्रयोग किया जाता है| प्रायः प्रयुक्त होने वाले अवमंदक जल, भारी जल (D2O) तथा ग्रैफाइट हैं| भाभा परमाणु अनुसंधान केंद्र (BARC), मुंबई के अप्सरा रिएक्टर में अवमंदक के रूप में जल का प्रयोग होता है| शक्ति उत्पादन के लिए प्रयुक्त भारत के अन्य रिएक्टरों में अवमंदक के रूप में भारी जल का उपयोग होता है|
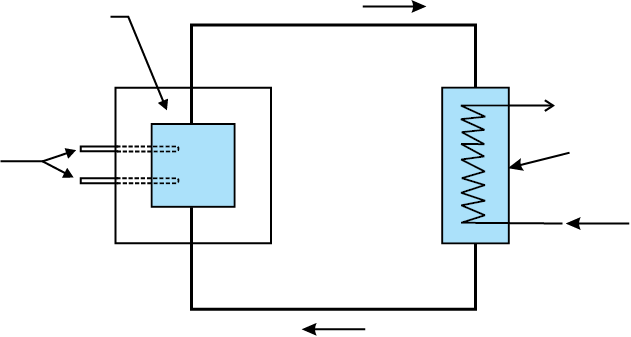
चित्र 13.5 तापीय न्यूट्रॉन विखंडन पर आधारित किसी नाभिकीय रिएक्टर की सरलीकृत रूपरेखा
अवमंदक के उपयोग के कारण, किसी स्तर पर निकले न्यूट्रॉनों के द्वारा विखंडनों की संख्या का उसके पिछले स्तर पर निकले न्यूट्रॉनों के द्वारा विखंडनों की संख्या के साथ अनुपात, K का मान एक से अधिक हो सकता है| इस अनुपात को गुणन कारक (multiplication factor) कहते हैं| यह रिएक्टर में न्यूट्रॉनों की वृद्धि दर को मापता है| K = 1, के लिए रिएक्टर की प्रवृत्ति क्रांतिक कहलाती है जो स्थिर शक्ति उत्पादन की प्रवृत्ति के लिए एेच्छिक है| K का मान एक से अधिक होने पर क्रिया दर तथा रिएक्टर की शक्ति में चरघातांकी (exponentially) क्रम में वृद्धि होती है| K का मान एक की संख्या के आसपास न होने पर रिएक्टर अतिक्रांतिक हो जायेगा तथा रिएक्टर में विस्फोट भी हो सकता है| सन् 1986 में यूक्रेन के चेर्नोबिल रिएक्टर में हुआ विस्फोट इस दुखद तथ्य का स्मरण कराता है कि नाभिकीय रिएक्टर में कोई दुर्घटना कितनी विनाशकारी हो सकती है|
क्रिया दर नियंत्रण कैडमियम जैसे न्यूट्रॉन-अवशोषक पदार्थ से बनी नियंत्रक छड़ों (control rods) द्वारा किया जाता है| नियंत्रक छड़ों के अतिरिक्त रिएक्टरों में रक्षक छड़ों को भी प्रयुक्त किया जाता है| इन रक्षक छड़ों को आवश्यकता पड़ने पर रिएक्टर में निर्विष्ट करा कर K का मान शीघ्रता से एक से कम किया जा सकता है|
प्राकृतिक रूप में पाये जाने वाले यूरेनियम में प्रचुर 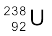 समस्थानिक अ-विखंडनीय होता है| जब इसमें किसी न्यूट्रॉन का ग्रहण (capture) होता है, तो अत्यंत रेडियोएेक्टिव प्लूटोनियम का उत्पादन निम्न क्रियाओं से होता हैः
समस्थानिक अ-विखंडनीय होता है| जब इसमें किसी न्यूट्रॉन का ग्रहण (capture) होता है, तो अत्यंत रेडियोएेक्टिव प्लूटोनियम का उत्पादन निम्न क्रियाओं से होता हैः

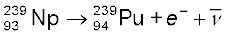 (13.29)
(13.29)
प्लूटोनियम में मंद न्यूट्रॉनों के प्रहार से विखंडन हो सकता है| चित्र 13.5 में तापीय न्यूट्रॉन विखंडन पर आधारित किसी नाभिकीय रिएक्टर का सरलीकृत प्रारूप दर्शाया गया है| रिएक्टर की क्रोड नाभिकीय विखंडन का क्षेत्र है| इसमें उपयुक्त सांचे हुए रूप में ईंधन तत्व रहते हैं| यह ईंधन, प्राकृतिक रूप से पाये जाने वाले यूरेनियम की अपेक्षा 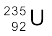 में प्रचुर बहुल यूरेनियम भी हो सकता है| क्रोड में न्यूट्रॉनों को मंद करने के लिए मंदक (moderator) लगे होते हैं| दरार में से छूटने (leakage) को रोकने के लिए क्रोड एक परावर्तक (reflector) से घिरी होती है| एक समुचित शीतलक द्वारा विखंडन में निकली ऊर्जा (उष्मा) को निरंतर हटाया जाता है| विखंडित रेडियोएेक्टिव उत्पादों के पलायन को रोकने के लिए पात्र लगे होते हैं| इस सारी व्यवस्था से हानिकारक विकिरणोें को बाहर न आने देने के लिए एक कवच का उपयोग किया जाता है| न्यूट्रॉनों के अवशोषण की उच्च क्षमता वाली छड़ों (जैसे कि कैडमियम की बनी) के उपयोग से रिएक्टर को बंद किया जा सकता है| शीतलक से उष्मा एक कार्यकारी द्रव्य को स्थानान्तरित की जाती है जिससे कि भाप का उत्पादन होता है| इस भाप से टर्बाइन को घुमाकर विद्युत उत्पादन होता है| किसी अन्य शक्ति रिएक्टर की भांति ही नाभिकीय रिएक्टर से काफी मात्रा में निरर्थक उत्पाद निकलते हैं| परन्तु नाभिकीय निरर्थकों के निराकरण में विशेष ध्यान देना होता है क्योंकि ये रेडियोएेक्टिव तथा हानिकारक होते हैं| रिएक्टर के संचालन, उनके रख-रखाव तथा व्ययित ईंधन के लिए विस्तृत सुरक्षा प्रबंध किये जाते हैं| भारतीय परमाणु ऊर्जा कार्यक्रम में ये सुरक्षा प्रबंध विशिष्ट हैं| रेडियोएेक्टिव अपशिष्टों को कम सक्रिय तथा अल्पजीवी द्रव्यों में परिवर्तित करने की संभावनाओं के अध्ययन के लिए एक समुचित उपयुक्त योजना के विकास पर कार्य चल रहा है|
में प्रचुर बहुल यूरेनियम भी हो सकता है| क्रोड में न्यूट्रॉनों को मंद करने के लिए मंदक (moderator) लगे होते हैं| दरार में से छूटने (leakage) को रोकने के लिए क्रोड एक परावर्तक (reflector) से घिरी होती है| एक समुचित शीतलक द्वारा विखंडन में निकली ऊर्जा (उष्मा) को निरंतर हटाया जाता है| विखंडित रेडियोएेक्टिव उत्पादों के पलायन को रोकने के लिए पात्र लगे होते हैं| इस सारी व्यवस्था से हानिकारक विकिरणोें को बाहर न आने देने के लिए एक कवच का उपयोग किया जाता है| न्यूट्रॉनों के अवशोषण की उच्च क्षमता वाली छड़ों (जैसे कि कैडमियम की बनी) के उपयोग से रिएक्टर को बंद किया जा सकता है| शीतलक से उष्मा एक कार्यकारी द्रव्य को स्थानान्तरित की जाती है जिससे कि भाप का उत्पादन होता है| इस भाप से टर्बाइन को घुमाकर विद्युत उत्पादन होता है| किसी अन्य शक्ति रिएक्टर की भांति ही नाभिकीय रिएक्टर से काफी मात्रा में निरर्थक उत्पाद निकलते हैं| परन्तु नाभिकीय निरर्थकों के निराकरण में विशेष ध्यान देना होता है क्योंकि ये रेडियोएेक्टिव तथा हानिकारक होते हैं| रिएक्टर के संचालन, उनके रख-रखाव तथा व्ययित ईंधन के लिए विस्तृत सुरक्षा प्रबंध किये जाते हैं| भारतीय परमाणु ऊर्जा कार्यक्रम में ये सुरक्षा प्रबंध विशिष्ट हैं| रेडियोएेक्टिव अपशिष्टों को कम सक्रिय तथा अल्पजीवी द्रव्यों में परिवर्तित करने की संभावनाओं के अध्ययन के लिए एक समुचित उपयुक्त योजना के विकास पर कार्य चल रहा है|
13.7.3 नाभिकीय संलयन-तारों में ऊर्जा जनन
चित्र 13.1 में दर्शाया गया बंधन-ऊर्जा वक्र यह भी दर्शाता है कि यदि दो हलके नाभिक मिलकर एक अपेक्षाकृत बड़ा नाभिक बनाएँ तो ऊर्जा निर्मुक्त होती है| इस प्रक्रिया को नाभिकीय संलयन कहते हैं| इस तरह की ऊर्जा विमोचक अभिक्रियाओं के कुछ उदाहरण नीचे दिए गए हैं ः
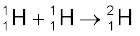 + e+ + ν + 0.42 MeV [13.29(a)]
+ e+ + ν + 0.42 MeV [13.29(a)]
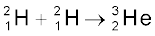 + n + 3.27 MeV [13.29(b)]
+ n + 3.27 MeV [13.29(b)]
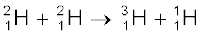 + 4.03 MeV [13.29(c)]
+ 4.03 MeV [13.29(c)]
अभिक्रिया 13.29 (a) में दो प्रोटॉन मिलकर एक ड्यूट्रॉन एवं एक पॉज़िट्रॉन बनाते हैं और इस प्रक्रिया में 0.42 MeV ऊर्जा निकलती है| अभिक्रिया 13.29 (b) में दो ड्यूट्रॉन मिलकर हीलियम का हलका समस्थानिक बनाते हैं| अभिक्रिया 13.29 (c) में दो ड्यूट्रॉन मिलकर एक ट्रीटियम एवं एक प्रोटॉन बनाते हैं| संलयन के लिए दो नाभिकों का इतने अधिक पास आना आवश्यक है जिससे कि उनके बीच आकर्षित लघु-परासीय नाभिकीय बल कार्य कर सके| हालाँकि दोनों नाभिक धनात्मक आवेशित हैं, अतः उनके बीच कूलॉम प्रतिकर्षण होगा| अतः इनमें कूलॉम अवरोध पार करने के लिए समुचित ऊर्जा होनी आवश्यक है| इस कूलॉम अवरोध की ऊँचाई आवेशों एवं अन्योन्यक्रिया गत नाभिकों की त्रिज्याओं पर निर्भर करती है| उदाहरण के लिए, यह आसानी से दर्शाया जा सकता है कि दो प्रोटॉनों के लिए यह अवरोधतुंगता (barrier height) लगभग 400 keV है| अधिक आवेशधारी नाभिकों के लिए अवरोधतुंगता और भी अधिक होगी| किसी प्रोटॉन गैस में प्रोटॉनों द्वारा कूलॉम अवरोध को पार करने के लिए पर्याप्त ऊर्जा 3×109 K ताप पर प्राप्त हो सकती है| इस ताप का परिकलन, सूत्र (3/2)k T = K में K का मान 400 keV रखने पर किया जा सकता है|
ऊर्जा की उपयोगी मात्रा उत्पन्न करने के लिए नाभिकीय संलयन स्थूल-द्रव्य में होना चाहिए| आवश्यकता बस इस बात की है कि द्रव्य का ताप तब तक बढ़ाया जाए जब तक कि इसके कण मात्र अपनी तापीय गति के कारण, कूलॉम अवरोध को पार न कर जाएँ| इस प्रक्रिया को ताप नाभिकीय संलयन कहते हैं|
तारों के अंतः पटल में निर्गत ऊर्जा का स्रोत ताप नाभिकीय संलयन है| सूर्य के क्रोड का ताप लगभग 1.5 ×107 K है, जो कि औसत ऊर्जा के कणों के संलयन के लिए आवश्यक अनुमानित ताप से काफी कम है| स्पष्टतः सूर्य में होने वाली संलयन प्रक्रियाओं में औसत ऊर्जाओं से बहुत अधिक ऊर्जा वाले प्रोटॉन भाग लेते हैं|
अतः ताप नाभिकीय संलयन बहुत उच्च ताप एवं दाब पर ही हो सकता है और ताप एवं दाब की एेसी स्थितियाँ केवल तारों के अंतरंग में ही उपलब्ध हैं| तारों में ऊर्जा जनन ताप-नाभिकीय संलयन के माध्यम से ही होता है|
सूर्य में होने वाली संलयन अभिक्रिया एक बहुचरण प्रक्रिया है जिसमें हाइड्रोजन हीलियम में बदलती है| अतः सूर्य के क्रोड में हाइड्रोजन ईंधन है| प्रोटॉन-प्रोटॉन (p – p) चक्र जिसके द्वारा यह घटित होता है, निम्नलिखित अभिक्रियाओं के समुच्चय द्वारा व्यक्त किया जा सकता है|
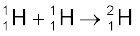 + e+ + ν + 0.42 MeV (i)
+ e+ + ν + 0.42 MeV (i)
e+ + e– → γ + γ + 1.02 MeV (ii)
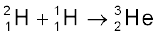 + γ + 5.49 MeV (iii)
+ γ + 5.49 MeV (iii)
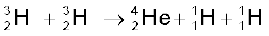 + 12.86 MeV (iv) (13.30)
+ 12.86 MeV (iv) (13.30)
चौथी अभिक्रिया होने के लिए यह आवश्यक है कि पहली तीन अभिक्रियाएँ दो-दो बार हों और इस प्रकार दो हलके हीलियम नाभिक मिलकर सामान्य हीलियम का एक नाभिक बनाएँ| अगर हम 2(i) + 2(ii) + 2(iii) +(iv) पर विचार करें तो कुल प्रभाव होगा,
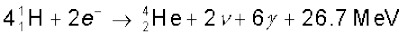
या 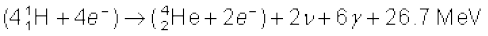 (13.31)
(13.31)
अतः चार हाइड्रोजन परमाणु मिलकर एक 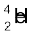 परमाणु बनाते हैं और इस प्रक्रिया में 26.7 MeV ऊर्जा निर्मुक्त होती है|
परमाणु बनाते हैं और इस प्रक्रिया में 26.7 MeV ऊर्जा निर्मुक्त होती है|
किसी तारे के अंतः पटल में केवल हीलियम का ही निर्माण नहीं होता| जैसे-जैसे क्रोड में हाइड्रोजन (हीलियम में बदल कर) कम होती है, क्रोड ठंडा होने लगता है| इससे तारा अपने गुरुत्व के कारण संकुचित होता है जिससे क्रोड का ताप बढ़ जाता है| यदि क्रोड का ताप 108K तक बढ़ जाये तो संलयन की क्रिया पुनः होने लगेगी, पर इस बार हीलियम कार्बन में परिवर्तित होगी| इस प्रकार की प्रक्रिया में संलयन द्वारा बड़े द्रव्यमान संख्या वाले तत्वों का जनन हो सकता है| परन्तु बंधन-ऊर्जा वक्र (चित्र 13.1) के शीर्ष पर स्थित भारी तत्वों का निर्माण इस प्रक्रिया से नहीं हो सकता|
सूर्य की आयु लगभग 5×109 वर्ष है तथा यह अनुमान लगाया जाता है कि सूर्य को और 5 अरब वर्षों तक बनाये रखने के लिए आवश्यक हाइड्रोजन उपलब्ध है| इसके पश्चात्, हाइड्रोजन का जलना रुक जाएगा तथा सूर्य ठंडा होने लगेगा| इससे सूर्य अपने गुरुत्व के कारण संकुचित होने लगेगा जिससे सूर्य की क्रोड का ताप बढ़ेगा| इससे सूर्य का बाहरी आवरण फैलने लगेगा जिससे सूर्य एक लाल दानव (red giant) में परिवर्तित हो जाएगा|
नाभिकीय विध्वंस
एक यूरेनियम नाभिक के विखंडन में लगभग 0.9×235 MeV (≈200 MeV) ऊर्जा विमुक्त होती है, यदि लगभग 50kg 2295.png का प्रत्येक नाभिक विखंडित हो जाए तो लगभग 4 × 1015J ऊर्जा उत्पन्न होगी| यह ऊर्जा 20,000 टनTNT के समतुल्य है जो एक महा विस्फोट के लिए पर्याप्त है| बड़ी मात्रा में नाभिकीय ऊर्जा का अनियंत्रित निर्मुक्त परमाणु विस्फोट कहलाता है| 6 अगस्त 1945 को युद्ध में पहली बार एक परमाणु युक्ति का उपयोग किया गया| अमेरिका ने जापान के शहर हिरोशिमा पर एक परमाणु बम गिराया| विस्फोट 20,000 टन TNT के समतुल्य था| रेडियोएेक्टिव उत्पादों ने एक क्षण में 3,43,000 निवासियों वाले शहर के 10 वर्ग किलोमीटर क्षेत्र को नष्ट कर दिया| इनमें 66,000 मर गए, 69,000 घायल हुए, शहर की 67% से अधिक इमारतें तहस-नहस हो गईं|
संलयन अभिक्रियाओं के लिए आवश्यक उच्च ताप विखंडन बम द्वारा उत्पन्न किया जा सकता है| 1954 में 10 मेगा टन TNT की विस्फोटक क्षमता के समतुल्य महाविस्फोट का परीक्षण किया गया| ये बम जिनमें हाइड्रोजन के समस्थानिकों, ड्यूटीरियम एवं ट्रीटियम का संलयन होता है, हाइड्रोजन बम कहलाते हैं| एेसा माना जाता है कि इतने शक्तिशाली नाभिकीय हथियार स्थापित कर दिए गए हैं जो महज एक बटन दबाने पर कई बार पृथ्वी से जीवन का सफाया कर सकते हैं| एेसे नाभिकीय विध्वंस से न सिर्फ पृथ्वी का वर्तमान जीवन नष्ट हो जाएगा, बल्कि इसके रेडियोएेक्टिव अपशिष्ट आने वाले समय के लिए भी पृथ्वी पर जीवन पनपने योग्य नहीं रहने देंगे| सैद्धांतिक गणनाओं के आधार पर जो परिदृश्य उभरकर आता है उसकी प्रागुक्ति (prediction) यह है कि एक लंबा नाभिकीय शीत युग प्रारंभ हो जाएगा क्योंकि रेडियोएेक्टिव अपशिष्ट बादल की तरह वायुमंडल में तैरेंगे और सूर्य से पृथ्वी की ओर आने वाले सभी विकिरणों को अवशोषित कर लेंगे|
13.7.4 नियंत्रित ताप नाभिकीय संलयन
किसी तारे में होने वाली ताप-नाभिकीय प्रक्रिया का रूपांतरण एक ताप-नाभिकीय युक्ति से किया जाता है| किसी नियंत्रित संलयन रिएक्टर का उद्देश्य नाभिकीय ईंधन को 108K ताप के परास में गरम कर स्थायी शक्ति जनन करना होता है| इस ताप पर ईंधन धनात्मक आयनों तथा इलेक्ट्रॉनों (प्लाज्मा) का मिश्रण होता है| चूंकि इस ताप को बनाये रखने के लिए कोई वस्तु उपलब्ध नहीं है, अतः इस ताप को बनाये रखना एक चुनौती है| भारत सहित विश्व के कई देश इस संबंध में युक्तियों के विकास में प्रयासरत हैं| इन प्रयासों के सफल होने पर, संभावना है कि संलयन रिएक्टर समाज को लगभग अनियमित शक्ति प्रदान कर सकेंगे|
उदाहरण 13.7 निम्नलिखित प्रश्नों के उत्तर दीजिए :
(a) क्या नाभिकीय अभिक्रियाओं के समीकरण (जैसा कि भाग 13.7 में दिए हैं) रासायनिक समीकरण (उदाहरण के लिए 2H2 + O2→ 2 H2O) के रूप में संतुलित हैं? यदि नहीं तो किस रूप में दोनों ओर समीकरण संतुलित होंगे|
(b) यदि प्रोटॉनों और न्यूट्रॉनों की संख्या, प्रत्येक नाभिकीय अभिक्रिया में संरक्षित रहती है, किसी नाभिकीय अभिक्रिया में किस प्रकार द्रव्यमान, ऊर्जा मे (या इसका उलटा) बदलता है?
(c) सामान्य विचार है कि केवल नाभिकीय क्रिया में ही द्रव्यमान-ऊर्जा एक दूसरे में बदले जा सकते हैं जबकि रासायनिक क्रिया में यह कभी नहीं होता है| यह कहना असत्य है| समझाइए|
हल
(a) किसी रासायनिक अभिक्रिया के संतुलित होने की स्थिति में कि अभिक्रिया के समीकरण के दोनों ओर सभी तत्वों के परमाणुओं की संख्या समान होती है| किसी रासायनिक अभिक्रिया में परमाणुओं के मूल संयोजन में परिवर्तन मात्र होता है| परंतु किसी नाभिकीय अभिक्रिया में तत्वांतरण भी हो सकता है| अतः नाभिकीय अभिक्रिया में प्रत्येक तत्व के परमाणुओं की संख्या का संरक्षित होना आवश्यक नहीं है| हालाँकि, नाभिकीय अभिक्रिया में प्रोटॉनों तथा न्यूट्रॉनों दोनों की संख्याएँ पृथक रूप से संरक्षित रहती हैं| [वास्तव में, अत्यधिक ऊर्जा के परिमंडल में यह कथन भी सुनिश्चित सत्य नहीं है| वस्तुतः कुल आवेश तथा कुल ‘बेरियॉन संख्या’ संरक्षित रहते हैं| हम इस विषय पर यहाँ आगे और विचार नहीं करेंगे|] नाभिकीय अभिक्रियाओं [जैसे कि समीकरण (13.26)] में समीकरण के दोनों ओर प्रोटॉनों की संख्याएँ तथा न्यूट्रॉनों की संख्याएँ पृथक-पृथक रूप में समान हैं|
(b) हम जानते हैं कि नाभिक की बंधन-ऊर्जा का नाभिक के द्रव्यमान में ऋणात्मक योगदान (द्रव्यमान क्षति) होता है| चूँकि किसी नाभिकीय अभिक्रिया में प्रोटॉनों तथा न्यूट्रॉनों दोनों की संख्याएँ संरक्षित रहती हैं, अतः अभिक्रिया के दोनों ओर न्यूट्रॉनों तथा प्रोटॉनों का कुल विराम द्रव्यमान (rest mass) समान होता है| परंतु किसी नाभिकीय अभिक्रिया में बायीं ओर के नाभिकों की कुल बंधन-ऊर्जा अभिक्रिया के दायीं ओर के नाभिकों की कुल बंधन-ऊर्जा के समान होना आवश्यक नहीं है| इन बंधन-ऊर्जाओं का अंतर नाभिकीय अभिक्रिया में अवशोषित होने वाली अथवा निकलने वाली ऊर्जा के रूप में प्रकट होता है| चूँकि बंधन-ऊर्जा द्रव्यमान में योगदान देती है, अतः हम कहते हैं कि किसी नाभिकीय अभिक्रिया में दोनों ओर के कुल द्रव्यमानों का अंतर ऊर्जा के रूप में परिवर्तित हो जाता है (या इसके विपरीत ऊर्जा कुल द्रव्यमान के अंतर के रूप में परिवर्तित हो जाती है|)| इस रूप में नाभिकीय अभिक्रिया द्रव्यमान-ऊर्जा के अंतःरूपांतरण का एक उदाहरण है|
(c) द्रव्यमान-ऊर्जा के अंतःरूपांतरण की दृष्टि से, सिद्धांततः एक रासायनिक अभिक्रिया नाभिकीय अभिक्रिया के समरूप है| किसी रासायनिक अभिक्रिया में अवशोषित अथवा निकलने वाली ऊर्जा अभिक्रिया के दोनों ओर के परमाणुओं तथा अणुओं की रासायनिक (नाभिकीय नहीं) बंधन ऊर्जाओं के अंतर को स्पष्ट करती है| चूँकि रासायनिक बंधन-ऊर्जा भी किसी परमाणु अथवा अणु के कुल द्रव्यमान में ऋणात्मक योगदान (द्रव्यमान-क्षति) को दर्शाती है, इसलिए हम निष्कर्ष निकाल सकते हैं कि किसी रासायनिक अभिक्रिया मे दोनों ओर के परमाणुओं तथा अणुओं के कुल द्रव्यमानों का अंतर ऊर्जा के रूप में परिवर्तित हो जाता है या ऊर्जा कुुल द्रव्यमानों के अंतर के रूप में परिवर्तित होकर समाविष्ट हो जाती है| हालाँकि, किसी रासायनिक अभिक्रिया में संलग्न द्रव्यमान क्षतियों का परिमाण नाभिकीय क्रिया में संलग्न द्रव्यमान क्षतियों की तुलना में कई लाख गुना कम होता है| सामान्य रूप में यही धारणा है कि एेसा प्रतीत होता है| (जो सत्य नहीं है) कि किसी रासायनिक अभिक्रिया में कोई द्रव्यमान-ऊर्जा का अंतःरूपांतरण नहीं होता|
सारांश
1. प्रत्येक परमाणु में एक नाभिक होता है| नाभिक धनावेशित होता है| नाभिक की त्रिज्या परमाणु की त्रिज्या से 104गुना छोटी होती है| परमाणु का 99.9% से अधिक द्रव्यमान नाभिक में समाहित होता है|
2. परमाणुओं के स्तर पर द्रव्यमान, परमाणु द्रव्यमान इकाइयों (u) में मापे जाते हैं| परिभाषा के अनुसार 1 परमाणु द्रव्यमान इकाई (1u), 12C के एक परमाणु के द्रव्यमान के 1/12वें भाग के बराबर होती है|
1u = 1.660563 × 10–27 kg
3. नाभिक में एक निरावेशित कण होता है जिसे न्यूट्रॉन कहते हैं| इसका द्रव्यमान लगभग उतना ही होता है जितना प्रोटॉन का|
4. किसी तत्व की परमाणु संख्या Z उस तत्व के परमाण्विक नाभिक में प्रोटॉनों की संख्या होती है|
द्रव्यमान संख्या A, परमाण्विक नाभिक में प्रोटॉनों एवं न्यूट्रॉनों की कुल संख्या के बराबर होती है; A = Z + N; यहाँ Nनाभिक में विद्यमान न्यूट्रॉनों की संख्या निर्दिष्ट करता है|
एक नाभिकीय प्रजाति अथवा एक न्यूक्लाइड (nuclide) को 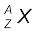 द्वारा व्यक्त करते हैं, जहाँ X उस रासायनिक प्रजाति का संकेत है|
द्वारा व्यक्त करते हैं, जहाँ X उस रासायनिक प्रजाति का संकेत है|
समान परमाणु संख्या Z, परंतु विभिन्न न्यूट्रॉन संख्या N के न्यूक्लाइड समस्थानिक कहलाते हैं| वे न्यूक्लाइड जिनके लिए द्रव्यमान संख्या A का मान समान हो सममारिक तथा वे जिनके लिए न्यूट्रॉन संख्या N का मान समान होसमन्युट्रॉनिक कहलाते हैं|
अधिकांश तत्व दो या अधिक समस्थानिकों के मिश्रण होते हैं| तत्व का परमाणु द्रव्यमान उसके समस्थानिकों के द्रव्यमानों का भारित माध्य होता है| जहाँ भार से तात्पर्य समस्थानिकों की सापेक्ष बहुलता से है|
5. नाभिक को गोलाकार मानकर उसकी एक त्रिज्या निर्धारित की जा सकती है| इलेक्ट्रॉन प्रकीर्णन प्रयोगों के आधार पर नाभिक की त्रिज्या ज्ञात की जा सकती है| यह पाया गया है कि नाभिकों की त्रिज्या निम्नलिखित सूत्र से व्यक्त होती है|
R = R0 A1/3,
जहाँ R0 = एक नियतांक = 1.2 fm. यह दर्शाता है कि नाभिक का घनत्व A पर निर्भर नहीं करता और यह 1017kg/m3 की कोटि का होता है|
6. नाभिक के अंदर न्यूट्रॉन एवं प्रोटॉन अल्प परासी प्रबल नाभिकीय बल द्वारा बँधे होते हैं| नाभिकीय बल न्यूट्रॉन एवं प्रोटॉन में विभेद नहीं करता|
7. नाभिकीय द्रव्यमान M हमेशा अपने अवयवों के कुल द्रव्यमान σm से कम होता है| नाभिक और इसके अवयवों के द्रव्यमानों का अंतर द्रव्यमान क्षति कहलाता है|
∆M = (Z mp + (A – Z)mn) – M
आइंसटाइन का द्रव्यमान-ऊर्जा सिद्धांत E = m c2 इस द्रव्यमान अंतर को ऊर्जा के रूप में इस प्रकार व्यक्त करता है :
∆Eb = ∆M c2
ऊर्जा ∆Eb नाभिक की बंधन-ऊर्जा कहलाती है| A = 30 से लेकर A = 170 द्रव्यमान संख्या के परास में प्रति न्यूक्लियॉन बंधन-ऊर्जा का मान लगभग नियत है| यह लगभग 8 MeV प्रति न्यूक्लियॉन है|
8. नाभिकीय प्रक्रियाओं से जुड़ी ऊर्जा रासायनिक प्रक्रियाओं की तुलना में लगभग दस लाख गुना अधिक होती है|
9. किसी नाभिकीय प्रक्रिया का Q-मान है ः
Q = अंतिम गतिज ऊर्जा – प्रारंभिक गतिज ऊर्जा
द्रव्यमान-ऊर्जा संरक्षण के कारण, कह सकते हैं कि
Q = (प्रारंभिक द्रव्यमानों का योग – अंतिम द्रव्यमानों का योग)c2
10. रेडियोएेक्टिवता वह परिघटना है जिसमें दी गई प्रजाति के नाभिक, α या β या γ किरणें उत्सर्जित करके रूपांतरित हो जाती हैं, जहाँ α-किरणें हीलियम के नाभिक हैं; β-किरणें इलैक्ट्रॉन हैं तथा γ-किरणें X-किरणों, से भी छोटी तरंगदैर्घ्य के विद्युत चुंबकीय विकिरण हैं|
11. रेडियोएेक्टिव क्षयता का नियम हैः N (t) = N(0) e–λt
यहाँ λ क्षयांक अथवा विघटन स्थिरांक है| किसी रेडियोनाभिक की अर्ध-आयु (T1/2) वह समय है जिसमें उनकी कुल संख्या N उनकी प्रारंभिक मान की आधी रह जाती है| औसत आयु τ वह समय है जिसने N अपने प्रारंभिक मान का e–1 गुण शेष रह जाता है|
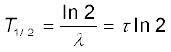
12. जब कम दृढ़ता से बंधित नाभिक अधिक दृढ़ता से बंधित नाभिक में परिवर्तित होता है तो ऊर्जा विमुक्त होती है| विखंडन में एक भारी नाभिक दो छोटे खंडों में विभाजित हो जाता है उदाहरणार्थ,
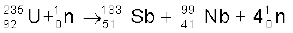
13. यह तथ्य कि विखंडन में जितने न्यूट्रॉन प्रयुक्त होते हैं उससे अधिक उत्पन्न होते हैं, शृंखला अभिक्रिया की संभावना प्रदान करता है| इस प्रक्रिया में उत्पन्न होने वाला प्रत्येक न्यूट्रॉन, नए विखंडन का प्रारंभ करता है| नाभिकीय बम विस्फोट में अनियंत्रित शृंखला अभिक्रिया तेजी से होती है| नाभिकीय रिएक्टर में यह नियंत्रित एवं स्थिर दर पर होती है| रिएक्टर में न्यूट्रॉन वृद्धि गुणांक k का मान 1 बनाये रखा जाता है|
14. संलयन में हलके नाभिक मिलकर एक बड़ा नाभिक बनाते हैं| सूर्य सहित सभी तारों में हाइड्रोजन नाभिकों का हीलियम नाभिकों में संलयन ऊर्जा का स्रोत है|
विचारणीय विषय
1. नाभिकीय द्रव्य का घनत्व नाभिक के साइज़ पर निर्भर नहीं करता है| परमाणु द्रव्यमान घनत्व इस नियम का पालन नहीं करता|
2. इलेक्ट्रॉन प्रकीर्णन द्वारा ज्ञात की गई नाभिक की त्रिज्या का मान एेल्फ़ा कण प्रकीर्णन के आधार पर ज्ञात की गई त्रिज्या से कुछ भिन्न पाया गया है| एेसा इसलिए है, क्योंकि, इलेक्ट्रॉन प्रकीर्णन नाभिक के आवेश वितरण से प्रभावित होता है जबकि एेल्फ़ा कण और उस जैसे अन्य कण नाभिकीय द्रव्य से प्रभावित होते हैं|
3. आइंस्टाइन द्वारा द्रव्यमान एवं ऊर्जा की समतुल्यता E = mc2 प्रदर्शित किए जाने के बाद अब हम द्रव्यमान संरक्षण एवं ऊर्जा संरक्षण के पृथक नियमों की बात नहीं करते, वरन द्रव्यमान-ऊर्जा संरक्षण के एक एकीकृत नियम की बात करते हैं| प्रकृति में यह नियम वस्तुतः प्रभावी है तथा इसका विश्वसनीय प्रमाण नाभिकीय भौतिकी में पाया जाता है| द्रव्यमान एवं ऊर्जा की समतुल्यता के नियम, नाभिकीय ऊर्जा एवं उसके शक्ति स्रोत के रूप में उपयोग का आधार है| इस नियम का उपयोग करके, किसी नाभिकीय प्रक्रिया (क्षय अथवा अभिक्रिया) के Q-मान को प्रारंभिक एवं अंतिम द्रव्यमानों के पदों में व्यक्त किया जा सकता है|
4. (प्रति न्यूक्लियॉन) बंधन-ऊर्जा वक्र की प्रकृति यह दर्शाती है कि ऊष्माक्षेपी नाभिकीय अभिक्रियाएँ संभव हैं जो दो हलके नाभिकों के संलयन से या एक भारी नाभिक के माध्यमिक द्रव्यमान वाले दो नाभिकों के विखंडन में देखी जा सकती हैं|
5. संलयन के लिए हलके नाभिकों में पर्याप्त प्रारंभिक ऊर्जा होनी चाहिए ताकि वे कूलॉम विभव अवरोध को पार कर सकें| यही कारण है कि संलयन के लिए अत्युच्च ताप की आवश्यकता होती है|
6. यद्यपि (प्रति न्यूक्लियॉन) बंधन-ऊर्जा वक्र संतत है और इसमें धीरे-धीरे ही परिवर्तन आता है परंतु इसमें 4He, 16O आदि न्यूक्लाइडों के लिए शिखर होते हैं| यह परमाणु की तरह ही नाभिक में भी शैल संरचना की विद्यमानता का प्रमाण माना जाता है|
7. ध्यान दें कि इलेक्ट्रॉन-पॉजिट्रॉन एक कण-प्रतिकण युग्म है| इनके द्रव्यमान एकसमान हैं| इनके आवेशों के परिमाण समान परंतु विपरीत प्रकृति के होते हैं| (यह पाया गया है कि जब एक इलेक्ट्रॉन एवं एक पॉजिट्रॉन एक साथ आते हैं तो एक-दूसरे का विलोपन (annihilation) कर देते हैं और γ-किरण फोटॉनों के रूप में ऊर्जा प्रदान करते हैं|
8. β--क्षय (इलेक्ट्रॉन उत्सर्जन) में इलेक्ट्रॉन के साथ उत्सर्जित होने वाला कण एंटी-न्यूट्रिनो (2315.png) है| इसके विपरीत β+-क्षय (पॉजिट्रॉन उत्सर्जन) में न्यूट्रिनो (ν) उत्सर्जित होता है| न्यूट्रिनो एवं एंटी-न्यूट्रिनो का युग्म कण-प्रतिकण युग्म होता है| प्रकृति में प्रत्येक कण का एक प्रतिकण होता है| तब एंटी-प्रोटॉन जो प्रोटॉन का प्रतिकण है, क्या होना चाहिए?
9. एक मुक्त न्यूट्रॉन अस्थायी होता है (2320.png)| परंतु, इसी तरह से मुक्त प्रोटॉन का क्षय संभव नहीं है| एेसा होने का कारण यह है कि प्रोटॉन का द्रव्यमान न्यूट्रॉन के द्रव्यमान की तुलना में थोड़ा कम होता है|
10. प्रायः एेल्फ़ा या बीटा उत्सर्जन के बाद गामा उत्सर्जन होता है| गामा फोटॉन उत्सर्जित करके कोई नाभिक उद्दीपित (उच्चतर) अवस्था से निम्नतर अवस्था में लौटता है| एेल्फ़ा अथवा बीटा उत्सर्जन के पश्चात कोई नाभिक उद्दीपित अवस्था में रह सकता है| एक ही नाभिक से (जैसे कि चित्र 13.4 में दर्शाये गए 60Ni के प्रकरण में) गामा किरणों का क्रमवार उत्सर्जन इस बात का स्पष्ट प्रमाण है कि नाभिकों में भी परमाणुओं की ही तरह विविक्त ऊर्जा स्तर होते हैं|
11. रेडियोएेक्टिवता नाभिक के अस्थायित्व का संसूचन है| हलके नाभिकों में स्थायित्व के लिए न्यूट्रॉनो एवं प्रोट्रॉनों की संख्या का अनुपात लगभग 1:1 होना चाहिए| भारी नाभिकों के स्थायित्व के लिए यह अनुपात 3:2 होना चाहिए| (प्रोटॉनों के मध्य लगने वाले प्रतिकर्षण के प्रभाव के निरसन के लिए अधिक न्यूट्रॉनों की आवश्यकता होगी|) इन स्थायित्व अनुपातों को न रखने वाले नाभिक अस्थायी होते हैं| इन नाभिकों में न्यूट्रॉनों अथवा प्रोटॉनों की अधिकता होती है| वास्तव में, (सभी तत्वों के) ज्ञात समस्थानिकों के मात्र लगभग 10% ही स्थायी हैं| अन्य नाभिक कृत्रिम रूप से प्रयोगशाला में बनाये जाते हैं (ये स्थायी नाभिकीय प्रजातियों पर α, p, d, n अथवा अन्य कणों के प्रघात द्वारा बनाये जाते हैं|)| अस्थायी समस्थानिक विश्व में पदार्थों के खगोलीय प्रेक्षणों में भी अवलोकित किए जाते हैं|
अभ्यास
अभ्यास के प्रश्न हल करने में निम्नलिखित आँकड़े आपके लिए उपयोगी सिद्ध होंगे :
e = 1.6×10–19C N = 6.023×1023 प्रति मोल
1/(4π∈0) = 9 × 109 N m2/C2 k = 1.381×10–23J K–1
1 MeV = 1.6×10–13J 1 u = 931.5 MeV/c2
1 year = 3.154×107 s
mH = 1.007825 u mn = 1.008665 u
m( ) = 4.002603 u me = 0.000548 u
) = 4.002603 u me = 0.000548 u
13.1 (a) लीथियम के दो स्थायी समस्थानिकों 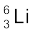 एवं
एवं 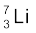 की बहुलता का प्रतिशत क्रमशः 7.5 एवं 92.5 हैं| इन समस्थानिकों के द्रव्यमान क्रमशः 6.01512 u एवं 7.01600 u हैं| लीथियम का परमाणु द्रव्यमान ज्ञात कीजिए|
की बहुलता का प्रतिशत क्रमशः 7.5 एवं 92.5 हैं| इन समस्थानिकों के द्रव्यमान क्रमशः 6.01512 u एवं 7.01600 u हैं| लीथियम का परमाणु द्रव्यमान ज्ञात कीजिए|
(b) बोरॉन के दो स्थायी समस्थानिक 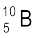 एवं
एवं 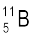 है| उनके द्रव्यमान क्रमशः 10.01294 u एवं 11.00931 u एवं बोरॉन का परमाणु भार 10.811 u है|
है| उनके द्रव्यमान क्रमशः 10.01294 u एवं 11.00931 u एवं बोरॉन का परमाणु भार 10.811 u है| 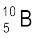 एवं
एवं 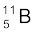 की बहुलता ज्ञात कीजिए|
की बहुलता ज्ञात कीजिए|
13.2 नियॉन के तीन स्थायी समस्थानिकों की बहुलता क्रमशः 90.51%, 0.27% एवं 9.22% है| इन समस्थानिकों के परमाणु द्रव्यमान क्रमशः 19.99 u, 20.99 u एवं 21.99 u हैं| नियॉन का औसत परमाणु द्रव्यमान ज्ञात कीजिए|
13.3 नाइट्रोजन नाभिक (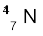 ) की बंधन-ऊर्जा MeV में ज्ञात कीजिए mN =14.00307 u
) की बंधन-ऊर्जा MeV में ज्ञात कीजिए mN =14.00307 u
13.4 निम्नलिखित आँकड़ों के आधार पर 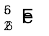 एवं
एवं 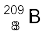 नाभिकों की बंधन-ऊर्जा MeV में ज्ञात कीजिए| m (
नाभिकों की बंधन-ऊर्जा MeV में ज्ञात कीजिए| m (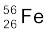 ) = 55.934939 u m (
) = 55.934939 u m (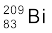 ) = 208.980388 u
) = 208.980388 u
13.5 एक दिए गए सिक्के का द्रव्यमान 3.0 g है| उस ऊर्जा की गणना कीजिए जो इस सिक्के के सभी न्यूट्रॉनों एवं प्रोटॉनों को एक-दूसरे से अलग करने के लिए आवश्यक हो| सरलता के लिए मान लीजिए कि सिक्का पूर्णतः 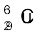 परमाणुओं का बना है (
परमाणुओं का बना है (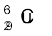 का द्रव्यमान = 62.92960 u)|
का द्रव्यमान = 62.92960 u)|
13.6 निम्नलिखित के लिए नाभिकीय समीकरण लिखिए ः
(i) 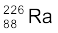 का α-क्षय (ii)
का α-क्षय (ii) 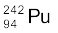 का α-क्षय
का α-क्षय
(iii) 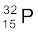 का β–-क्षय (iv)
का β–-क्षय (iv) 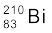 का β–-क्षय
का β–-क्षय
(v) 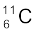 का β+-क्षय (vi)
का β+-क्षय (vi) 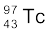 का β+-क्षय
का β+-क्षय
(vii) 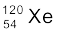 का इलेक्ट्रॉन अभिग्रहण
का इलेक्ट्रॉन अभिग्रहण
13.7 एक रेडियोएेक्टिव समस्थानिक की अर्धायु T वर्ष है| कितने समय के बाद इसकी एेक्टिवता, प्रारंभिक एेक्टिवता की (a) 3.125% तथा (b) 1% रह जाएगी|
13.8 जीवित कार्बनयुक्त द्रव्य की सामान्य एेक्टिवता, प्रति ग्राम कार्बन के लिए 15 क्षय प्रति मिनट है| यह एेक्टिवता, स्थायी समस्थानिक 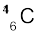 के साथ-साथ अल्प मात्रा में विद्यमान रेडियोएेक्टिव
के साथ-साथ अल्प मात्रा में विद्यमान रेडियोएेक्टिव 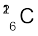 के कारण होती है| जीव की मृत्यु होने पर वायुमंडल के साथ इसकी अन्योन्य क्रिया (जो उपरोक्त संतुलित एेक्टिवता को बनाए रखती है) समाप्त हो जाती है, तथा इसकी एेक्टिवता कम होनी शुरू हो जाती है|
के कारण होती है| जीव की मृत्यु होने पर वायुमंडल के साथ इसकी अन्योन्य क्रिया (जो उपरोक्त संतुलित एेक्टिवता को बनाए रखती है) समाप्त हो जाती है, तथा इसकी एेक्टिवता कम होनी शुरू हो जाती है| 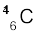 की ज्ञात अर्धायु (5730 वर्ष) और नमूने की मापी गई एेक्टिवता के आधार पर इसकी सन्निकट आयु की गणना की जा सकती है| यही पुरातत्व विज्ञान में प्रयुक्त होने वाली
की ज्ञात अर्धायु (5730 वर्ष) और नमूने की मापी गई एेक्टिवता के आधार पर इसकी सन्निकट आयु की गणना की जा सकती है| यही पुरातत्व विज्ञान में प्रयुक्त होने वाली 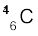 कालनिर्धारण (dating) पद्धति का सिद्धांत है| यह मानकर कि मोहनजोदड़ो से प्राप्त किसी नमूने की एेक्टिवता 9 क्षय प्रति मिनट प्रति ग्राम कार्बन है| सिंधु घाटी सभ्यता की सन्निकट आयु का आकलन कीजिए|
कालनिर्धारण (dating) पद्धति का सिद्धांत है| यह मानकर कि मोहनजोदड़ो से प्राप्त किसी नमूने की एेक्टिवता 9 क्षय प्रति मिनट प्रति ग्राम कार्बन है| सिंधु घाटी सभ्यता की सन्निकट आयु का आकलन कीजिए|
13.9 8.0 mCi सक्रियता का रेडियोएेक्टिव स्रोत प्राप्त करने के लिए 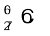 की कितनी मात्रा की आवश्यकता होगी?
की कितनी मात्रा की आवश्यकता होगी? 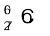 की अर्धायु 5.3 वर्ष है|
की अर्धायु 5.3 वर्ष है|
13.10 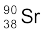 की अर्धायु 28 वर्ष है| इस समस्थानिक के 15 mg की विघटन दर क्या है?
की अर्धायु 28 वर्ष है| इस समस्थानिक के 15 mg की विघटन दर क्या है?
13.11 स्वर्ण के समस्थानिक 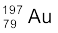 एवं रजत के समस्थानिक
एवं रजत के समस्थानिक 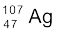 की नाभिकीय त्रिज्या के अनुपात का सन्निकट मान ज्ञात कीजिए|
की नाभिकीय त्रिज्या के अनुपात का सन्निकट मान ज्ञात कीजिए|
13.12 (a) 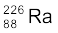 एवं (b)
एवं (b) 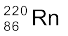 नाभिकों के α-क्षय में उत्सर्जित α-कणों का Q-मान एवं गतिज ऊर्जा ज्ञात कीजिए|
नाभिकों के α-क्षय में उत्सर्जित α-कणों का Q-मान एवं गतिज ऊर्जा ज्ञात कीजिए|
दिया हैः m (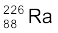 ) = 226.02540 u, m (
) = 226.02540 u, m (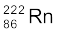 ) = 222.01750 u,
) = 222.01750 u,
m (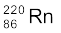 ) = 220.01137 u, m (
) = 220.01137 u, m (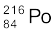 ) = 216.00189 u.
) = 216.00189 u.
13.13 रेडियोन्यूक्लाइड 11C का क्षय निम्नलिखित समीकरण के अनुसार होता है,
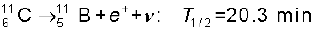
उत्सर्जित पॉजिट्रॉन की अधिकतम ऊर्जा 0.960 MeV है| द्रव्यमानों के निम्नलिखित मान दिए गए हैं
m (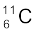 ) = 11.011434 u तथा m (
) = 11.011434 u तथा m ( ) = 11.009305 u,
) = 11.009305 u,
Q-मान की गणना कीजिए एवं उत्सर्जित पॉजिट्रॉन की अधिकतम ऊर्जा के मान से इसकी तुलना कीजिए|
13.14 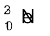 का नाभिक, β– उत्सर्जन के साथ क्षयित होता है| इस β-क्षय के लिए समीकरण लिखिए और उत्सर्जित इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा ज्ञात कीजिए| m (
का नाभिक, β– उत्सर्जन के साथ क्षयित होता है| इस β-क्षय के लिए समीकरण लिखिए और उत्सर्जित इलेक्ट्रॉनों की अधिकतम गतिज ऊर्जा ज्ञात कीजिए| m ( ) = 22.994466 u u; m (
) = 22.994466 u u; m ( ) = 22.989770 u,
) = 22.989770 u,
13.15 किसी नाभिकीय अभिक्रिया A + b → C + d का Q-मान निम्नलिखित समीकरण द्वारा परिभाषित होता है,
Q = [ mA + mb – mC – md]c2
जहाँ दिए गए द्रव्यमान, नाभिकीय विराम द्रव्यमान (rest mass) हैं| दिए गए आँकड़ों के आधार पर बताइए कि निम्नलिखित अभिक्रियाएँ ऊष्माक्षेपी हैं या ऊष्माशोषी|
(i) 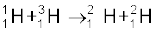
(ii) 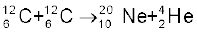
दिए गए परमाणु द्रव्यमान इस प्रकार हैं ः
m (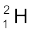 ) = 2.014102 u
) = 2.014102 u
m (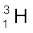 ) = 3.016049 u
) = 3.016049 u
m (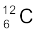 ) = 12.000000 u
) = 12.000000 u
m ( ) = 19.992439 u
) = 19.992439 u
13.16 माना कि हम 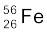 नाभिक के दो समान अवयवों
नाभिक के दो समान अवयवों 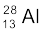 में विखंडन पर विचार करें| क्या ऊर्जा की दृष्टि से यह विखंडन संभव है? इस प्रक्रम का Q-मान ज्ञात करके अपना तर्क प्रस्तुत करें|
में विखंडन पर विचार करें| क्या ऊर्जा की दृष्टि से यह विखंडन संभव है? इस प्रक्रम का Q-मान ज्ञात करके अपना तर्क प्रस्तुत करें|
दिया है ः m (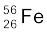 ) = 55.93494 u एवं m (
) = 55.93494 u एवं m (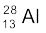 ) = 27.98191 u
) = 27.98191 u
13.17 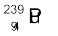 के विखंडन गुण बहुत कुछ
के विखंडन गुण बहुत कुछ 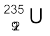 से मिलते-जुलते हैं| प्रति विखंडन विमुक्त औसत ऊर्जा 180 MeV है| यदि 1 kg शुद्ध
से मिलते-जुलते हैं| प्रति विखंडन विमुक्त औसत ऊर्जा 180 MeV है| यदि 1 kg शुद्ध 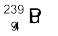 के सभी परमाणु विखंडित हों तो कितनी MeV ऊर्जा विमुक्त होगी?
के सभी परमाणु विखंडित हों तो कितनी MeV ऊर्जा विमुक्त होगी?
13.18 किसी1000 MW विखंडन रिएक्टर के आधे ईंधन का 5.00 वर्ष में व्यय हो जाता है| प्रारंभ में इसमें कितना 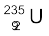 था? मान लीजिए कि रिएक्टर 80% समय कार्यरत रहता है, इसकी संपूर्ण ऊर्जा
था? मान लीजिए कि रिएक्टर 80% समय कार्यरत रहता है, इसकी संपूर्ण ऊर्जा 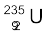 के विखंडन से ही उत्पन्न हुई है; तथा
के विखंडन से ही उत्पन्न हुई है; तथा 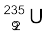 न्यूक्लाइड केवल विखंडन प्रक्रिया में ही व्यय होता है|
न्यूक्लाइड केवल विखंडन प्रक्रिया में ही व्यय होता है|
13.19 2.0 kg ड्यूटीरियम के संलयन से एक 100 वाट का विद्युत लैंप कितनी देर प्रकाशित रखा जा सकता है? संलयन अभिक्रिया निम्नवत ली जा सकती है
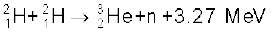
13.20 दो ड्यूट्रॉनों के आमने-सामने की टक्कर के लिए कूलॉम अवरोध की ऊँचाई ज्ञात कीजिए| (संकेत-कूलॉम अवरोध की ऊँचाई का मान इन ड्यूट्रॉन के बीच लगने वाले उस कूलॉम प्रतिकर्षण बल के बराबर होता है जो एक-दूसरे को संपर्क में रखे जाने पर उनके बीच आरोपित होता है| यह मान सकते हैं कि ड्यूट्रॉन 2.0 fm प्रभावी त्रिज्या वाले दृढ़ गोले हैं|)
13.21 समीकरण R = R0A1/3 के आधार पर, दर्शाइए कि नाभिकीय द्रव्य का घनत्व लगभग अचर है (अर्थात A पर निर्भर नहीं करता है)| यहाँ R0 एक नियतांक है एवं A नाभिक की द्रव्यमान संख्या है|
13.22 किसी नाभिक से β+ (पॉजिट्रॉन) उत्सर्जन की एक अन्य प्रतियोगी प्रक्रिया है जिसे इलेक्ट्रॉन परिग्रहण (Capture) कहते हैं (इसमें परमाणु की आंतरिक कक्षा, जैसे कि K-कक्षा, से नाभिक एक इलेक्ट्रॉन परिगृहीत कर लेता है और एक न्यूट्रिनो, v उत्सर्जित करता है)|
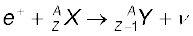
दर्शाइए कि यदि β+ उत्सर्जन ऊर्जा विचार से अनुमत है तो इलेक्ट्रॉन परिग्रहण भी आवश्यक रूप से अनुमत है, परंतु इसका विलोम अनुमत नहीं है|
अतिरिक्त अभ्यास
13.23 आवर्त सारणी में मैग्नीशियम का औसत परमाणु द्रव्यमान 24.312 u दिया गया है| यह औसत मान, पृथ्वी पर इसके समस्थानिकों की सापेक्ष बहुलता के आधार पर दिया गया है| मैग्नीशियम के तीनों समस्थानिक तथा उनके द्रव्यमान इस प्रकार हैं – 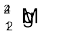 (23.98504 u),
(23.98504 u), 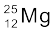 (24.98584) एवं
(24.98584) एवं 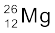 (25.98259 u)| प्रकृति में प्राप्त मैग्नीशियम में
(25.98259 u)| प्रकृति में प्राप्त मैग्नीशियम में 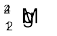 की (द्रव्यमान के अनुसार) बहुलता 78.99% है| अन्य दोनों समस्थानिकों की बहुलता का परिकलन कीजिए|
की (द्रव्यमान के अनुसार) बहुलता 78.99% है| अन्य दोनों समस्थानिकों की बहुलता का परिकलन कीजिए|
13.24 न्यूट्रॉन पृथक्करण ऊर्जा (Separation energy), परिभाषा के अनुसार, वह ऊर्जा है जो किसी नाभिक से एक न्यूट्रॉन को निकालने के लिए आवश्यक होती है| नीचे दिए गए आँकड़ों का इस्तेमाल करके 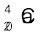 एवं
एवं 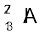 नाभिकों की न्यूट्रॉन पृथक्करण ऊर्जा ज्ञात कीजिए|
नाभिकों की न्यूट्रॉन पृथक्करण ऊर्जा ज्ञात कीजिए|
m(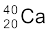 ) = 39.962591 u
) = 39.962591 u
m(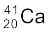 ) = 40.962278 u
) = 40.962278 u
m(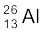 ) = 25.986895 u
) = 25.986895 u
m(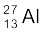 ) = 26.981541 u
) = 26.981541 u
13.25 किसी स्रोत में फॉस्फोरस के दो रेडियो न्यूक्लाइड निहित हैं 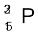 (T1/2 = 14.3 d) एवं
(T1/2 = 14.3 d) एवं 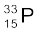
(T1/2 = 25.3 d)| प्रारंभ में 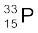 से 10% क्षय प्राप्त होता है| इससे 90% क्षय प्राप्त करने के लिए कितने समय प्रतीक्षा करनी होगी?
से 10% क्षय प्राप्त होता है| इससे 90% क्षय प्राप्त करने के लिए कितने समय प्रतीक्षा करनी होगी?
13.26 कुछ विशिष्ट परिस्थितियों में, एक नाभिक, α-कण से अधिक द्रव्यमान वाला एक कण उत्सर्जित करके क्षयित होता है| निम्नलिखित क्षय-प्रक्रियाओं पर विचार कीजिए ः
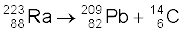
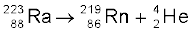
इन दोनों क्षय प्रक्रियाओं के लिए Q-मान की गणना कीजिए और दर्शाइए कि दोनों प्रक्रियाएँ ऊर्जा की दृष्टि से संभव हैं|
13.27 तीव्र न्यूट्रॉनों द्वारा 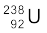 के विखंडन पर विचार कीजिए| किसी विखंडन प्रक्रिया में प्राथमिक अंशों (Primaryfragments) के बीटा-क्षय के पश्चात कोई न्यूट्रॉन उत्सर्जित नहीं होता तथा
के विखंडन पर विचार कीजिए| किसी विखंडन प्रक्रिया में प्राथमिक अंशों (Primaryfragments) के बीटा-क्षय के पश्चात कोई न्यूट्रॉन उत्सर्जित नहीं होता तथा 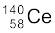 तथा
तथा  अंतिम उत्पाद प्राप्त होते हैं| विखंडन प्रक्रिया के लिए Q के मान का परिकलन कीजिए| आवश्यक आँकड़े इस प्रकार हैं ः
अंतिम उत्पाद प्राप्त होते हैं| विखंडन प्रक्रिया के लिए Q के मान का परिकलन कीजिए| आवश्यक आँकड़े इस प्रकार हैं ः
m(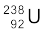 ) =238.05079 u
) =238.05079 u
m(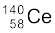 ) =139.90543 u
) =139.90543 u
m( ) = 98.90594 u
) = 98.90594 u
13.28 D-T अभिक्रिया (ड्यूटीरियम-ट्रीटियम संलयन), 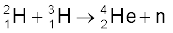 पर विचार कीजिए|
पर विचार कीजिए|
(a) नीचे दिए गए आँकड़ों के आधार पर अभिक्रिया में विमुक्त ऊर्जा का मान MeV में ज्ञात कीजिए|
m(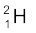 ) =2.014102 u
) =2.014102 u
m(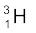 ) =3.016049 u
) =3.016049 u
(b) ड्यूटीरियम एवं ट्राइटियम दोनों की त्रिज्या लगभग 1.5 fm मान लीजिए| इस अभिक्रिया में, दोनों नाभिकों के मध्य कूलॉम प्रतिकर्षण से पार पाने के लिए कितनी गतिज ऊर्जा की आवश्यकता है? अभिक्रिया प्रारंभ करने के लिए गैसों(D तथा T गैसें) को किस ताप तक ऊष्मित किया जाना चाहिए?
(संकेत ः किसी संलयन क्रिया के लिए आवश्यक गतिज ऊर्जा = संलयन क्रिया में संलग्न कणों की औसत तापीय गतिज ऊर्जा = 2 (3kT/2); k ः बोल्ट्ज़मान नियतांक तथा
T = परम ताप)
13.29 नीचे दी गई क्षय-योजना में, γ-क्षयों की विकिरण आवृत्तियाँ एवं β-कणों की अधिकतम गतिज ऊर्जाएँ ज्ञात कीजिए| दिया है :
m(198Au) = 197.968233 u
m(198Hg) =197.966760 u
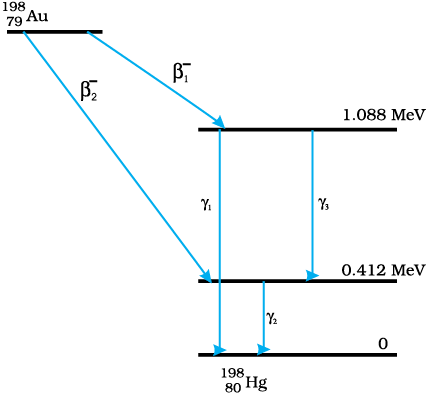
चित्र 13.6
13.30 सूर्य के अभ्यंतर में (a) 1 kg हाइड्रोजन के संलयन के समय विमुक्त ऊर्जा का परिकलन कीजिए| (b) विखंडन रिएक्टर में 1.0 kg 235U के विखंडन में विमुक्त ऊर्जा का परिकलन कीजिए| (c) तथा (b) प्रश्नों में विमुक्त ऊर्जाओं की तुलना कीजिए|
13.31 मान लीजिए कि भारत का लक्ष्य 2020 तक 200,000 MW विद्युत शक्ति जनन का है| इसका 10% नाभिकीय शक्ति संयंत्रों से प्राप्त होना है| माना कि रिएक्टर की औसत उपयोग दक्षता (ऊष्मा को विद्युत में परिवर्तित करने की क्षमता) 25% है| 2020 के अंत तक हमारे देश को प्रति वर्ष कितने विखंडनीय यूरेनियम की आवश्यकता होगी| 235U प्रति विखंडन उत्सर्जित ऊर्जा 200 MeV है|