For the matrix 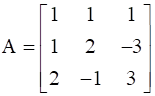
Show that A3– 6A2 + 5A + 11 I = O. Hence, find A–1.
Here A2 = A.A =
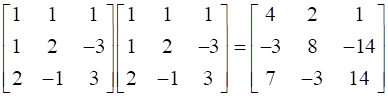
And hence A3 = A. A2 =
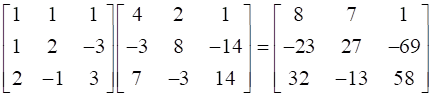
∴ A3– 6A2 + 5A + 11 I =
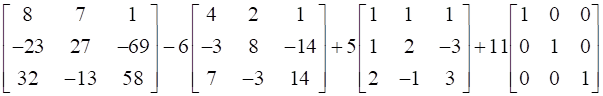
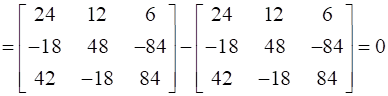
Thus, A3– 6A2 + 5A + 11 I = 0
Now, A3– 6A2 + 5A + 11 I = 0,
→ (A.A.A)- 6 (A.A) +5A = -11I
Post-multiply with A-1 on both sides-
→ (A.A.A.A-1)- 6 (A.A.A-1) +5A.A-1 = -11I. A-1
→ (A.A.I) – 6(A.I) + 5I = -11I. A-1 {since A.A-1 = I}
→ (A.A) – 6A +5I = -11A-1 {since X.I = X}
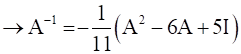
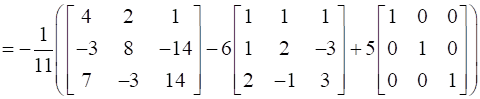
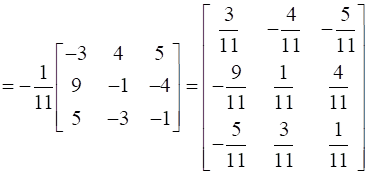
Hence 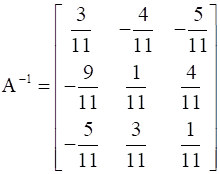
18