Fill in the blanks
The result tan–1 x – tan–1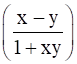 is true when value of xy is _________.
is true when value of xy is _________.
The result tan–1 x – tan–1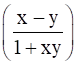 is true when value of xy is > -1.
is true when value of xy is > -1.
We have,
![]()
Principal range of tan-1a is ![]()
Let tan-1x = A and tan-1y = B … (1)
So, A,B ϵ ![]()
We know that, ![]() … (2)
… (2)
From (1) and (2), we get,
![]()
Applying, tan-1 both sides, we get,
![]()
As, principal range of tan-1a is ![]() .
.
So, for tan-1tan(A-B) to be equal to A-B,
A-B must lie in ![]() – (3)
– (3)
Now, if both A,B < 0, then A, B ϵ ![]()
∴ A ϵ ![]() and -B ϵ
and -B ϵ ![]()
So, A – B ϵ ![]()
So, from (3),
tan-1tan(A-B) = A-B
![]()
Now, if both A,B > 0, then A, B ϵ ![]()
∴ A ϵ ![]() and -B ϵ
and -B ϵ ![]()
So, A – B ϵ ![]()
So, from (3),
tan-1tan(A-B) = A-B
![]()
Now, if A > 0 and B < 0,
Then, A ϵ ![]() and B ϵ
and B ϵ ![]()
∴ A ϵ ![]() and -B ϵ
and -B ϵ ![]()
So, A – B ϵ (0,π)
But, required condition is A – B ϵ ![]()
As, here A – B ϵ (0,π), so we must have A – B ϵ ![]()
![]()
![]()
Applying tan on both sides,
![]()
As, ![]()
So, tan A < - cot B
Again, ![]()
So, ![]()
⇒ tan A tan B < -1
As, tan B < 0
xy > -1
Now, if A < 0 and B > 0,
Then, A ϵ ![]() and B ϵ
and B ϵ ![]()
∴ A ϵ ![]() and -B ϵ
and -B ϵ ![]()
So, A – B ϵ (-π,0)
But, required condition is A – B ϵ ![]()
As, here A – B ϵ (0,π), so we must have A – B ϵ ![]()
![]()
![]()
Applying tan on both sides,
![]()
As, ![]()
So, tan B > - cot A
Again, ![]()
So, ![]()
⇒ tan A tan B > -1
⇒xy > -1