Using the properties of determinants in evaluate:
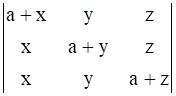
Let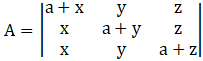
Expanding |A| along C1, we get
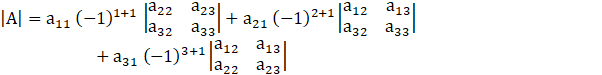
![]()
= (a + x) [(a + y)(a + z) – yz] – y [(x)(a + z) – xz] + z [xy – x (a + y)]
= (a + x) [a2 + az + ya + yz – yz] – y [ax + xz – xz] + z [xy – xa + xy]
= (a + x) [a2 + az + ya] – y [ax] + z [– xa]
= a(a2 + az + ya) + x(a2 + az + ya) – yax – zxa
= a3 + a2z + ya2 + xa2 + xaz + xya – yax – zxa
= a3 + a2z + ya2 + xa2
= a2 (a + z + y + x)
3