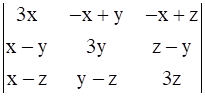
Let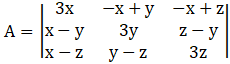

By applying C₁→ C₁ + C₂ + C₃, we have

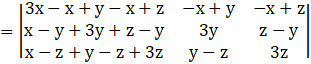
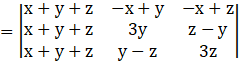
Taking (x + y + z) common from Column C₁, we get

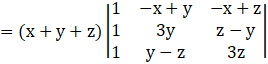
By applying R₂→ R₂ – R₁, we get

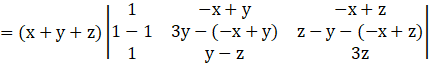
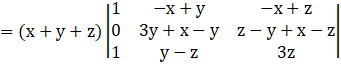
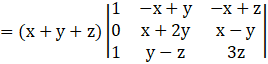
By applying R₃→ R₃ – R₁, we get

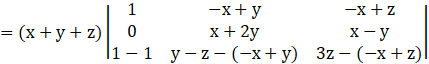
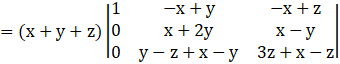
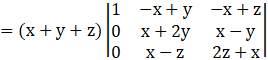
Applying C₂→ C₂ – C₃, we get

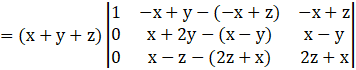
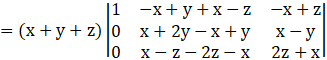
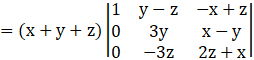
Now, expanding along C₁, we get

= (x + y + z) [1×{(3y)(2z + x) – (-3z)(x – y)}]

= (x + y + z) [6yz + 3yx + (3z)(x – y)]

= (x + y + z) [6yz + 3yx + 3zx – 3zy]

= (x + y + z) [3yz + 3zx + 3yx]

= 3(x + y + z)(yz + zx + yx)