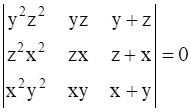
Taking LHS,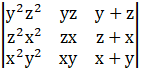

Firstly, multiply and divide R₁, R₂, R₃ by x, y, z respectively, we get

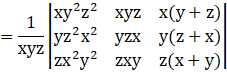
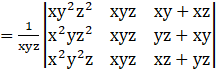[rearrange the terms]

Taking xyz common from the first and second column, we get

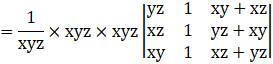
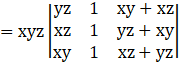
Applying C₃→ C₃ + C₁, we get

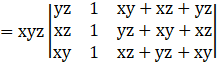
Taking common (xy + yz + xz) common from C₃, we get

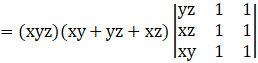
If any two columns (or rows) of a determinant are identical (all corresponding elements are same), then the value of determinant is zero.

Here, C₂ and C₃ are identical.

Hence,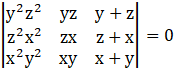

∴ LHS = RHS

Hence Proved