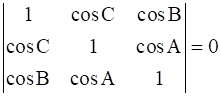
Given: A + B + C = 0

To Prove: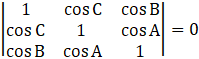

Taking LHS,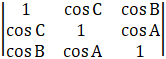

Expanding along the first row, we get

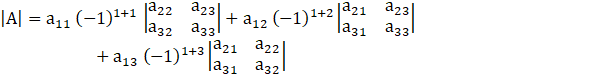
= [1{1 – cos²A} – cos C {cos C – cos B cos A} + cos B {cos C cos A – cos B}]

= {1 – cos²A} – {cos²C – cos A cos B cos C} + {cos A cos B cos C – cos²B}

= {sin²A} – cos²C + cos A cos B cos C + cos A cos B cos C – cos²B

[∵ cos²x + sin²x = 1]

= sin²A – cos²C – cos²B + 2cos A cos B cos C

= -(cos²B – sin²A)– cos²C + 2cos A cos B cos C

= -[cos(B + A)cos(B – A)] + cos C [2 cos A cos B – cos C]

[∵ cos²B – sin²A = cos(B + A)cos(B – A)]

= -[cos(B + A)cos(B – A)] + cos C [cos(A + B) + cos(A – B) – cos C]…(i)

[∵ 2cos A cos B = cos(A + B) + cos(A – B)]

It is given that A + B + C = 0

⇒ A + B = - C

Putting the value of A + B in eq (i), we get

= -[cos(- C) cos(B – A)] + cos C [cos(-C) + cos (A – B) – cos C]

= -cos C cos(B – A) + cos C[cos C + cos(A – B) – cos C]

[∵ cos(-C) = cos C]

Now, cos(A – B) = cos A cos B + sin A sin B

= -cos C{cos B cos A + sin B sin A} + cos C [cos A cos B + sin A sin B]

= 0 = RHS

Hence Proved