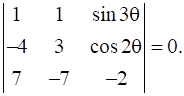
We have,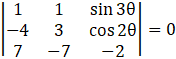

Expanding along R₁, we get

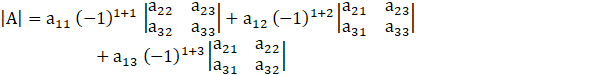
⇒ (1){-6 – {(-7) cos2θ}} – 1{8 – 7cos2θ} + sin3θ {28 – 21} = 0

⇒ – 6 + 7cos2θ – 8 + 7cos2θ + 7sin3θ = 0

⇒ 14cos2θ + 7sin3θ – 14 = 0

⇒ 2cos2θ + sin3θ – 2 = 0

Now, we know that

cos 2θ = 1 – 2sin²θ

sin 3θ = 3sinθ – 4sin³θ

⇒ 2(1 – 2sin²θ) + (3sinθ – 4sin³θ) – 2 = 0

⇒ 2 – 4sin²θ + 3sinθ – 4sin³θ – 2 = 0

⇒ -2 + 4sin²θ - 3sinθ + 4sin³θ + 2 = 0

⇒ sinθ (4sinθ – 3 + 4sin²θ) = 0

⇒ sinθ (4sin²θ – 6sinθ + 2sinθ – 3) = 0

⇒ sinθ [2sinθ(2sinθ – 3) + 1(2sinθ – 3)] = 0

⇒ sinθ (2sinθ + 1)(2sinθ – 3) = 0

⇒ sinθ = 0 or 2sinθ + 1 = 0 or 2sinθ – 3 = 0

⇒ θ = nπ or 2sinθ = -1 or 2sinθ = 3

⇒

⇒ θ = nπ ; m, n ∈ Z