If 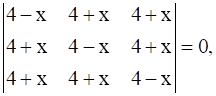 then find values of x.
then find values of x.
We have, 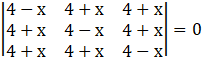
By applying C1→ C1 + C2 + C3, we get
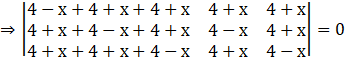
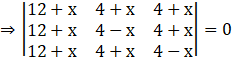
Taking (12 + x) common from the first column, we get
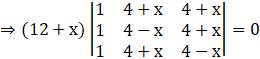
By applying C2→ C2 + C3, we get
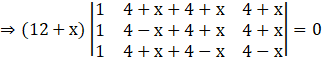
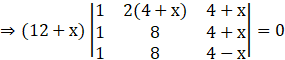
Applying R2→ R2 – R3, we get
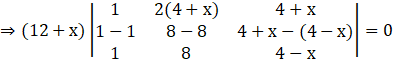
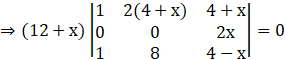
Applying R3→ R3 – R1, we get
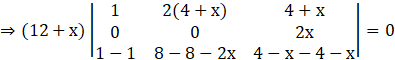
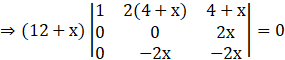
Expanding along first column, we get
⇒ (12 + x)[(1){0 – (2x)(-2x)}] = 0
⇒ (12 + x)(4x2) = 0
⇒ 12 + x = 0 or 4x2 = 0
⇒ x = -12 or x = 0
Hence, the value of x = -12 and 0
13