If a1, a2, a3, ..., ar are in G.P., then prove that the determinant 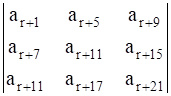 is independent of r.
is independent of r.
Given: a1, a2…, ar are in G.P
We know that, ar+1 = AR(r+1)-1 = ARr …(i)
[∵an = arn-1, where a = first term and r = common ratio]
where A = First term of given G.P
and R = common ratio of G.P
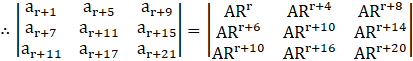 …[from(i)]
…[from(i)]
Taking ARr, ARr+6 and ARr+10 common from R1, R2 and R3 respectively, we get
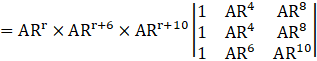
If any two columns (or rows) of a determinant are identical (all corresponding elements are same), then the value of determinant is zero.
Here, R1 and R2 are identical.
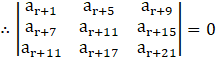
Hence Proved
14