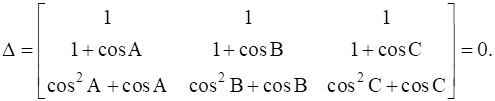
We have,

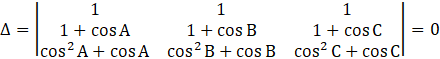
Applying C₂→ C₂ – C₁, we get

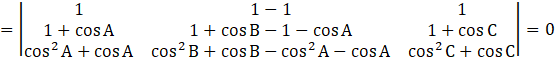
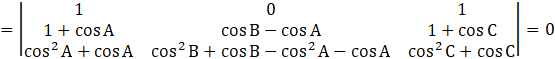
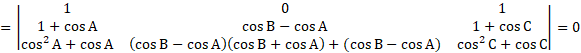
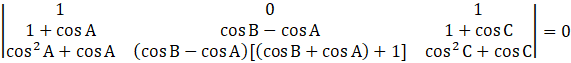
Taking common cos B – cos A from second column, we get

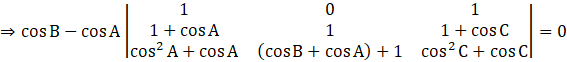
Applying C₃→ C₃ – C₁, we get

⇒

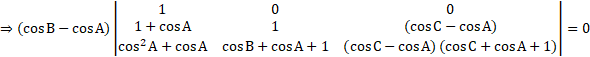
Taking common cos C – cos A from column third, we get

Now, expanding along first row, we get

⇒ (cos B – cos A)(cos C – cos A)[(1){cos C + cos A + 1 – (cos B + cos A + 1)}] = 0

⇒ (cos B – cos A)(cos C – cos A)[cos C + cos A + 1 – cos B – cos A – 1] = 0

⇒ (cos B – cos A)(cos C – cos A)(cos C – cos B) = 0

⇒ cos B – cos A = 0 or cos C – cos A = 0 or cos C – cos B = 0

⇒ cos B = cos A or cos C = cos A or cos C = cos B

⇒ B = A or C = A or C = B

Hence, ΔABC is an isosceles triangle.