If a + b + c ≠ 0 and 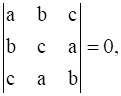 then prove that a = b = c.
then prove that a = b = c.
Let 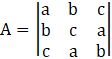
Applying C1→ C1 + C2 + C3, we get
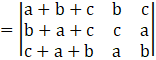
Taking (a + b + c) common from the first column, we get
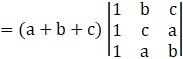
Now, Expanding along C1, we get
= (a + b + c)[(1)(bc – a2) – (1)(b2 – ac) + (1)(ba – c2)]
= (a + b + c)[bc – a2 – b2 + ac + ab – c2]
= (a + b + c)[-(a2 + b2 + c2 – ab – bc – ac)]
![]()
![]()
![]()
[∵ (a – b)2 = a2 + b2 – 2ab]
Given that Δ = 0
![]()
⇒ (a + b + c)[(a – b)2 + (b – c)2 + (c – a)2] = 0
Either (a + b + c) = 0 or (a – b)2 + (b – c)2 + (c – a)2 = 0
but it is given that (a + b + c) ≠ 0
∴(a – b)2 + (b – c)2 + (c – a)2 = 0
⇒ a – b = b – c = c – a = 0
⇒ a = b = c
Hence Proved
21