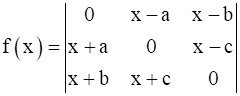Given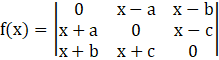

Option (A):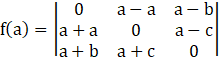

= 0 – 0 + (a – b) [2a (a + c) – 0 (a + b)]

= (a – b) [2a² + 2ac – 0]

= (a – b) (2a² + 2ac) ≠ 0

Option (B):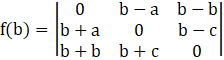

= 0 – (b - a) [(b + a) (0) – (b – c) (2b)] + 0

= - (b – a) [0 - 2b² + 2bc]

= (a – b) (2b² – 2bc) ≠ 0

Option (C):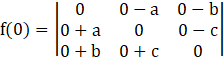

= 0 + a [a (0) – (-bc)] – b [ac – b (0)]

= a [bc] – b [ac]

= abc – abc = 0

Option (D):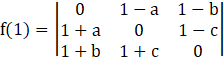

= 0 – (1 - a) [(1 + a) (0) – (1 – c) (1 + b)] + (1 – b) [ (1 + a) (1 + c) – 0 (1 + b)]

= - (1 – a) [- (1 – c) (1 + b)] + (1 – b) [(1 + a) (1 + c)]

= (1 – a) (1 – c) (1 + b) + (1 – b) (1 + a) (1 + c) ≠ 0

Hence, option (C) satisfies.