The value of the determinant 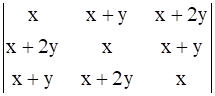 is
is
Given matrix 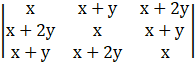
![]()
= x [x2 – (x + y) (x + 2y)] – (x + y) [(x + 2y) (x) – (x + y)2] + (x + 2y) [(x + 2y)2 – x (x + y)]
= x [x2 – x2 – 3xy – 2y2] – (x + y) [x2 + 2xy – x2 – 2xy – y2] + (x + 2y) [x2 + 4xy + 4y2 – x2 – xy]
= x [-3xy – 2y2] – (x + y) [-y2] + (x + 2y) [3xy + 4y2]
= -3x2y – 2xy2 + xy2 + y3 +3x2y + 4xy2 + 6xy2 + 8y3
= 9y3 + 9xy2
= 9y2 (x + y) … option (B)
Hence, option B satisfies.
36