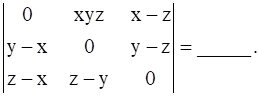
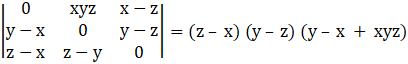
Explanation:

Given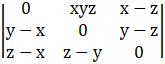

Performing the operation C₁→ C₁ – C₃

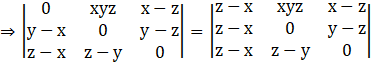
Taking (z – x) common from C₁,

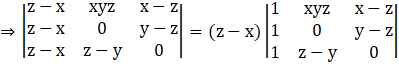
= (z – x) [1 [0 – (y – z) (z – y)] - (xyz) [0 - (y - z)] + (x – z) [(z – y) – 0]]

= (z – x) (z – y) (-y + z – xyz + x – z)

= (z – x) (z – y) (x – y – xyz)

= (z – x) (y – z) (y – x + xyz)