Given: two men A and B start with velocities v at the same time from the junction of the two roads inclined at 45° to each other

To find the rate at which they are being separated

Explanation:

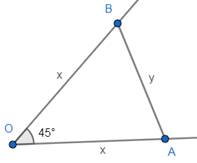
Let A and B move a distance of x on different roads as shown above, there distance at any time t will be same as they have same velocity.

Hence

Now consider ΔAOB, applying the cosine rule, we get

y² = x²+x²-2x.x.cos 45°

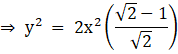
Now multiplying and dividing by √2, we get

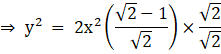
Now applying the derivative with respect to t, we get

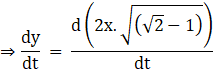
Taking out the constant terms, we get

Substituting the value from equation (i), we get

Hence this is the rate at which the two roads are being separated