A man, 2m tall, walks at the rate of 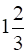 m/s towards a street light which is
m/s towards a street light which is 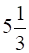 m above the ground. At what rate is the tip of his shadow moving? At what rate is the length of the shadow changing when he is
m above the ground. At what rate is the tip of his shadow moving? At what rate is the length of the shadow changing when he is 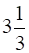 m from the base of the light?
m from the base of the light?
Given: a 2m tall man walks at the rate of ![]() m/s towards a
m/s towards a ![]() m tall street light.
m tall street light.
To find: the rate at which the tip of the shadow is moving and also to find the rate at which the length of the shadow changing when he is ![]() m from the base of the light.
m from the base of the light.
Explanation:

Here the street light is AB = ![]()
And man is DC = 2m
Let BC = x m and CE = y m
And given man walks towards the streetlight at a rate of ![]() , and it will negative because the man is moving towards the street light
, and it will negative because the man is moving towards the street light
Hence ![]() ………(i)
………(i)
Now consider ΔABE and ΔDCE
∠DEC = ∠AEB (same angle)
∠DCE = ∠ABD = 90°
Hence by AA similarity,
ΔABE≅ΔDCE
Hence by CPCT,
![]()
Now substituting the values from the figure, we get

![]()
⇒ 16y = 6(x+y)
⇒ 16y = 6x+6y
⇒ 16y-6y = 6x
⇒ 10y = 6x
![]()
![]()
Now applying first derivative with respect to t, we get

![]()
Now substituting the value from equation (i) in above equation, we get
![]()
![]()
![]()
Hence the rate at which the tip of the shadow is moving is -1m/s, i.e., the length of the shadow is decreasing at the rate of 1m/s.
Let BE = z
So from fig,
z = x+y
Applying the first derivative on above equation with respect to t, we get
![]()
Now substituting the corresponding values, we get
![]()
![]()
![]()
![]()
![]()
Hence the tip of the shadow is moving at the rate of ![]() towards the light source.
towards the light source.