Given: two squares of sides x and y, such that y = x-x²

To find: the rate of change of the area of the second square with respect to the area of the first square

Explanation: Let the area of the first and the second square be A₁ and A₂ respectively.

Then Area of the first square is

A₁ = x²

Differentiating this with respect to time, we get

And the area of the second square is

A₂ = y²…….(ii)

But given, y = x-x²

Substituting this given value in equation (ii), we get

A₂ = (x-x²)² …….(iii)

Now differentiating equation (iii) with respect to t, we get

Now applying the power rule of differentiation, we get

Now applying the sum rule of differentiation, we get

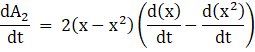
Applying the derivative, we get

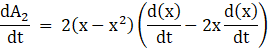
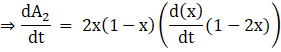
We need to find the rate of change of area of the second square with respect to the area of the first square, i.e.,

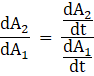
Substituting values from equation (i) and (iv), we get

By cancelling the like terms we get

Hence the rate of change of the area of the second square with respect to the area of the first square is 2x²-3x+1