Given: two curves 2x = y² and 2xy = k

To find: the condition that these two curves intersect orthogonally

Explanation: Given 2xy = k

Substituting this value of y in another curve equation i.e., 2x = y², we get

Taking cube root on both sides, we get

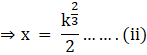
Substituting equation (ii) in equation (i), we get

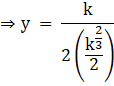
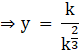
Hence the point of intersection of the two cures is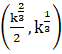

Now given 2x = y²

Differentiating this with respect to x, we get

Now finding the above differentiation value at the point of intersection i.e., at 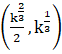, we get

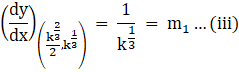
Also given 2xy = k

Differentiating this with respect to x, we get

Now applying the product rule of differentiation, we get

Now finding the above differentiation value at the point of intersection i.e., at 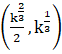, we get

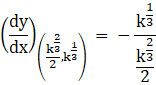
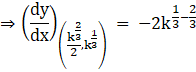
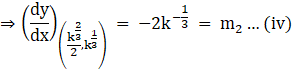
But the two curves intersect orthogonally, if

m₁.m₂ = -1

Now substituting the values from equation (iii) and equation (iv), we get

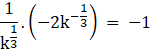
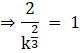
Taking cube on both sides we get

k² = 2³ = 8

⇒ k = 2√2

Hence this is the condition for the given two curves to intersect orthogonally.