Given: the curves y = 4–x² and y = x²

To find: the angle of intersection of the two curves

Explanation: consider first curve

y = 4–x²

Differentiating the above curve with respect to x we get

Consider second curve

y = x²

Differentiating the above curve with respect to x we get

Given y = x²

Substituting this in other curve equation, we get

x² = 4-x²

⇒ 2x² = 4

⇒ x² = 2

⇒ x = ±√2

When x = √2, we get

y = (√2)²⇒ y = 2

When x = -√2, we get

y = (-√2)²⇒ y = 2

Thus the points of intersection are (√2, 2) and (-√2, 2)

We know angle of intersection can be found by following formula,

i.e.,

Substituting the values from equation (i) and equation (ii), we get

For (√2, 2), the above equation becomes,

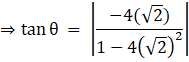
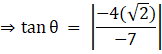
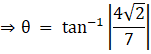
Hence the angle of intersection of the curves y = 4–x² and y = x² is