Show that the line 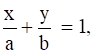 touches the curve
touches the curve ![]() at the point where the curve intersects the axis of y.
at the point where the curve intersects the axis of y.
Given: equation of line ![]() , the curve
, the curve ![]() intersects the y-axis
intersects the y-axis
To show: the line touches the curve at the point where the curve intersects the axis of y
Explanation: given the curve ![]() intersects the y-axis, i.e., at x = 0
intersects the y-axis, i.e., at x = 0
Now differentiate the given curve equation with respect to x, i.e.,
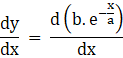
Taking out the constant term,
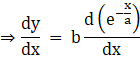
Now differentiating it we get
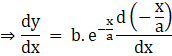
![]()
Now substitute x = 0, we get
![]()
![]()
![]()
Now consider line equation,
![]()
We will differentiate this with respect to x, we get
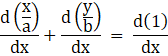
Taking out the constant terms, we get
![]()
![]()
![]()
Line touches the curve if there slopes are equal.
From equation (i) and (ii), we see that
m1 = m2
Hence the line touches the curve at the point where the curve intersects the axis of y.