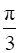Given: a right-angled triangle, such that sum of the lengths of its hypotenuse and side is given

To show: the area of the triangle is maximum when the angle between them is

Explanation:

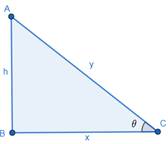
Let ΔABC be the right-angled triangle,

Let hypotenuse, AC = y,

side, BC = x, AB = h

Now sum of the side and hypotenuse is given,

⇒ x+y = k, where k is any constant value

⇒ y = k-x………..(i)

Now let A be the area of the triangle, then we know

Now applying the Pythagoras theorem, we get

y² = x²+h²

Now substituting equation (i) in above equation, we get

Now substituting the value from equation (iii) into equation (ii), we get

Now differentiating above equation with respect to x, we get

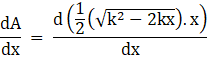
Now taking out the constant term we get

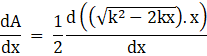
Now applying the product rule, we get

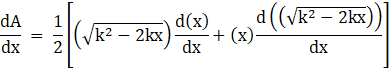
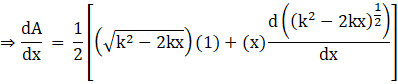
Applying the power rule of differentiation on second part in above equation, we get

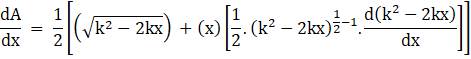
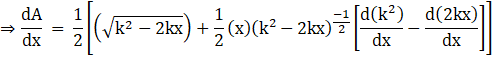
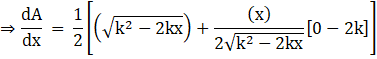
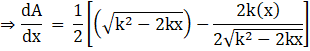
Now critical point is found by equating the first derivative to 0, i.e.,

⇒k²-2kx = kx

⇒k² = 2kx+kx

⇒ k² = 3kx

⇒ k = 3x

Again, differentiating equation (iv) with respect to x, we get

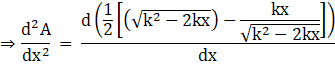
Taking out the constant term and taking the LCM, we get

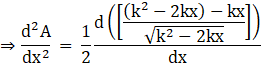
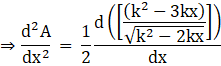
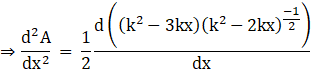
Applying the product rule of differentiation, we get

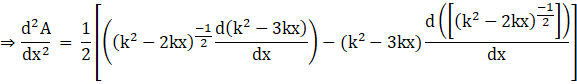
Now applying the power rule of differentiation, we get

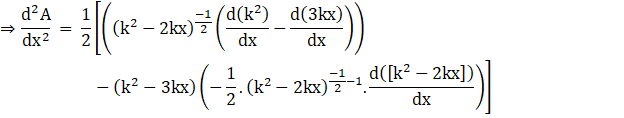
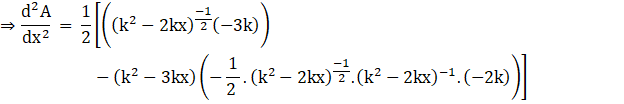
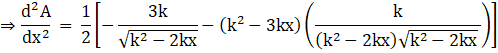
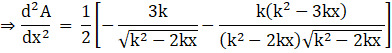
Substituting , in above equation, we get

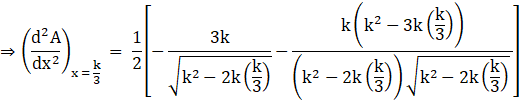
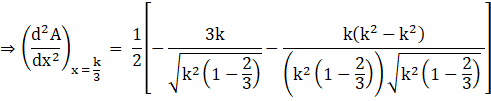
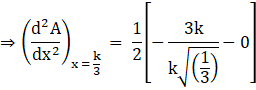
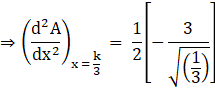
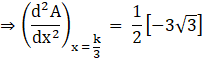
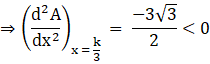
Hence the maximum value of A is at

We know,

Now from figure,

Substituting the value of y = k-x from equation (i), we get

Substituting the value of , we get

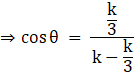
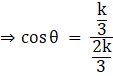
This is possible only when

Hence the area of the triangle is maximum only when the angle between them is