If the straight-line x cosα + y sinα = p touches the curve 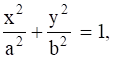 then prove that a2 cos2α + b2 sin2α = p2.
then prove that a2 cos2α + b2 sin2α = p2.
Given: equation of straight line x cosα + y sinα = p, equation of curve ![]() and the straight line touches the curve
and the straight line touches the curve
To prove: a2 cos2α + b2 sin2α = p2
Explanation: given equation of the line is
x cosα + y sinα = p
⇒ y sinα = p-x cosα
![]()
![]()
![]()
![]()
Comparing this with the equation y = mx+c we see that the slope and intercept of the given line is
![]() and
and ![]()
We know that, if a line y = mx+c touches the eclipse![]() , then required condition is
, then required condition is
c2 = a2m2+b2
Now substituting the corresponding values, we get
![]()
![]()
![]()
Cancelling the like terms we get
p2 = b2sin2α+a2cos2α
Hence proved
28