An open box with square base is to be made of a given quantity of card board of area c2. Show that the maximum volume of the box is 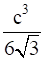 cubic units.
cubic units.
Given: an open box with square base is made out of a cardboard of c2 area
To show: the maximum volume of the box is ![]() cubic units.
cubic units.
Explanation:
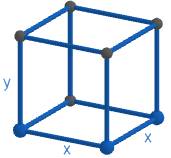
Let the side of the square be x cm and
Let the height the box be y cm.
Then area of the card board used is
A = area of square base + 4× area of rectangle
⇒ A = x2+4xy
But it is given this is equal to c2, hence
c2 = x2+4xy
⇒ 4xy = c2-x2
![]()
Then as per the given criteria the volume of the box with square base will be,
V = base×height
Here base is square, so volume becomes
V = x2y……(ii)
Now substituting equation (i) in equation (ii), we get
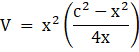
![]()
![]()
Now finding the first derivative of the volume, we get
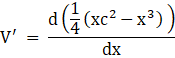
Taking out the constant terms, we get
![]()
Applying the sum rule of differentiation, we get
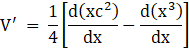
Taking out the constant terms, we get
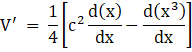
Applying the differentiation, we get
![]()
Now we will apply second derivative test to find out the maximum value of x, so for that let V’ = 0, so equating above equation with 0, we get
![]()
⇒ c2-3x2 = 0
⇒ 3x2 = c2
![]()
![]()
Differentiating equation (iii) again with respect to x, we get
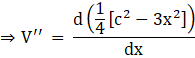
Taking out the constant terms, we get
![]()
Applying differentiation rule of sum, we get
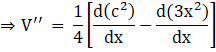
![]()
![]()
![]()
At ![]() , the above equation becomes,
, the above equation becomes,
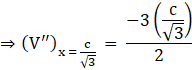
![]()
Thus the volume (V) is maximum at ![]()
∴ Maximum volume of the box is
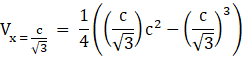
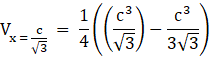
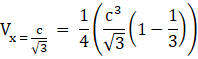
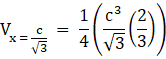
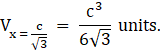
Hence the maximum volume of the box is ![]() cubic units.
cubic units.
Hence proved