Given: rectangle of perimeter 36cm

To find: the dimensions of the rectangle which will sweep out a volume as large as possible, when revolved about one of its sides. Also to find the maximum volume

Explanation: Let the length and the breadth of the rectangle be x and y.

Then it is given perimeter of the rectangle is 36cm,

⇒ 2x+2y = 36

⇒ x+y = 18

⇒ y = 18-x………(i)

Now when the rectangle revolve about side y it will form a cylinder with y as the height and x as the radius, then if the volume of the cylinder is V, then we know

V = πx²y

Substituting value from equation (i) in above equation we get

V = πx²(18-x)

⇒ V = π(18x²-x³)

Now we will find first derivative of the above equation, we get

Taking out the constant terms and applying the sum rule of differentiation, we get

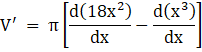
V' = π[18(2x)-3x² ]

V' = π[36x-3x² ]……(ii)

Now to find the critical point we will equate the first derivative to 0, i.e.,

V’ = 0

⇒ π(36x-3x²) = 0

⇒ 36x-3x² = 0

⇒ 36x = 3x²

⇒ 3x = 36

⇒ x = 12……..(iii)

Now we will find the second derivative of the volume equation, this can be done by again differentiating equation (ii), we get

Taking out the constant terms and applying the sum rule of differentiation, we get

V’’ = π[36-3(2x) ]

V’’ = π[36-6x]

Now substituting x = 12 (from equation (iii)), we get

V’’_{x = 12} = π[36-6(12)]

V’’_{x = 12} = π[36-72]

V’’_{x = 12} = -36π<0

Hence at x = 12, V will have maximum value.

The maximum value of V can be found by substituting x = 12 in V = π(18x²-x³), i.e.,

V_{x = 12} = π (18(12)²-(12)³)

V_{x = 12} = π (18(144)-(1728))

V_{x = 12} = π (2592-(1728))

V_{x = 12} = 864π cm³

Hence the dimensions of the rectangle which will sweep out a volume as large as possible, when revolved about one of its sides equal to 12cm.

And the maximum volume is 864π cm³.