Given the equation of the curve is

y (1 + x²) = 2 – x

Differentiating on both sides with respect to x, we get

Applying the power rule we get

We know derivative of a constant is 0, so above equation becomes

Applying the power rule we get

As the given curve passes through the x-axis, i.e., y=0,

So the equation on given curve becomes,

y(1+x²)=2-x

⇒ 0(1+x²)=2-x

⇒ 0=2-x

⇒ x=2

So the given curve passes through the point (2,0)

So the equation (i) at point (2,0) is,

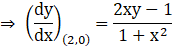
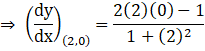
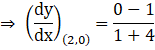
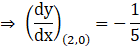
Hence, the slope of tangent to the curve is

Therefore, the equation of tangent of the curve passing through (2,0) is given by

⇒ 5y=-x+2

⇒ x+5y=2

So the equation of tangent to the curve y (1 + x²) = 2 – x, where it crosses x-axis is x+5y=2.

Therefore the correct option is option A.