Given the equation of the curve is

y = e^2x

Differentiating on both sides with respect to x, we get

Applying the exponential rule of differentiation, we get

As it is given the curve has tangent at (0,1), so the curve passes through the point (0,1), so above equation at (0,1), becomes

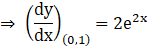
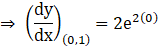
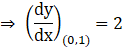
So, the slope of the tangent to the curve at point (0,1) is 2

Hence the equation of the tangent is given by

y-1=2(x-0)

⇒ y-1=2x

⇒ y=2x+1

It is given that the tangent to the curve y=e^2x at the point (0,1) meet x-axis i.e., y=0

So the equation on tangent becomes,

⇒ y=2x+1

⇒ 0=2x+1

⇒ 2x=-1

Hence the required point is

Therefore the tangent to the curve y = e^2x at the point (0, 1) meets x-axis at

So the correct option is option B.