Given equation of curve is x = t² + 3t – 8, y = 2t² – 2t – 5

x = t² + 3t – 8

Differentiating on both sides with respect to t, we get

Applying the sum rule of differentiation, we get

We know derivative of a constant is 0, so above equation becomes

Applying the power rule we get

y = 2t² – 2t – 5

Differentiating on both sides with respect to t, we get

Applying the sum rule of differentiation, we get

We know derivative of a constant is 0, so above equation becomes

Applying the power rule we get

Now we know,

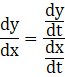
Now substituting the values from equation (i) and (ii), we get

As given the curve passes through the point (2,-1), substituting these values in given curve equation we get

x = t² + 3t – 8

⇒ 2= t² + 3t – 8

⇒ t² + 3t – 8-2=0

⇒ t² + 3t – 10=0

Splitting the middle term we get

⇒ t² + 5t-2t – 10=0

⇒ t(t+ 5) -2(t+5)=0

⇒ (t+ 5) (t-2)=0

⇒ t+5=0 or t-2=0

⇒ t=-5or t=2……….(iii)

y = 2t² – 2t – 5

⇒ -1=2t² – 2t – 5

⇒ 2t² – 2t – 5+1=0

⇒ 2t² – 2t – 4=0

Taking 2 common we get

⇒ t² – t – 2=0

Splitting the middle term we get

⇒ t² – 2t +t– 2=0

⇒ t(t– 2)+1(t– 2)=0

⇒ (t– 2)(t+1)=0

⇒ (t– 2)=0 or (t+1)=0

⇒ t=2 or t=-1……..(iv)

So from equation (iii) and (iv), we can see that 2 is common

So t=2

So the slope of the tangent at t=2 is given by

Therefore, the slope of tangent to the curve x = t² + 3t – 8, y = 2t² – 2t – 5 at the point (2, –1) is

So the correct option is option B.