The maximum value of 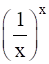 is:
is:
Let ![]() ………(i)
………(i)
Taking logarithm on both sides we get
![]()
![]()
Now applying first derivative, we get

Now applying the product rule of differentiation we get

Now applying the derivative we get
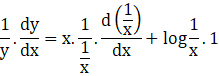

![]()
![]()
![]()
![]()
Substituting the value of y from equation (i), we get
![]()
Now we will find the critical point by equating equation (i) to 0, we get
![]()
![]() as
as ![]() cannot be equal to 0
cannot be equal to 0
![]()
But 1=log e1
![]()
Equating the terms we get
![]()
![]()
Hence f(x) has a stationary point at ![]() .
.
i.e the maximum value of ![]()
So the correct option is option C.
59