Fill in the blanks in each of the following
The least value of the function 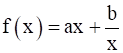 (a > 0, b > 0, x > 0) is ______.
(a > 0, b > 0, x > 0) is ______.
Given ![]() (a > 0, b > 0, x > 0)
(a > 0, b > 0, x > 0)
Now apply the derivative we get

Now applying the sum rule of differentiation we get

Now applying the quotient rule of differentiation on second part we get

![]()
![]()
We will equate this with 0 to get critical points,
f’(x)=0
![]()
![]()
![]()

Now second derivative gives,
Now apply the derivative we get

Now applying the sum rule of differentiation we get

Now applying the quotient rule of differentiation on second part we get

![]()
![]()
We will equate this with ![]() we get
we get



Thus the least value of f(x) is






Multiply and divide by ![]() , we get
, we get


Hence the least value of the function ![]() (a > 0, b > 0, x > 0) is
(a > 0, b > 0, x > 0) is ![]()
64