Prove that in any triangle ABC, 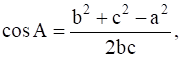where a, b, c are the magnitudes of the sides opposite to the vertices A, B, C, respectively

Given:


a, b, c are magnitudes of the sides opposite to the vertices A, B, C respectively.


⇒ AB = c, BC = a and CA = b


To Prove:


In triangle ABC,



Construction: We have constructed a triangle ABC and named the vertices according to the question.


Note the height of the triangle, BD.


If ∠BAD = A


Then, BD = c sin A


[∵ in ∆BAD



⇒ BD = c sin A]


And, AD = c cos A


[∵ in ∆BAD



⇒ AD = c cos A]



Proof:


Here, components of c which are:


c sin A


c cos A


are drawn on the diagram.


Using Pythagoras theorem which says that,


(hypotenuse)2 =(perpendicular)2 + (base)2


Take ∆BDC, which is a right-angled triangle.


Here,


Hypotenuse = BC


Base = CD


Perpendicular = BD


We get,


(BC)2 = (BD)2 + (CD)2


⇒ a2 = (c sin A)2 + (CD)2 [∵ from the diagram, BD = c sin A]


⇒ a2 = c2 sin2 A + (b – c cos A)2


[∵ from the diagram, AC = CD + AD


⇒ CD = AC – AD


⇒ CD = b – c cos A]


⇒ a2 = c2 sin2 A + (b2 + (-c cos A)2 – 2bc cos A) [∵ from algebraic identity, (a – b)2 = a2 + b2 – 2ab]


⇒ a2 = c2 sin2 A + b2 + c2 cos2 A – 2bc cos A


⇒ a2 = c2 sin2 A + c2 cos2 A + b2 – 2bc cos A


⇒ a2 = c2 (sin2 A + cos2 A) + b2 – 2bc cos A


⇒ a2 = c2 + b2 – 2bc cos A [∵ from trigonometric identity, sin2 θ + cos2 θ = 1]


⇒ 2bc cos A = c2 + b2 – a2


⇒ 2bc cos A = b2 + c2 – a2



Hence, proved.


15