Integrate the function: 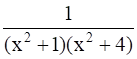
Given: ![]()
![]()
Using partial differentiation:
![]()
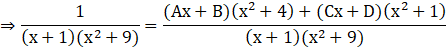
⇒1 = (Ax + B)(x2 + 4)+(Cx + D)(x2 + 1)
⇒ 1 = Ax3 +4Ax+ Bx2 + 4B+ Cx3 + Cx + Dx2 + D
⇒ 1 = (A+C)x3 +(B+D)x2 +(4A+C)x + (4B+D)
Equating the coefficients of x, x2, x3 and constant value. We get:
(a) A + C = 0 ⇒ C = -A
(b) B + D = 0 ⇒ B = -D
( c) 4A + C =0 ⇒ 4A = -C ⇒ 4A = A ⇒ 3A = 0 ⇒ A = 0 ⇒ C = 0
( d) 4B + D = 1 ⇒ 4B – B = 1 ⇒ B = 1/3 ⇒ D = -1/3
Put these values in equation (1)
![]()
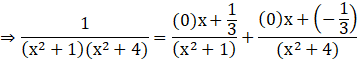
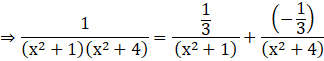
![]()
![]()
![]()
![]()
15