Integrate the function: 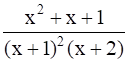
Given: ![]()
Let![]()
Using partial differentiation:
let![]()
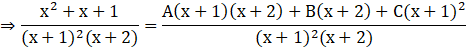
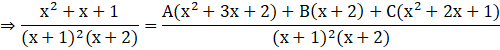
⇒ x2 + x + 1 = Ax2 + 3Ax + 2A + Bx +2B + Cx2 + 2Cx + C
⇒ x2 + x + 1 = (2A+2B+C) + (3A+B+2C)x + (A+C)x2
Equating the coefficients of x, x2 and constant value. We get:
(a) A + C = 1
(b) 3A + B + 2C = 1
( c) 2A+2B+C =1
After solving we get:
A=-2, B=1 and C=3
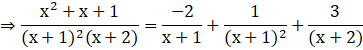
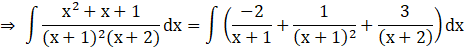
![]()
![]()
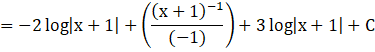
![]()
22