Book: RS Aggarwal - Mathematics
Chapter: 3. Functions
Subject: Maths - Class 11th
Q. No. 1 of Exercise 3C
Listen NCERT Audio Books to boost your productivity and retention power by 2X.
Find the domain of each of the following real function.
(i)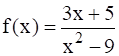 
(ii)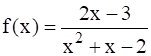 
(iii)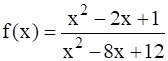 
(iv)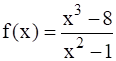 
(i)
Given: 
Need to find: Where the functions are defined.
To find the domain of the function f(x) we need to equate the denominator to 0.
Therefore,
⇒ 
⇒ 
It means that the denominator is zero when x = 3 and x = -3
So, the domain of the function is the set of all the real numbers except +3 and -3.
The domain of the function, Df(x) = (- ∞, -3) ∪ (-3, 3) ∪ (3, ∞).
(ii)
Given: 
Need to find: Where the functions are defined.
To find the domain of the function f(x) we need to equate the denominator to 0.
Therefore,
⇒ 
⇒ 
⇒ 
⇒ 
& 
It means that the denominator is zero when x = 1 and x = -2
So, the domain of the function is the set of all the real numbers except 1 and -2.
The domain of the function, Df(x) = (- ∞, -2) ∪ (-2, 1) ∪ (1, ∞).
(iii)
Given: 
Need to find: Where the functions are defined.
To find the domain of the function f(x) we need to equate the denominator to 0.
Therefore,
⇒ 
⇒ 
⇒ 
⇒ 
& 
It means that the denominator is zero when x = 2 and x = 6
So, the domain of the function is the set of all the real numbers except 2 and 6.
The domain of the function, Df(x) = (- ∞, 2) ∪ (2, 6) ∪ (6, ∞).
(iv)
Given: 
Need to find: Where the functions are defined.
To find the domain of the function f(x) we need to equate the denominator to 0.
Therefore,
⇒ 
⇒ 
It means that the denominator is zero when x = -1 and x = 1
So, the domain of the function is the set of all the real numbers except -1 and +1.
The domain of the function, Df(x) = (- ∞, -1) ∪ (-1, 1) ∪ (1, ∞).
