Book: RS Aggarwal - Mathematics
Chapter: 3. Functions
Subject: Maths - Class 11th
Q. No. 13 of Exercise 3C
Listen NCERT Audio Books to boost your productivity and retention power by 2X.
Find the domain and the range of each of the following real function: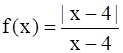 
Given: 
Need to find: Where the functions are defined.
To find the domain of the function f(x) we need to equate the denominator of the function to 0.
Therefore,
x – 4 = 0
⇒ x = 4
It means that the denominator is zero when x = 4
So, the domain of the function is the set of all the real numbers except 4.
The domain of the function, Df(x) = (- ∞, 4) ∪ (4, ∞).
The numerator is an absolute function of the denominator. So, for any value of x from the domain set, we always get either +1 or -1 as the output. So, the range of the function is a set containing -1 and +1
Therefore, the range of the function, Rf(x) = { -1 , 1 }
