Find the domain and the range of the cube root function,
f: R → R: f(x) = x1/3 for all x ϵ R. Also, draw its graph.
Given:
f(x) = x1/3∀ x є R
To Find: Domain and range of the given function.
Here, f(x) = x1/3
The domain of the above function would be,
Domain(f) = (-∞, ∞) {x | x є R}
Because all real numbers have a cube root. There is no value of x which makes the function undefined.
Now, to find the range
Consider f(x) = y
Then, y = x1/3
y3 = x
Since f(x) is continuous, it follows that
Range(f) = (-∞, ∞) {y | y є R}
Because for every value of y there would be a cube of that value.
Graph:
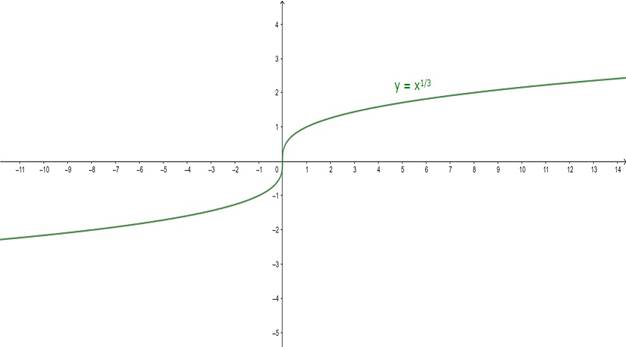
1