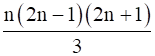
To Prove:

1² + 3² + 5² + 7² + … + (2n – 1)² =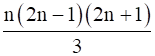

Steps to prove by mathematical induction:

Let P(n) be a statement involving the natural number n such that

(i) P(1) is true

(ii) P(k + 1) is true, whenever P(k) is true

Then P(n) is true for all n ϵ N

Therefore,

Let P(n): 1² + 3² + 5² + 7² + … + (2n – 1)² =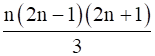

Step 1:

P(1) = = 1

Therefore, P(1) is true

Step 2:

Let P(k) is true Then,

P(k): 1² + 3² + 5² + 7² + … + (2k – 1)² =

Now,

1² + 3² + 5² + 7² + … + (2(k + 1)–1)² =

=

=

=

=

= (Splitting the middle term)

⁼

= P(k + 1)

Hence, P(k + 1) is true whenever P(k) is true

Hence, by the principle of mathematical induction, we have

1² + 3² + 5² + 7² + … + (2n – 1)² = for all n ϵ N