Using the principle of mathematical induction, prove each of the following for all n ϵ N:
3.22 + 32.23 + 33.24 + …. + 3n.2n+1 =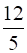 (6n – 1).
(6n – 1).
To Prove:
![]()
Let us prove this question by principle of mathematical induction (PMI)
Let P(n): ![]()
For n = 1
LHS = ![]() = 12
= 12
RHS = ![]()
= ![]() = 12
= 12
Hence, LHS = RHS
P(n) is true for n = 1
Assume P(k) is true
![]() ……(1)
……(1)
We will prove that P(k + 1) is true
![]()
![]()
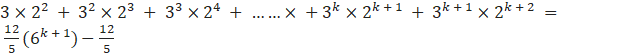 …(2)
…(2)
We have to prove P(k + 1) from P(k) ie (2) from (1)
From (1)
![]()
Adding ![]() both sides
both sides
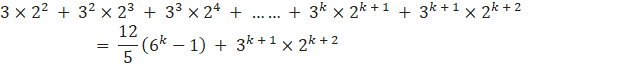
![]()
![]()
![]()
![]()
![]()
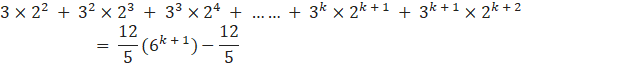
which is the same as P(k + 1)
Therefore, P (k + 1) is true whenever P(k) is true.
By the principle of mathematical induction, P(n) is true for×
where n is a natural number
Put k = n - 1
![]()
![]()
Hence proved
1