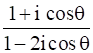Since is purely real

Firstly, we need to solve the given equation and then take the imaginary part as 0

We rationalize the above by multiply and divide by the conjugate of (1 -2i cos θ)

We know that,

(a – b)(a + b) = (a² – b²)

[∵ i² = -1]

Since is purely real [given]

Hence, imaginary part is equal to 0

i.e.

⇒ 3 cos θ = 0 × (1 + 4 cos²θ)

⇒ 3 cos θ = 0

⇒ cos θ = 0

⇒ cos θ = cos 0

Since, cos θ = cos y

Then where n Є Z

Putting y = 0

where n Є Z

Hence, for is purely real.