If 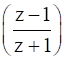 is purely an imaginary number and z ≠ -1 then find the value of |z|.
is purely an imaginary number and z ≠ -1 then find the value of |z|.
Given: ![]() is purely imaginary number
is purely imaginary number
Let z = x + iy
So, ![]()
![]()
Now, rationalizing the above by multiply and divide by the conjugate of [(x + 1) + iy]
![]()
![]()
Using (a – b)(a + b) = (a2 – b2)
![]()
![]()
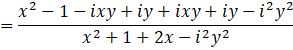
Putting i2 = -1
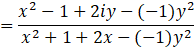
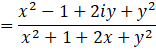
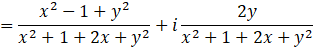
Since, the number is purely imaginary it means real part is 0
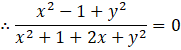
⇒ x2 + y2 – 1 = 0
⇒ x2 + y2 = 1
![]()
![]()
∴ |z| = 1
1