If (x + iy)1/3 = (a + ib) then prove that 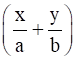 = 4 (a2 – b2).
= 4 (a2 – b2).
Given that, (x + iy)1/3 = (a + ib)
⇒ (x + iy) = (a + ib)3
⇒ (a + ib)3 = x + iy
⇒ a3 + (ib)3 + 3a2ib + 3ai2b2 = x + iy
⇒ a3 - ib3 + 3a2ib - 3ab2 = x + iy
⇒ a3 - 3ab2 + i(3a2b - b3) = x + iy
On equating real and imaginary parts, we get
x = a3 - 3ab2 and y = 3a2b - b3
Now , ![]()
![]()
= a2 - 3b2 + 3a2 - b2
= 4a2 - 4b2
= 4(a2 - b2)
Hence, ![]()
1