Given: A = {0, 1, 2} and B = {3, 5, 7, 9}

f = {(x, y): x ∈ A, y ∈ B and y = 2x + 3}

For x = 0

y = 2x + 3

y = 2(0) + 3

y = 3 ∈ B

For x = 1

y = 2x + 3

y = 2(1) + 3

y = 5 ∈ B

For x = 2

y = 2x + 3

y = 2(2) + 3

y = 7 ∈ B

∴ f = {(0, 3), (1, 5), (2, 7)}

(0, 5), (0, 7), (0, 9), (1, 3), (1, 7), (1, 9), (2, 3), (2, 5), (2, 9) are not the members of ‘f’ because they are not satisfying the given condition y = 2x + 3

Now, we have to show that f is a function from A to B

Function:

(i) all elements of the first set are associated with the elements of the second set.

(ii) An element of the first set has a unique image in the second set.

f = {(0, 3), (1, 5), (2, 7)}

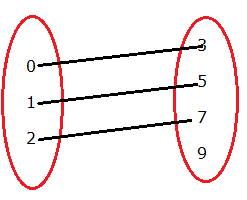
Here, (i) all elements of set A are associated with an element in set B.

(ii) an element of set A is associated with a unique element in set B.

∴ f is a function.

Dom (f) = 0, 1, 2

Range (f) = 3, 5, 7