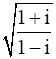
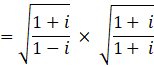
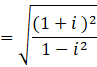
Let

Now, separating real and complex part , we get

……….eq.1

…………eq.2

Squaring and adding eq.1 and eq.2, we get

1 = r²

Since r is always a positive no., therefore,

r = 1,

hence its modulus is 1.

now , dividing eq.2 by eq.1 , we get,

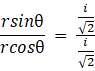
tanθ = 1

Since , and tanθ =1. therefore the θ lies in first quadrant.

Tanθ = 1, therefore

Representing the complex no. in its polar form will be

}