Solve each of the following in equations and represent the solution set on the number line.
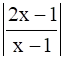 < 2, x ϵ R.
< 2, x ϵ R.
Given:
![]() < 2, x ϵ R.
< 2, x ϵ R.
-2 < ![]() < 2
< 2
![]() > -2 and
> -2 and ![]() < 2
< 2
When,
![]() > -2
> -2
Adding 2 to both sides in the above equation
![]() + 2 > -2 + 2
+ 2 > -2 + 2
![]() > 0
> 0
![]() > 0
> 0
![]() > 0
> 0
Signs of 4x – 3:
4x – 3 = 0 → ![]()
(Adding 3 to both sides and then dividing both sides by 4)
4x – 3 > 0 → ![]()
(Adding 3 to both sides and then dividing both sides by 4)
4x – 3 < 0 → ![]()
(Adding 3 to both sides and then dividing both sides by 4)
Signs of x – 1:
x – 1 = 0 → x = 1 (Adding 1 to both the sides)
x – 1 > 0 → x > 1 (Adding 1 to both the sides)
x – 1 < 0 → x < 1 (Adding 1 to both the sides)
At x = 1, ![]() is not defined.
is not defined.
Intervals that satisfy the required condition: > 0
![]() or x > 1
or x > 1
Now, when ![]() < 2
< 2
Subtracting 2 from both the sides
![]() -2 < 2 -2
-2 < 2 -2
![]() < 0
< 0
![]() < 0
< 0
![]() < 0
< 0
Signs of x – 1:
x – 1 = 0 → x = 1 (Adding 1 on both the sides)
x – 1 < 0 → x < 1 (Adding 1 on both the sides)
x – 1 > 0 → x > 1 (Adding 1 on both the sides)
At x = 1, ![]() is not defined
is not defined
Interval which satisfy the required condition: < 0
x < 1
Now, combining the intervals:
![]() or x > 1 and x <1
or x > 1 and x <1
Merging the overlapping intervals:
![]()
Therefore,
![]()