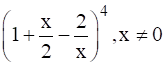
To find: Expansion of

Formula used: (i)

(ii) (a+b)ⁿ =   ⁿC₀aⁿ + ⁿC₁a^n-1b + ⁿC₂a^n-2b² + …… +ⁿC_n-1ab^n-1 + ⁿC_nbⁿ

We have,

Let = a and = b … (i)

Now the equation becomes (a + b)⁴

(Substituting value of b from eqn. i )

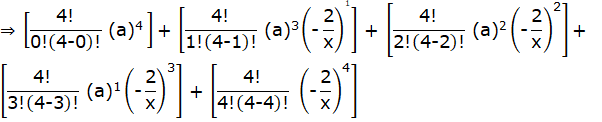
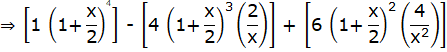
(Substituting value of a from eqn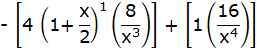. i )

…(ii)

We need the value of a⁴,a³ and a², where a =

For , Applying Binomial theorem

=

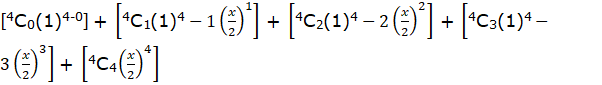
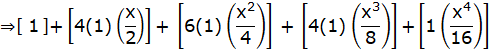
On rearranging the above eqn.

We have, = + x³ + x² + 2x + 1

For, (a+b)³ , we have formula a³+b³+3a²b+3ab²

For, , substituting a = 1 and b = in the above formula

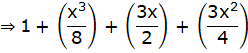
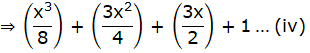
For, (a+b)² , we have formula a²+2ab+b²

For, , substituting a = 1 and b = in the above formula

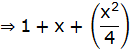
… (v)

Putting the value obtained from eqn. (iii),(iv) and (v) in eqn. (ii)

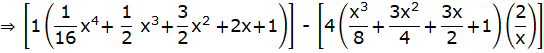
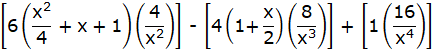
On rearranging

Ans) + + - +