If a, b, c are in AP, prove that
(i) (a – c)2 = 4(a – b)(b – c)
(ii) a2 + c2 + 4ac = 2(ab + bc + ca)
(iii) a3 + c3 + 6abc = 8b3
(i) (a – c)2 = 4(a – b)(b – c)
To prove: (a – c)2 = 4(a – b)(b – c)
Given: a, b, c are in A.P.
Proof: Since a, b, c are in A.P.
⇒ c – b = b – a = common difference
⇒ b – c = a – b … (i)
And, 2b = a + c (a, b, c are in A.P.)
⇒ 2b – c = a … (ii)
Taking LHS = (a – c)2
= ( 2b – c – c )2 [from eqn. (ii)]
= ( 2b – 2c )2
= 4( b – c )2
= 4( b – c ) ( b – c )
= 4( a – b ) ( b – c ) [b–c = a–b from eqn. (i)]
= RHS
Hence Proved
(ii) a2 + c2 + 4ac = 2(ab + bc + ca)
To prove: a2 + c2 + 4ac = 2(ab + bc + ca)
Given: a, b, c are in A.P.
Proof: Since a, b, c are in A.P.
⇒ 2b = a + c
![]() … (i)
… (i)
Taking RHS = 2(ab + bc + ca)
Substituting value of b from eqn. (i)
![]()
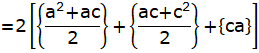
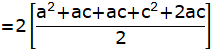
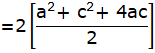
= a2 + c2 + 4ac
= LHS
Hence Proved
(iii) a3 + c3 + 6abc = 8b3
To prove: a3 + c3 + 6abc = 8b3
Given: a, b, c are in A.P.
Formula used: (a+b)3 = a3 + 3ab(a+b) + b3
Proof: Since a, b, c are in A.P.
⇒ 2b = a + c … (i)
Cubing both side,
![]()
⇒ 8b3 = a3 + 3ac(a+c) + c3
⇒ 8b3 = a3 + 3ac(2b) + c3 [a+c = 2b from eqn. (i)]
⇒ 8b3 = a3 + 6abc + c3
On rearranging,
a3 + c3 + 6abc = 8b3
Hence Proved