Evaluate :
NOTE:In an expression like this ⇒ 
, n represents the upper limit, 1 represents the lower limit , x is the variable expression which we are finding out the sum of and i represents the index of summarization.
(i)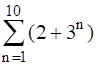 
(ii)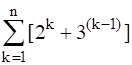 
(iii) 
We can write this as (2 + 31)+(2+32) + (2 +33)+… to 10 terms
= ( 2+2+2+… to 10 terms) + ( 3+32+33+… to 10 terms)
= 2×10 + (3+32+33+… to 10 terms)
= 20 + (3+32+33+… to 10 terms)
Sum of a G.P. series is represented by the formula, 
, when r≠1. ‘Sn’ represents the sum of the G.P. series upto nth terms, ‘a’ represents the first term, ‘r’ represents the common ratio and ‘n’ represents the number of terms.
Here,
a = 3
r =(ratio between the n term and n-1 term) 3
n = 10 terms
⇒
⇒
⇒
Thus, sum of the given expression is
= 20 + (3+32+33+… to 10 terms)
= 20 + 88572
=88592
(ii) The given expression can be written as,
( 21 + 31-1) + (22 + 32-1) + …to n terms
= (2 + 30) + ( 22+ 31) + …to n terms
= (2 + 1) +(22 + 3 ) + …to n terms
= (2 + 22 + …to 
terms) + ( 1 + 3 + … to 
terms)
Sum of a G.P. series is represented by the formula, 
, when r≠1. ‘Sn’ represents the sum of the G.P. series upto nth terms, ‘a’ represents the first term, ‘r’ represents the common ratio and ‘n’ represents the number of terms.
Here,
a = 2, 1
r = (ratio between the n term and n-1 term)2, 3
terms
⇒
⇒
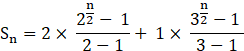
(iii) We can rewrite the given expression as
( 51 + 52 + 53+ …to 8 terms)
Sum of a G.P. series is represented by the formula, 
, when r>1. ‘Sn’ represents the sum of the G.P. series upto nth terms, ‘a’ represents the first term, ‘r’ represents the common ratio and ‘n’ represents the number of terms.
Here,
a = 5
r =(ratio between the n term and n-1 term) 5
n = 8 terms
⇒
⇒
⇒